【知识点】一些数论
- 数论函数,积性函数
陪域:包含值域的任意集合
数论函数:定义域为正整数,陪域为复数的函数
积性函数:对于任意互质的整数 a,b 有 f(ab) = f(a)f(b) .
完全积性函数:对于任意整数 a,b 有 f(ab) = f(a)f(b) .
φ(欧拉函数,计算与n互质的正整数之数目)
μ(莫比乌斯函数,关于非平方数的质因子数目)
σ(n的所有正因子之和)
d(n的正因子数目)
ϵ(定义为:若n = 1,ε(n)=1;若 n > 1,ε(n)=0。别称为“对于狄利克雷卷积的乘法单位”)
I(不变的函数,定义为 1(n) = 1)
id(单位函数,定义为 Id(n) = n)
- 狄利克雷卷积
设 f, g 是两个数论函数,设 h= f ∗ g , 它们的狄利克雷卷积是: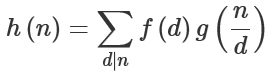
性质:满足交换律,结合律,分配率,(若均为积性函数,卷积也为积性函数)
单位元:ϵ
结合狄利克雷卷积得到的几个性质:
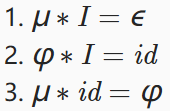


 浙公网安备 33010602011771号
浙公网安备 33010602011771号