【栈与队列】:基础实战篇
前言
一文带你了解栈与队列的基础,并且其经常考察的思维算法。本文用于记录自己的学习过程,同时向大家进行分享相关的内容。本文内容参考于 代码随想录 同时包含了自己的许多学习思考过程,如果有错误的地方欢迎批评指正!
栈与队列的技术理论
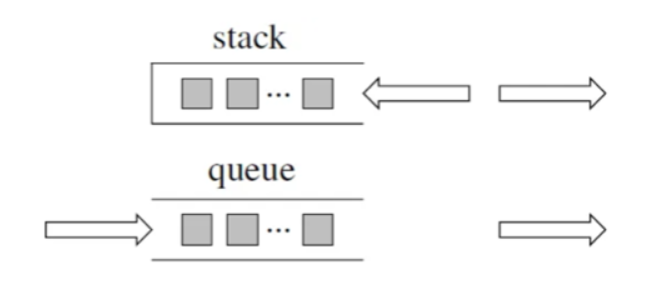
关于如何认识栈与队列,大家其实只有记住其最根本的就是两者的特性即不同,栈是后进先出,队列是先进先出。什么意思呢?就是对于栈结构,我们只能从一端(称之为栈顶)进行数据的插入和删除操作,所以先进入的数据就会到达栈的底部,每次弹出数据都是从栈顶弹出。那么队列呢就是,我们从队尾进行数据的插入操作,从队首进行数据的弹出删除操作。
栈的应用:我们主要是表达式求值,回溯递归中经常会用到。
队列的应用:进程相关调度,BFS算法,缓冲区打印经常会用到。
栈与队列的实战应用
栈的经典题目
有效的括号

相关技巧:其实这就是很经典的栈应用了,为什么?因为我们的每个左括号和相应的右括号一定是对应的。所以当我们遇到左括号的时候就压入栈中,遇到右括号就弹出栈顶的括号,看两者是否是相匹配的。所以这道题就很简单了,就是很简单的栈的应用。但是我们想,设计的时候,遇到左括号就进栈,那出栈的时候比较,该怎么评判二者是对应的括号呢?所以这里我们可以在左括号进栈的时候直接进其右括号,出栈直接比较其是否相等即可。
class Solution:
def isValid(self, s: str) -> bool:
ls=list(s)
tmp=[]
for i in range(len(s)):
if ls[i]=='(' :
tmp.append(')')
elif ls[i]=='{':
tmp.append('}')
elif ls[i]=='[':
tmp.append(']')
elif not tmp or tmp[-1]!=ls[i]:
return False
else:
tmp.pop()
return True if not tmp else False
删除字符串中重复相邻项
1047. 删除字符串中的所有相邻重复项 - 力扣(LeetCode)

相关技巧:思想很简单,同样也是栈的经典应用,遍历全部元素若栈非空直接比较栈顶元素是否相等,相等弹出栈顶元素,继续取下个元素,若不相等直接进栈,直至遍历完全部的元素。
class Solution:
def removeDuplicates(self, s: str) -> str:
stack=[]
for item in s:
if not stack or stack[-1]!=item:
stack.append(item)
elif stack[-1]==item:
stack.pop()
return ''.join(stack)
逆波兰表达式求值

相关技巧:首先我们要知道什么是逆波兰表达式。其实很简单,就是数字在前,运算符号在后。怎么理解去用栈呢?就是遇到操作数就压入栈中,遇到运算符号,取出栈顶两个操作数进行运算,结果在压入栈中,直至结束得到最终的结果。我们这里引入了运算符并定义了整数除法的取零方式,然后操作就按照刚才所述进行。
from operator import add, sub, mul
def div(x, y):
# 使用整数除法的向零取整方式
return int(x / y) if x * y > 0 else -(abs(x) // abs(y))
class Solution(object):
op_map = {'+': add, '-': sub, '*': mul, '/': div}
def evalRPN(self, tokens: List[str]) -> int:
stack = []
for token in tokens:
if token not in {'+', '-', '*', '/'}:
stack.append(int(token))
else:
op2 = stack.pop()
op1 = stack.pop()
stack.append(self.op_map[token](op1, op2)) # 第一个出来的在运算符后面
return stack.pop()
队列的经典题目
滑动窗口最大值

相关技巧:其实暴力法很简单直接两个for循环一套,时间复杂度为O($n*k$)。当然我们肯定不会这么去求解,精益求精。怎么做,首先思考其方式,滑动窗口一个一个往后移,返回窗口中的最大值,其滑动窗口的移动是不是有点类似于队列的方式,窗口每往后面移动一位,最先进的就出窗口,新来的就进入窗口。其实就是队列的特性,好了重点来了,我们可以用队列来模拟其轨迹,但是怎么返回其最大值呢?其实我们只需要让最大值和可能成为最大值的留在队列中即可。具体如何实现呢,就是进入一个元素就与其队列中的元素从后往前进行比较,比队列中的大,就将队列中的弹出,一直比到空或者小为值,就加入队列中。那窗口滑动过去了,怎么判断是否是最大的元素要弹出呢?就是比较其是否与最大元素相等,相等即弹出。具体实现代码如下
from collections import deque
class MyQueue: #单调队列(从大到小
def __init__(self):
self.queue = deque() #这里需要使用deque实现单调队列,直接使用list会超时
#每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
#同时pop之前判断队列当前是否为空。
def pop(self, value):
if self.queue and value == self.queue[0]:
self.queue.popleft()#list.pop()时间复杂度为O(n),这里需要使用collections.deque()
#如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
#这样就保持了队列里的数值是单调从大到小的了。
def push(self, value):
while self.queue and value > self.queue[-1]:
self.queue.pop()
self.queue.append(value)
#查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
def front(self):
return self.queue[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
result = []
for i in range(k): #先将前k的元素放进队列
que.push(nums[i])
result.append(que.front()) #result 记录前k的元素的最大值
for i in range(k, len(nums)):
que.pop(nums[i - k]) #滑动窗口移除最前面元素
que.push(nums[i]) #滑动窗口前加入最后面的元素
result.append(que.front()) #记录对应的最大值
return result
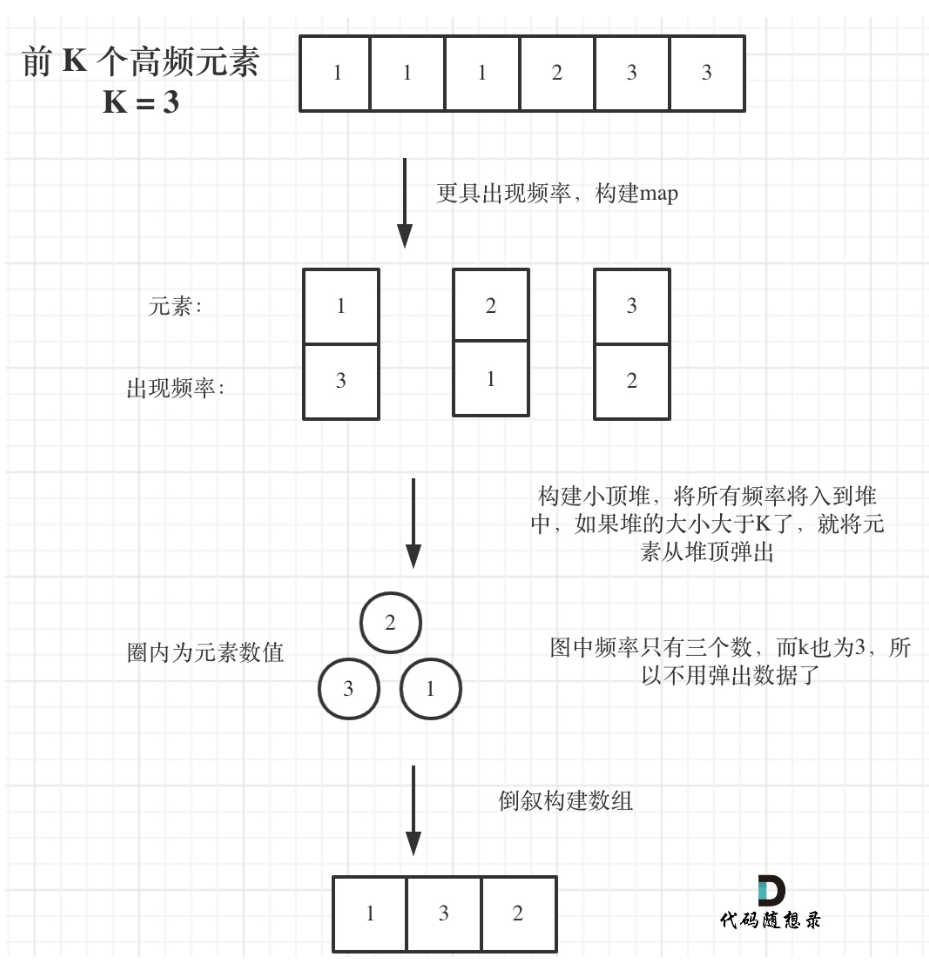
前 K 个高频元素

相关技巧:统计前k个频率高的元素,一看到统计频率其实我就应该想到构建map,然后根据map的出现的频率构建小根堆即可,当个数超过k,就弹出最小的,继续构建新的小根堆。
#时间复杂度:O(nlogk)
#空间复杂度:O(n)
import heapq
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
#要统计元素出现频率
map_ = {} #nums[i]:对应出现的次数
for i in range(len(nums)):
map_[nums[i]] = map_.get(nums[i], 0) + 1
#对频率排序
#定义一个小顶堆,大小为k
pri_que = [] #小顶堆
#用固定大小为k的小顶堆,扫描所有频率的数值
for key, freq in map_.items():
heapq.heappush(pri_que, (freq, key))
if len(pri_que) > k: #如果堆的大小大于了K,则队列弹出,保证堆的大小一直为k
heapq.heappop(pri_que)
#找出前K个高频元素,因为小顶堆先弹出的是最小的,所以倒序来输出到数组
result = [0] * k
for i in range(k-1, -1, -1):
result[i] = heapq.heappop(pri_que)[1]
return result
算法基础系列
一文了解什么是数组及其经典考察题目
走进链表及其经典考察题目
还不知道什么是哈希表,看这篇文章就够了
字符串匹配究极大招【KMP】:带你一步步从原理到构建


 浙公网安备 33010602011771号
浙公网安备 33010602011771号