Splay

prologue

快 csps 了还什么也不会的一条费鱼。 on 23.10.9

upd on 23.10.10：新增了内存回收技巧还有递归建树方式，并且重新维护了一下整篇文章。

下面是分别通过 acwing y总和樱雪喵学到的splay。

introduction

首先来了解一下二叉搜索树。二叉搜索树是一种二叉树的树形数据结构，其定义如下：

空树是二叉搜索树。
若二叉搜索树的左子树不为空，则其左子树上所有点的附加权值均小于其根节点的值。
若二叉搜索树的右子树不为空，则其右子树上所有点的附加权值均大于其根节点的值。
二叉搜索树的左右子树均为二叉搜索树。

下面是我画出来的一棵二叉搜索树，很显然是满足上述性质的（注意，图上的点都是表示点权）。

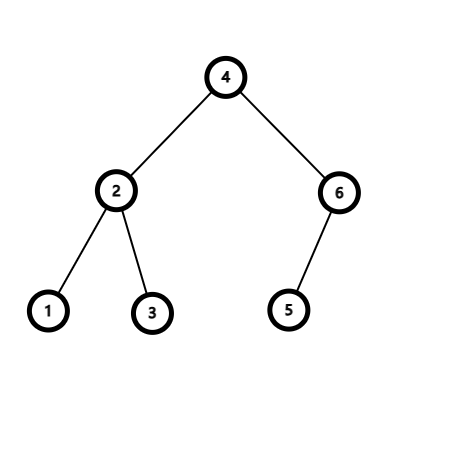
插入节点

我们如果要插入一个节点，应该遵循上面的规则，这样才能保证这个二叉搜索树的结构是一直保持的：

如果比当前节点的权值大，则向这个节点的右子树遍历。直到叶子节点然后停止，插入该值。
如果比当前节点的权值小，则向这个节点的左子树遍历。直到叶子节点然后停止，插入该值。
如果和当前节点的权值相同，则可以考虑两种方案：
- 直接在这个节点的下面进行连接。
- 给这个权值的节点开一个维度 cnt，用来统计这个权值的个数。

从理论与结构来说，第一种明显是荒谬之谈，但是第一种往往在实际过程中会比第二种少很多的情况特判，操作起来上手舒服。（或许这就是为什么大部分学校把信息学归为工科的原因？）

删除节点

我们删除节点的操作往往会比较麻烦：

如果这个节点没有子树，则我们可以直接删除。
如果只有一个儿子，直接将这个儿子和它的父节点相连，然后删除这个点。（图解）
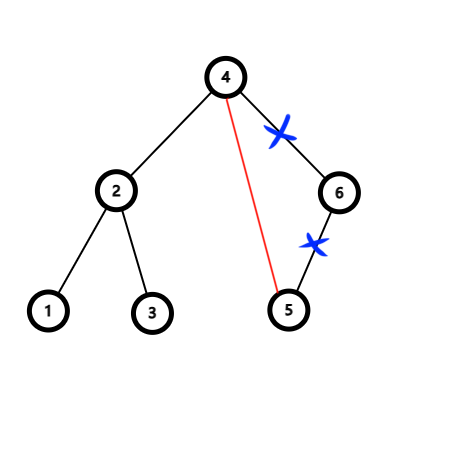
如果有两个儿子，那么我们删除的过程就会变得比较麻烦。（下面为重建的新图）
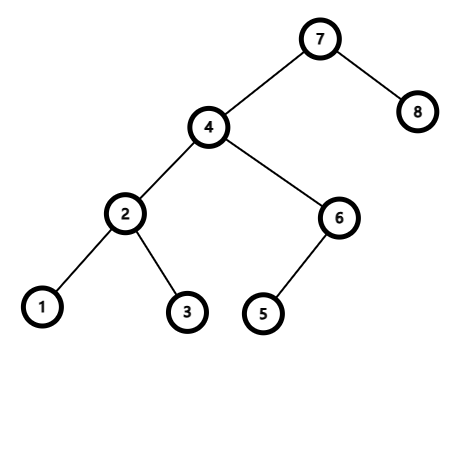
- 删除 4 号节点。我们首先先将与 4 相连的边都删掉
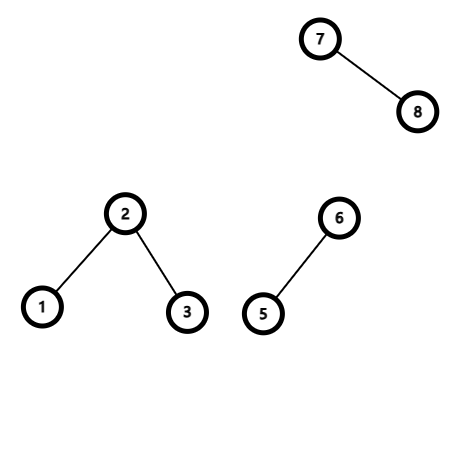
- 然后我们用一边的儿子（任意都可，看你习惯，我来左边）与原来的父节点相连。
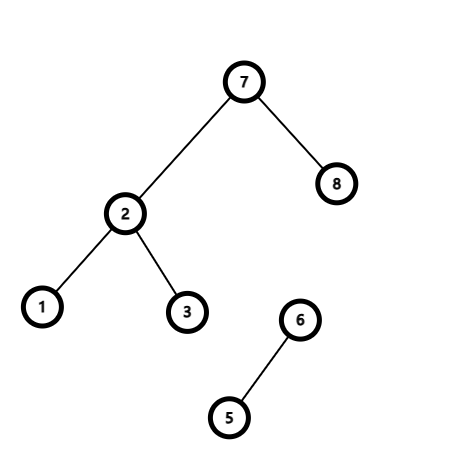
- 然后我们再按照搜索二叉树的原则，把右儿子给连接上。（图丑轻喷）

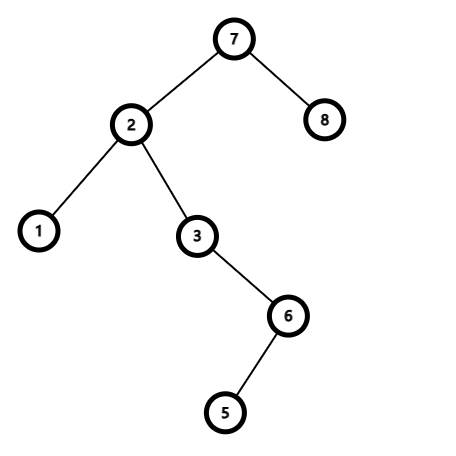
这里我们就成功的删除了 4 号节点，并且同时维护了搜索二叉树的性质。

我们对于一个节点的查询是和这个搜索二叉树的树高有关系的。

但是我们其实可以很轻松的构造一种方案，让这个效率降成 \(O(n)\) 了，就是从根节点开始不断加比它大的数，这样子我们的树高就是点的个数，我们的效率也就低了下来。

为了让我们的时间复杂度有保证，我们就诞生了平衡树这一种数据结构。通过左旋（zag）和右旋（zig）来维护搜索二叉树的树高一直为 \(log_2 n\) 的。

splay

zag & zig

首先我们得介绍清楚 zig 和 zag 的实现原理，否则后期难以进行。下面是摘自 oiwiki 上的图片。
左边通过右旋得到了右边，右边通过左旋得到了左边。

下面是对于左右旋的一个略详解：

右旋：将 \(A\) 的左孩子 \(B\) 向左上旋转，代替 \(A\) 成为根节点，将 \(A\) 结点向右下旋转成为 \(B\) 的右子树的根结点，\(B\) 的原来的右子树变为 \(A\) 的左子树。

左旋则是右旋的镜像操作。

（想了想还是把代码放在这里吧）

由于我们上面的左旋右旋都只和 x 是父亲的哪个儿子进行的方向进行判断。造作完成后，我们要更新节点的 size 信息。

这个 rotate 函数不断维护的过程可以抽相成无向边。从儿子到父亲的信息要更新，从父亲到儿子的信息也要更新，这样子才能算是成功旋转。

#define ll int

inline void rotate(ll x)
{
    ll y = fa(x), z = fa(y); bool c = get(x);
    fa(tr[x].s[c ^ 1]) = y, tr[y].s[c] = tr[x].s[c ^ 1]; // 断 x 的另一棵子树。
    tr[x].s[c ^ 1] = y, fa(y) = x, fa(x) = z; // 把 y 挂在自己下面
    if(z) tr[z].s[y == rs(z)] = x; // 更新爷爷对子节点的控制
    pushup(y), pushup(x);
}

破坏平衡的几个形式

LL型

原因：左子树的左子树过长破坏平衡。解决方案：右旋 zig。

RR型

原因：右子树的右子树过长破坏平衡性。解决方案：左旋 zag。

L-R型

原因：左子树的右子树过长导致破坏平衡性。解决方案：左右旋 zag-zig。

细说：先将左子树的右子树，通过左旋，变成左子树的左子树，即 LL 型，然后再右旋，达到平衡。

R-L型

原因：右子树的左子树过长导致破坏平衡性。解决方案：右左旋 zig-zag。

细说：先将右子树的左子树，通过右旋，变成了右子树的右子树，即 RR 型 然后再左旋，达到平衡。

splay操作

我们的 splay 操作就是要将上面几种方式给变成一个平衡的结构，实际上 splay 的代码实现很短。但是实际上这个并不常用，主要用的还是将一个节点转到另一个节点下面，这样可以进行维护区间的操作，具体可以看下下文的代码。

inline void splay(ll x)
{
	for(rl f = fa(x); f = fa(x), f; rotate(x))
		if(fa(f)) rotate(get(f) == get(x) ? f : x);
	root = x;
}

为了保证 splay 的时间复杂度，我们规定每次最后访问到的节点是 x，都要把 x Splay 到根上。

时间复杂度分析

分析什么分析啊，计算机是工科！（just kidding，~~实际上是菜鱼不会分析~~）
这里贴一个复杂度证明想了解的神仙可以自行学习。知道这个复杂度是 \(logn\) 的就行了。

应用

之后就是一些查询插入修改访问之类的了，和二叉搜索树基本上没有多大关联了。

这里一个操作一个操作的展开。

插入

其实本质的思路和二叉搜索树没有多大的区别，主要是最后要 splay 一下维护我们平衡树的结构。

inline void insert(ll key)
{
	ll now = rt,  f = 0;
	while(now) f = now, now = tr[now].s[key>tr[now].key];
	now = newnode(key), fa(now) = f, tr[f].s[key>tr[now].key] = now, splay(now);
}

删除

前面已经说过了二叉搜索树是怎么样实现删除操作的，下面直接放代码了。
u1s1，其实可以直接学成区间的删除，我感觉区间的删除其实好理解一点。。。下面这个看 yxcat 放了我也放一个。QAQ

inline void delete(ll key)
{
	ll now = root, p = 0;
	while(tr[now].key != key && now) p = now, now = tr[now].s[key>tr[now].key]; // 找到要删除的节点
	if(!now) { splay(p); return ; }
	splay(now), ll cur = ls(now);
	if(!cur) { rt = rs(now), fa(rs(now))=0, clear(now); return ; } 
	while(rs(cur)) cur = rs(cur);
	rs(cur) = rs(now), fa(rs(now)) = cur, fa(ls(now)) = 0, clear(now); // 把右儿子接在（左子树的最大权值）下面
	maintain(cur), splay(cur);
}

查询 x 的排名

从根节点开始，根据左子树的 \(size\) 判断我们查询的 \(x\) 在哪棵子树里面；因为一个平衡树里可能有一堆权值是 \(x\) 的点，这里我们本质上是要找到严格小于 \(x\) 的点数 + 1。

每次都往右子树走，左边的子树就给答案贡献了 \(size_ls(now) + 1\) 个比 \(x\) 要小的数。

inline ll rank(ll key)
{
	ll res = 1, now = root, p;
	while(now)
		if(p = now, tr[now].key < key) res += tr[ls(now)].size + 1, now = rs(now);
		else now = ls(now);
	
	return splay(p), res;
}

注意，这里虽然只在树上跑点，没有改变数的结构，但任然要 splay（把splay这个操作当成施法后摇就行了）

查询排名为 k 的数

同理，根据子树 \(size\) 直接判断排名为 \(k\) 的数走哪一边。
这个很多题里面都会用到貌似，建议直接背过

inline void kth(ll rk)
{
	ll now = root;
	while(now)
	{
		ll sz = tr[ls(now)].size + 1;
		if(sz > rk) now = ls(now); // 注意这里没有 = ！！！不然会 T 到恶心，你还得朗读代码才能找出问题来
		else if(sz == rk) break;
		else if(sz < rk) rk -= sz, now = rs(now);
	}
	return splay(now), tr[now].key;
}

查询 x 的前驱

从根节点开始往下走，如果当前点大于等于 x，那么这个的前驱就一定在左子树，我们就往左走；否则，前驱可能在这个点或者在右子树，这个时候我们先用这个节点更新答案，然后再去这个节点的右子树继续找。

inline ll pre(ll key)
{
	ll now = root, ans = 0, p;
	while(now)
		if(p = now, tr[now].key >= key) now = ls(now);
		else ans = tr[now].key, now = rs(now);
	return splay(p), ans;
}

查询 x 的后继

把前驱操作倒过来就好了。

inline ll  suf(ll key)
{
	ll now = root, ans = 0, p;
	while(now)
		if(p = now, tr[now].key <= key) now = rs(now);
		else ans = tr[now].key, now = ls(now);
	return splay(p), ans;
}

一些上面操作的复合版本

这里的 \(splay(a, b)\) 是指的将 a 一路翻转到 b 的下面。

这个更常用一点，因为通过 splay 进行区间操作的话这个会比上面那个好用。

inline void splay(ll x, ll y)
{
	for(rl f=fa(x);f=fa(x), f != y; rotate(x))
		if(fa(f) != y) rotate(get(f) == get(x) ? f : x);
	if(!y) root = x;
}

将一个序列插入到 y 的后面

找到 y 的后继 z。
将 y 旋转到根节点。splay(y, 0);
将 z 转到 y 的下面。 splay(z, y);
将序列加在 z 的左子树下。

思路说明：先将 y 转到根，然后再将 z 转到 y 的下面，这个时候由于原来 z 和 y 是相邻的所以这个时候 z 的左儿子为空，我们将序列建树之后插在这里，就完成了我们插入区间的操作。

删除 \([l, r]\) 这一段

找到 l 的前驱 a，找到 r 的后继 b。
将 a 转到根，将 b 转到根的下面。
此时，b 的左子树就是 \([l, r]\) 就是我们要删除的区间。直接将 b 的左子树清空行了。

思路说明：大致同上，我们找到 a 和 b，之后将 a 转到根，b 转到 a 的下面，我们就可以

find函数

找到下标为 x 的点，原理和二叉搜索树的找排名为 k 的函数相同。注意！我们因为在进行递归操作的时候要一边去找然后一边区 pushdown。同时因为我们会有一个虚点所以最后找到的排名是实际的下标 + 1。

inline ll find(ll x)
{
	ll now = root, x ++ ;
	while(now)
	{
		pushdonw(now); ll sz = tr[ls(now)].size + 1;
		if(sz == x) break;
		else if(sz > x) now = ls(now);
		else now = rs(now), x -= sz;
	}
	return now;
}

reverse

inline void reverse(ll l, ll r)
{
	ll x = find(l - 1); splay(x, 0);
	ll y = find(r + 1); splay(y, x);
	tr[ls(y)].lz ^= 1;
}

build

下面这个是 y总说的沙雕风格的建图，就是直接建成一个链，之后再转成平衡树

inline void build()
{
	root = newnode(0); ll now = root;
	for(rl i=1; i <= n + 1; ++ i, now = rs(now)) tr[now].size = n + 3 - i, rs(now) = newnode(a[i]), fa(rs(now)) = now;
}

下面这个是 y总说的学术风格的建图，直接建成平衡树

inline ll build(ll l, ll r, ll p)
{
    ll mid = l + r >> 1, u = nodes[tt -- ]; // 这个nodes是结合了下面来的,读者自行修改不难(或者要不然干脆就用我这个得了
    tr[u].init(w[mid], p);
    if(l < mid) ls(u) = build(l, mid - 1, u);
    if(mid < r) rs(u) = build(mid + 1, r, u);
    pushup(u); return u;
}

内存回收

对于一部份毒瘤题目，我们并不知道中间的点的个数能有多少，所以为了不爆空间（~~听取MLE声一片，以及惨痛的回忆~~），我们就要进行内存回收。实现起来和理解起来其实都不难

inline void dfs(ll u)
{
	if(ls(u)) dfs(ls(u));
	if(rs(u)) dfs(rs(u));
	nodes[ ++ tt] = u;
}

inline void dele(ll l, ll r)
{
	// balablabala // 这玩意儿具体看题的
	splay(l, 0), splay(r, l);
	dfs(ls(r)); ls(r) = 0; 
	pushup(r), pushup(l); // 从下往上重新维护信息
}

int main()
{
	for(rl i=1; i < N; ++ i) nodes[ ++ tt] = i;
	
	w[0] = w[n + 1] = -INF; // 设个哨兵
	
	for(rl i=1; i <= n; ++ i) cin >> w[i]; // 存储初始值(有的没有就省去这一步)
	
	root = build(0, n + 1, 0);
	
	// balabalabala...
	
	dele(l, r);
}

输出

我们的平衡树一直就是维护的一个中序遍历，所以只需要中序遍历就能够输出出来原序列。

inline void write(ll now)
{
	pushdown(now);
	if(ls(now)) write(ls(now));
	if(tr[now].key) cout << tr[now].key << endl;
	if(rs(now)) write(rs(now));
}

对于序列操作的平衡树实现（完整代码）

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define ll long long 
#define rl register ll 

template <class T>

inline void read(T &res)
{
    char ch = getchar(); bool f = 0; res = 0;
    while(!isdigit(ch)) { f |= ch == '-'; ch = getchar(); } 
    while(isdigit(ch)) { res = (res << 1) + (res << 3) + (ch ^ 48); ch = getchar(); }
    // char ch; bool f = 0;
    // while((ch = getchar()) < '0' || ch > '9') f |= ch == '-';
    // res = ch ^ 48;
    // while((ch = getchar()) <= '9' && ch >= '0') res = (res << 1) + (res << 3) + (ch ^ 48);
    res = f ? ~res + 1 : res;
}

const ll N = 1e5 + 10, INF = 1e15;

struct tree
{
    ll s[2], size, fa, key, lz;
    // tree(){ s[0] = s[1] = size = fa = key = lz = 0; }
}tr[N];

#define ls(x) tr[(x)].s[0]
#define rs(x) tr[(x)].s[1]
#define fa(x) tr[(x)].fa

ll root, idx, a[N];

inline ll newnode(ll key) {tr[++idx].key = key, tr[idx].size = 1; return idx; }
inline void maintain(ll x) {tr[x].size = tr[ls(x)].size + tr[rs(x)].size + 1; }
inline void clear(ll x) {ls(x) = rs(x) = fa(x) = tr[x].size = tr[x].key = 0; }
inline bool get(ll x) {return x == rs(fa(x));} // 我是不是爹的右儿子
inline void rotate(ll x)
{
    ll y = fa(x), z = fa(y); ll c = get(x); // y 是爹， z 是爷， c 是 x 是不是 y 的右儿子 （0 左 1 右）
    if(tr[x].s[c ^ 1]) fa(tr[x].s[c ^ 1]) = y; // 有另一棵子树，就把另一棵子树挂在 x 的父节点上
    tr[y].s[c] = tr[x].s[c ^ 1], tr[x].s[c ^ 1] = y, fa(y) = x, fa(x) = z; // 旋转
    if(z) tr[z].s[y == tr[z].s[1]] = x; // 把我爹原来的位置换成我了
    maintain(y), maintain(x); // 维护子树大小
}

inline void splay(ll x, ll y) // 将 y 视为根，转到 y 的下面 
{
    // cout << "asd" << endl;
    for(rl f = fa(x); f = fa(x),f != y; rotate(x)) // 我是不是转到 y 的下面了
        if(fa(f) != y) rotate(get(f) == get(x) ? f : x);
    if(!y) root = x;
}

inline void pushdown(ll x)
{
    if(!tr[x].lz) return;
    swap(ls(x),rs(x)),tr[ls(x)].lz^=1,tr[rs(x)].lz^=1;
    tr[x].lz=0; return;
}

inline ll find(ll x)
{
    ll now = root; ++ x; // 由于有虚点，我们要找的下标为原来的 + 1
    // cout << now << endl;
    while(now)
    {
        pushdown(now); ll sz = tr[ls(now)].size + 1;
        if(sz == x) break;
        else if(sz > x) now = ls(now);
        else now = rs(now), x -= sz;
    }
    return now;
}

inline void print(ll now)
{
    pushdown(now);
    if(ls(now)) print(ls(now));
    if(tr[now].key) printf("%lld ",tr[now].key);
    if(rs(now)) print(rs(now));
}

inline void reverse(ll l, ll r)
{
    ll x = find(l - 1); splay(x, 0);
    ll y = find(r + 1); splay(y, x);
    tr[ls(y)].lz ^= 1;
}

ll n, m;

inline void build()
{
    root = newnode(0); ll now = root;
    for(rl i=1; i <= n + 1; ++ i, now = rs(now))
        tr[now].size = n + 3 - i, rs(now) = newnode(a[i]), fa(rs(now)) = now;
}

int main()
{
    read(n), read(m);

    for(rl i=1; i <= n; ++ i) a[i] = i;
    
    build();
    
    for(rl i=1; i <= m; ++ i)
    {
        ll l, r; read(l), read(r);
        reverse(l, r);  
    }
    print(root);
    return 0;
}

对于普通平衡树的实现（完整代码）