codeforces#1090 D. New Year and the Permutation Concatenation（打表找规律）

题意：给出一个n，生成n的所有全排列，将他们按顺序前后拼接在一起组成一个新的序列，问有多少个长度为n的连续的子序列和为（n+1）*n/2

题解：由于只有一个输入，第一感觉就是打表找规律，虽然表打出来了，但是依然没有找到规律。。。最后看了别人的题解才发现

  

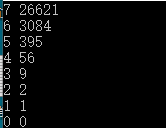
ans [ 3 ] = 1*2*3 + ( ans [ 2 ] - 1 ) * 3

ans[ 4 ] = 1*2*3*4 + ( ans[ 3 ] - 1 ) * 4

感觉每次离成功就差一点点！！！

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=6e5+10;
int num[maxn];
vector<int>ve;
int main()
{
    int k=8;
    while(k--)
    {
        ve.clear();
        cout<<k<<" ";
        for(int i=0; i<maxn; i++)
            num[i]=i;
        do
        {
            for(int i=1; i<=k; i++)
                ve.push_back(num[i]);
        }
        while(next_permutation(num+1,num+k+1));
        int ans=0;
        for(int i=0; i<ve.size(); i++)
        {
            for(int j=i; j<ve.size(); j++)
            {
                if(j-i+1!=k)continue;
                ll cal=0;
                for(int l=i; l<=j; l++)
                    cal+=ve[l];
                if(cal==(k+1)*k/2)
                    ans++;
            }
        }
        cout<<ans<<endl;
    }

    return 0;
}