数学科技
记录一下比较厉害的数学科技。
由于本人数学水平较菜,所以有些地方不太严谨,请各位巨佬指出。
反演
反演实际上就是容斥,在数数题中有广泛运用。
数论分块
数论分块辅助反演可以有很多神秘的效果。
考虑如何在 \(\operatorname{O}(\sqrt n )\) 的时间复杂度内对下列式子进行求值:
不难发现其实 \(\left\lfloor\dfrac{n}{i}\right\rfloor\) 的取值只有 \(\operatorname{O}(\sqrt n)\) 种,所以可以直接暴力跳到每一个不同的取值段的位置,进行计算即可。
code:
for (LL i = 1; i <= n; i = (n / (n / i)) + 1) {
LL r = min(n, (n / (n / i)));
ans += (r - i + 1) * (n / i);
}
莫比乌斯反演
莫比乌斯反演是一个很常用的数论题中的反演。
定义函数 \(\mu(x)\) 满足:
-
\(\mu(x)=1,\ \ (x=1)\)
-
\(\mu(x)=(-1)^n,\ \ (x=p_1p_2\cdots, p_n\ 且\ p_1,p_2,\cdots,p_n\ 为互不相同的质数)\)
-
\(\mu(x)=0,\ \ \operatorname{others}\)
\(\mu(x)\) 有一个非常重要的性质,对于 \(x\in \Z\),\(x=1\) 当且仅当:
证明:
莫比乌斯变换
令 \(F(n)=\sum_{d|n} f(d)\),则 \(f(n)=\sum_{d|n} F(d)\cdot \mu(\frac{n}{d})\)。
证明:
二项式反演
二项式反演的常用形式有两种:
- \(f(i)\) 表示正好 \(i\) 个,\(g(i)\) 表示至多 \(i\) 个。
令:
有:
证明:
- \(f(i)\) 表示正好 \(i\) 个,\(g(i)\) 表示至少 \(i\) 个。
令:
则有:
证明同上。
首先有一个 trick:如果要让距离和最大,那么以重心为根,每个点都只会往重心的另外一个子树中的点匹配。
证明:
- 每个点是否可向外匹配:
根据重心的定义,每个子树大小都是小于等于 \(\frac{n}{2}\) 的,所以除了该子树中的点剩下的点数量是大于等于 \(\frac{n}{2}\),所以一定是可行的。
2.如果不这样进行匹配是否不会更劣
如果有点向同一个子树内的点匹配,可以让每对中的一个点向另外一对中的一个点匹配,这样答案至少会增加 \(4\),所以不这样匹配一定更劣。
那么我们就可以把所有子树的大小拿出来做 dp 了。
直接 dp 显然不好写,考虑容斥。
设 \(f_{i,j}\) 表示前 \(i\) 个子树有 \(j\) 个点向自己子树内匹配,那么有转移方程:
其中 \(a_i\) 是当前子树大小。
那么根据二项式反演,答案就是:
其中 \(c\) 是子树个数。
群
若 \(G\) 为集合,且在 \(G\) 上有二元运算 \(\cdot\),且满足如下性质,则称 \(\left(G,\cdot\right)\) 为一个群:
-
结合律:对于 \(\forall (a,b,c) \in G^3\),有 \(abc=a(bc)\)
-
单位元:有唯一的 \(e\in G\),满足 \(\forall a \in G,ae=ea=a\)
-
逆元:对于 \(\forall a\in G\),存在唯一 \(a^{-1}\in G\),\(a a^{-1}=e\)
满足 1 时,\((G,\cdot)\) 为半群。满足 2,3 时, \((G,\cdot)\) 为幺半群。
一些结论:
结论 1:若 \((a,b,c) \in G^3\),且 \(ab=ac\),有 \(b=c\)
证明:
结论 2:若一个幺半群 \((G,\cdot)\) 满足 \(a\cdot a^{-1}=e\),则 \(G\) 仍为一个群。
证明:
结论 3: 对正整数 \(n\),定义 \(a\in G\) 的 \(n\) 次幂为 \(a^n\),且 \(a^0=e,(a^{-1})^n=a^{-n}\),则有:
1. 对于 \(\forall n,m\), 有 \(a^{n+m}=a^{n}a^{m}\)
2. 对于 \(\forall n,m\), 有 \(a^{nm}=(a^n)^m\)
易证得。
子群与 Largrange 定理
子群的定义
若 \((G,\cdot)\) 为一个群,\((H,\cdot)\) 为一个群且 \(H \subseteq G\),则 \(H\) 为 \(G\) 的子群。记作 \(H\le G\)。
子群判别定理
如果 \(G\) 是一个群,\(H\) 是 \(G\) 的非空子集,那么 \(H\) 是 \(G\) 的子群当且仅当对任意 \((a, b) \in H^2\),都有 \(ab^{-1} \in H\)。
证明:
陪集
对于 \(G\) 的子集 \(H\),若 \(H=xG\),则 \(H\) 为 \(G\) 的左陪集;若 \(H=Gx\),则 \(H\) 为 \(G\) 右陪集。
若 \(H\) 有限,则其左右陪集大小都与其相等。
Lagrange 定理
若 \(H\) 是有限群 \(G\) 的子群,则 \(H\) 的所有不同的左陪集(右陪集)将 \(G\) 划分为了多个大小一样的部
分,从而 \(|H|\) 整除 \(|G|\),分成的部分总数为 \(|G|/|H|\). 定义 \(|G|/|H|\) 为 \(H\) 在 \(G\) 中的指数,记为
\([G : H]\)。
证明:
这里只对于左陪集证明该命题,右陪集的情况类似可证.
由于 \(a = ae \in aH\),故 \(H\) 所有的左陪集可以覆盖 \(G\),只需说明任意两个不同的左陪集都完全不相交
使用反证法, 如果 \(aH \neq bH\) 但是它们有相交的部分,取 \(g \in aH \cap bH\), 则存在 \(h_1\), \(h_2 \in H^2\) 使得 \(g = ah_1 = bh_2\)
注意到 \(aH = \left\{ah|h\in H\right\} = \{b(h_2h_1^{-1}h) | h \in H\}\),而 \(h_2h^{-1}\in H\), 故 \(aH \subseteq bH\),同理可证 \(bH \subseteq aH\),从而 \(aH = bH\), 矛盾.\(\Box\)
群作用
对于群 \(G\) 和集合 \(X\),若有映射 \(\alpha\) 接受 \(G\) 中一个元素和 \(X\) 中的一个元素,返回一个 \(X\) 中的元素,且满足:
-
\(\alpha(e,x)=x\) 对 \(\forall x\in X\) 成立
-
\(\alpha(f,\alpha(g, x))=\alpha(f\circ g,x)\)
则 \(G\) 作用于 \(X\)。
轨道,稳定化子和不动点
取 \(x\in X\),则 \(x\) 的轨道 \(Gx=\{gx|g\in G\}\),\(x\) 的稳定化子为 \(G_x=\{g|gx=x,g\in G\}\)。
取 \(g\in G\),则 \(g\) 的不动点为 \(X^g=\{x\in X|gx=x\}\)。
轨道划分
所有不同轨道将 \(X\) 划分为了多个部分,分成的部分个数记做 \([X:G]\)。
证明与 Lagrange 定理类似。
轨道-稳定子定理
对于 \(\forall x\in X\),\(Gx\) 为 \(G\) 的子群,且 \(|G_x||Gx|=|G|\)。


Burnside 引理
若 \(G\) 作用于 \(X\),则轨道数量是轨道不动点数的平均值。表达式为:
证明:
练习题:


Pólya 定理

(由于本人太菜了,所以直接用官方解释了)
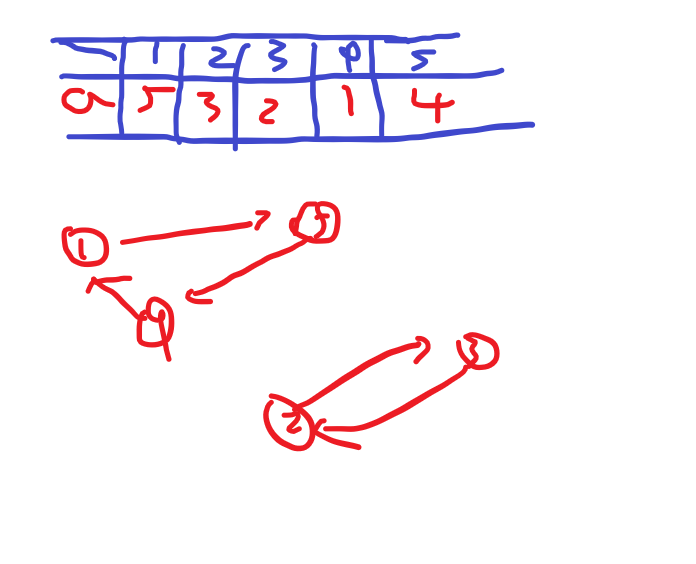
主要就是要注意一下 \(c\)。对于一个置换(或者说排列) \(p\),\(c(p)\) 为该置换所生成图中环的数量,如下图就是一个 \(c(p)=2\) 的排列:
在上述内容中,可以与前文的 Burnside 一起进行理解。 \(C^n\) 是不保证本质不同的染色数,\(G\) 就是可以进行的旋转方式的集合。
由于每个轮换可以进行旋转,所以我们需要对轮换进行染色。不同轮换染色是互不干扰的,所以可以得到 Pólya 定理的公式:
其中 \(m\) 是可以进行染色的颜色个数。
题目
模板题,要求染色方案个数。
假设对一个环旋转 \(k\) 次,那么其置换个数就是 \(\gcd(n,k)\)。
将颜色个数 \(n\) 带入上述的 Pólya 定理的公式中,可以得到答案为:
其中 \(\gcd(i,n)\) 的种类数只有大约 \(n^{\frac{1}{3}}\) 种(每个数的因数个数)。所以说可以用约数容斥去求。总时间复杂度是 \(\operatorname{O}(Tn^{\frac{1}{2}})\)。
FFT
多项式里面最基础的东西(?
想了想还是写一写,都快忘光了。
前置知识:基础高中数学
复数
众所周知对于 \(\forall x\in \R,0\leq x^2\),但为了某些特殊的情况,数学家定义了复数 \(i\) 使得 \(i^2=-1\)。
复数的通常表现形式是 \(a+bi\),其运算规则可以看作一个二项式。
众所又周知,实数有数轴可以表示,那复数有没有图像表示呢?
答案是肯定的,如果我们把复数 \(z=a+bi\) 看作一个点 \((a,b)\),那么我们就可以用平面直角坐标系来表示。这被称为复数域,如图:
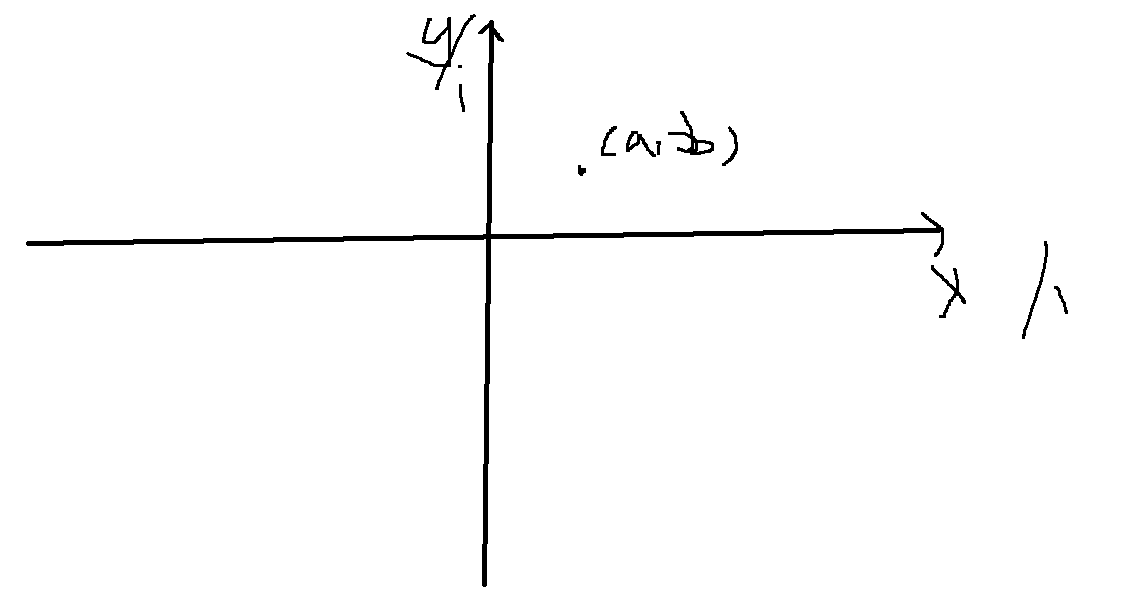
单位圆与 \(n\) 次单位根
单位圆与三角函数密切相关,而 fft 中也要用到单位圆。
单位圆表示的是距离原点的距离为 1 的点的集合。
由于一个点 \((x,y)\) 到原点的距离为 \(x^2+y^2\),所以有 \(x^2+y^2=1\)。发扬惊人的注意力可以发现这个式子长得和三角函数(\(\sin^2 \alpha+\cos^2 \alpha=1\)) 一模一样。事实上,从圆上一个点向坐标轴做垂构建三角形可以得到若该点到 \(x\) 正半轴的弧的角度为 \(\alpha\),则这个点为 \((\cos \alpha,\sin \alpha)\),如图:
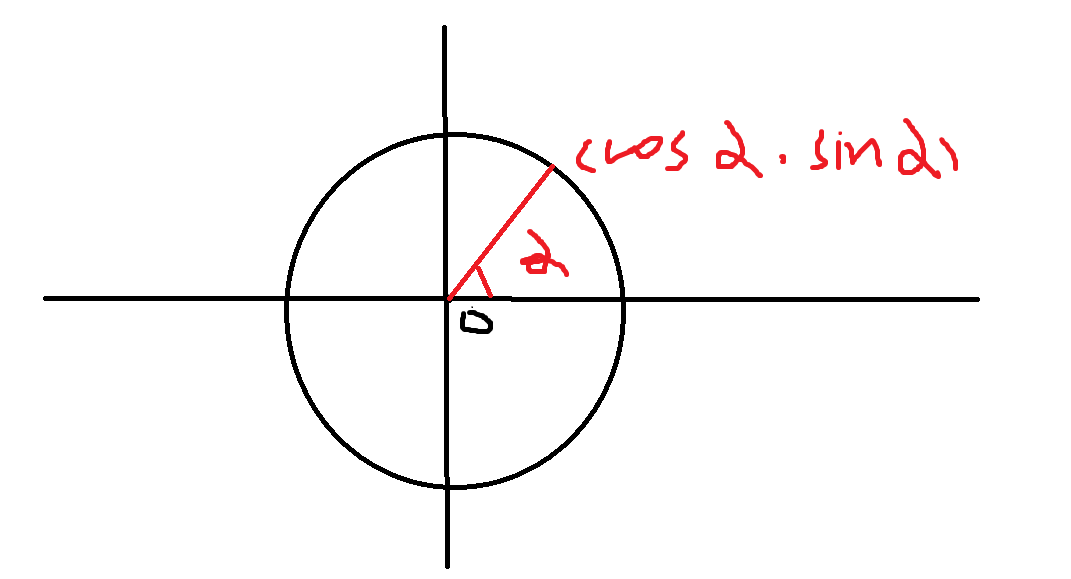
\(n\) 次单位根就是满足 \(x^n=1\) 的 \(x\)。
由于一个 \(n\) 次方程只有 \(n\) 个根,所以得到 在单位圆上,\(n\) 次单位根 \(n\) 等分圆周。
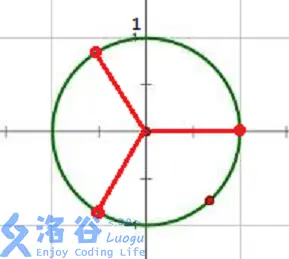
我们用 \(\omega_n\) 来称呼 \(n\) 次单位根,那么每次转 \(\frac{1}{n}\) 圆周就是在原来基础上乘上 \(\omega_n\),比如 \(\frac{2}{n}\) 圆周就是 \(\omega_n^2\)。
为了方便理解,我们可以把 \(\omega_n\) 当作一个实数,其满足所有实数乘法的一些性质(\(\omega_n^x \cdot \omega_n^y=\omega_n^{x+y},(\omega_n^x)^y=\omega_n^{xy}\)),而且还额外满足如下性质:
- \(\omega_{2n}^{2k}=\omega_n^k\)
证明显然。
- 若 \(n\) 为偶数,则 \(\omega_n^{k+\frac{n}{2}}=-\omega_n^k\)
证明:
DFT 的思想
众所周知对于 \(n\) 次函数 \(F(x)\),如果我们已经确定了函数上的 \(n+1\) 个点那么我们就可以通过待定系数法唯一确定这个函数。
对于两个 \(n\) 次多项式 \(f(x)\) 与 \(g(x)\),我们有一个数列 \(X={x_0,x_1,x_2,\cdots\cdots,x_n}\),我们将这个数列带入到 \(f\) 中可以得到 \(n+1\) 个点,其设其为 \((x_0,y_0),(x_1,y_1),\cdots\cdots,(x_n,y_n)\)。同理,将 \(X\) 带到 \(g\) 中可以得到 \((x_0',y_0'),(x_1',y_1'),\cdots\cdots,(x_n',y_n')\),这就是多项式的点值表示法。
令 \(h=f\cdot g\),将 \(X\) 带入 \(h\) 得到 \((x_0'',x_1'',\cdots\cdots,x_n'')\),那么有 \(x_i''=x_i\cdot x_i'\)。这是点值表示法的一个重要性质。
但有一点看上去显然不对,\(h\) 应该有 \(2n+1\) 个点。不过问题不大,再找 \(n\) 个点即可。
所以说点值表示法做乘法的复杂度是 \(\operatorname{O}(n)\) 的。为了转换点值表示与系数表示,我们有了 DFT 与 IDFT。
DFT 就是将点值转化为系数,IDFT 则是 DFT 的逆运算。
考虑下列 \(n\) 次多项式:
我们将其分为两个多项式:
那么我们可以得到:
这一步非常重要。
接下来就可以开始推 FFT 的核心式子了。
核心式子:
- \(F(\omega_n^k)=F_1(\omega_{\frac{n}{2}}^k)+\omega_n^k\cdot F_2(\omega_{\frac{n}{2}}^k)(*)\)
证明:
- \(F(\omega_n^{k+\frac{n}{2}})=F_1(\omega_n^{2k})-\omega_n^{k+\frac{n}{2}}\cdot F_2(\omega_n^{2k})(**)\)
证明:
通过 \((*)\) 式与 \((**)\) 式,我们可以分别求出 \(w_n,w_n^2,\cdots\cdots w_n^{n-1}\) 的点值表示法。
但是问题在于我们并不知道 \(F_1\) 与 \(F_2\)。但我们可以发现 \(F_1\) 和 \(F_2\) 本质是 \(F\) 的子问题,所以我们可以递归求解。
IDFT
有了 DFT,那么就需要有 IDFT 还原。
结论:对点值式做 DFT 时把 \(\omega_n\) 换成 \(\omega_n^{-1}\),最后除以 \(n\) 即可完成。
令点值数列为 \(G\),还原的多项式为 \(F(x)\)。考虑带入 \(\omega_n\) 的过程,有 \(g_k=\sum_{i=0}^{n}(\omega_n^k)^i \cdot f_i(1)\)。
那么结论就可以看作是 \(n\cdot f_k=\sum_{i=0}^{n}(\omega_n^{-k})^i \cdot g_i\)。
证明:
至此就是 DFT(也就是 FFT)的核心思想。
FFT 的实现
前面提到,在做 DFT 时由于划分的 \(F_1\) 和 \(F_2\) 是 \(F\) 的一个子问题,所以我们可以递归求解。但由于 FFT 本身实现需要用到复数,所以其常数很大。所以我们需要更好的实现方式。
考虑得到最终的状态后我们可以用利用倍增实现该算法,所以现在考虑如何找到一个数在操作后的位置。
0 1 2 3 4 5 6 7 第 1 层
0 2 4 6|1 3 5 7 第 2 层
0 4|2 6|1 5|3 7 第 3 层
0|4|2|6|1|5|3|7 第 4 层
(这个东西有个名字叫蝴蝶变换)
观察一下不难发现,这个最终序列中的每个数是原序列的每个数的二进制经过翻转形成的,所以直接预处理即可。
接下来考虑如何计算单位根。
对于一个如下单位圆:
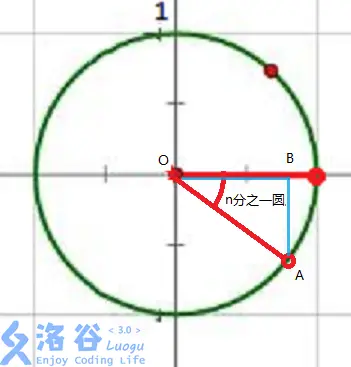
其 \(\frac{1}{n}\) 圆所对的角度就是 \(\frac{2\pi}{n}\),所以其终边的坐标就是 \((\cos \frac{2\pi}{n},\sin \frac{2\pi}{n})\),其单位根就是 \(\cos \frac{2\pi}{n}+i \cdot \sin \frac{2\pi}{n}\)。
有了这些基础之后就可以实现 FFT 了,最后再放一下两个核心式子:
- \(F(\omega_n^k)=F_1(\omega_{\frac{n}{2}}^k)+\omega_n^k\cdot F_2(\omega_{\frac{n}{2}}^k)\)
- \(F(\omega_n^{k+\frac{n}{2}})=F_1(\omega_n^{2k})-\omega_n^{k+\frac{n}{2}}\cdot F_2(\omega_n^{2k})\)
NTT
NTT 相较于 FFT 在 OI 中应用更广,很多数数题都是用 GF 转化后上 NTT。
原根
由于 FFT 需要用到复数,所以其不能解决模意义下的问题,且可能有精度误差,所以我们需要引入原根来解决。
阶:若 \(k\in \Z^+\) 使得 \(a^k\equiv1\pmod{p}\) 且 \(k\) 最小则称 \(k\) 为 \(a\) 在模 \(p\) 意义下的阶,记作 \(\delta_p(a)\)。
原根:满足 \(\delta_p(g)=\phi(p)\) 的 \(g\) 称为 \(p\) 的原根。
用原根替换单位根
考虑在 FFT 中,我们用到了单位根的哪些性质。
- \(\omega_n^k=(\omega_n^1)^k\)
- \(\omega_n^{0~(n-1)}\) 互不相等。
- \(\omega_n^k=\omega_n^{k \mod n}\)
- \(\omega_{2n}^{2k}=\omega_{n}^{k}\)
在模 \(p\) 意义下,对于原根 \(p\),不难通过原根的性质发现 \(\omega_n=g^{\frac{p-1}{n}}\) 是满足前三条性质的,又因为 \((\omega_{2n}^2)=(g^{\frac{p-1}{2n}})^2=g^{\frac{p-1}{n}}=\omega_n\),所以 \(g^{\frac{p-1}{n}}\) 满足需求。
实现的话将 FFT 中的复数改为原根即可,code。
分治 NTT
对于这种自己需要从自己转移过来可以考虑分治。
采用 cdq 分治的思想,每次将当前序列分成两半,用左边的多项式与右边的多项式相乘即可得到该层的贡献。
第二类斯特林数
定义
第二类斯特林数定义为将一个 \(n\) 元集合划分成 \(k\) 个非空集合的方案数,记作 \(\begin{Bmatrix}n \\k\end{Bmatrix}\)。特别的,\(0\le n<k\) 时 \(\begin{Bmatrix}n \\k\end{Bmatrix}=0\),\(\begin{Bmatrix}n \\0\end{Bmatrix}=[n=0]\)
第二类斯特林数有如下递推方式:
考虑该递推式是如何得到的。
- \(\begin{Bmatrix}n-1 \\k-1\end{Bmatrix}\)
该数代表的是将 \(n-1\) 个数划分成 \(k-1\) 个部分的方案数。那么我们将最后一个数另外创建一个集合就得到了一组 \(n\) 个数划分成 \(k\) 个部分的方案。
- \(k\cdot \begin{Bmatrix}n-1 \\k\end{Bmatrix}\)
\(\begin{Bmatrix}n-1 \\k\end{Bmatrix}\) 代表着把 \(n-1\) 个数分成 \(k\) 组,而最后一个数可以放到任意一个集合里,所以说对于前面 \(\begin{Bmatrix}n-1 \\k\end{Bmatrix}\) 中每一种可以拓展出 \(k\) 种。
所以说可以得到上述递推公式。
通项公式
证明:
令 \(F(x)=\sum_{i=0}^{n}\frac{(-1)^i}{i!}\cdot x^i\),\(G(x)=\sum_{i=0}^{n}\frac{i^n}{i!}\cdot x^i\)。那么第二类斯特林数就是 \(F\cdot G\),于是可以用 NTT 在 \(\operatorname{O}(n\log n)\) 的时间复杂度内计算出同一行的第二类斯特林数了。
列生成函数
令 \(b_i=k!\cdot \begin{Bmatrix}n \\k\end{Bmatrix}\),所以只需求出 \(b_n\) 的生成函数即可。
列生成函数如下:
证明:
利用多项式快速幂可以在 \(\operatorname{O}(n\log n\log k)\) 的时间复杂度内求出同一列的第二类斯特林数。
第一类斯特林数
定义
第一类斯特林数定义为将 \(n\) 个数分成 \(k\) 个不同的有向环的方案数,记作 \(\begin{bmatrix}n\\k\end{bmatrix}\)。
相似的,补充 \(0\le n<k\) 时 \(\begin{bmatrix}n\\k\end{bmatrix}=0\),\(\begin{bmatrix}n\\0\end{bmatrix}=[n=0]\)。
第一类斯特林数的递推方式如下:
考虑每一项对方案数的贡献。
- \(\begin{bmatrix}n-1\\k-1\end{bmatrix}\)
该项是指有 \(n-1\) 个数构成 \(k-1\) 个有向环的方案数,对于 \(n\) 可以新开一个环。
- \((n-1)\cdot \begin{bmatrix}n-1\\k\end{bmatrix}\)
该项是通过 \(n-1\) 个数构成 \(k\) 个有向环拓展来的。在每个环种找到一个位置将 \(n\) 插入可得到一种方案。
行生成函数
证明:
列生成函数
证明:
斯特林数的应用
上升/下降幂转次幂
考虑第一类斯特林数的行生成函数:
所以有 \(x^{\overline{n}}=\sum_{i=0}^{n}\begin{bmatrix}n\\i\end{bmatrix}x^i\)。
将 \(-x\) 带入上式,可以得到:
所以有:
次幂转上升/下降幂
考虑组合意义。\(x^n\) 表示将 \(n\) 个球放进 \(x\) 个无编号的盒子的方案数,枚举有几个盒子非空的,有:
与前面一样,跟据上升下降幂之间的关系,有:
斯特林反演
若 \(F(n)=\sum_{k=0}^{n}\begin{Bmatrix} n\\ k\end{Bmatrix}G(k)\),那么有:
证明方式与二项式反演类似,带入即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号