浅谈凸优化
前言:
其实本来暑假就计划写这篇博客的,但因为每天都要上课加上后面的集训天天比赛导致一直拖到了现在。。。
这一类算法比较偏向数学,所以需要一定数学基础。
由于作者的数学不好,这篇文章 可能会 比较好懂一些。
但因为一些众所周知的原因,很多东西的证明可能不是很严谨,所以.....
这一类算法的用处 & 种类很多,并且难度很大(应该属于省选算法),所以可能要更很久。
wqs二分
简介:
wqs 二分是一种可以很好的解决 正好 \(k\) 个限制 的方法。
这个方法通常与 dp 进行结合,优化 dp。
正文:
话说这貌似是这篇博客里唯一一道蓝题
首先有一个很明显的贪心策略。
我们选择边权最小的 \(k\) 条白边,然后对黑边 Kruskal。
但是每次选的边对后面会有影响所以是错误的。
我们把白边数量和代价的关系体现在平面直角坐标系上(\(x\) 表示减少的白边的数量,\(y\) 表示代价的数量):

可以证明,其一定是个下突壳请读者自行证明。
那么我们要选择 \(k\) 个白边就是要找到 \(x=k\) 的那个点的 \(y\) 坐标。
那么其实就相当于有一条直线去切这个下突壳:

考虑怎么找到这个点,我们可以用二分的思想。
不难发现,如果我们给白边的边权减去一个正数,那么白边的个数会递增。
那么就有了单调性,可以直接二分查找那个数,然后跑一遍 Kruskal 计算当前的白边数量。
code:
#include <bits/stdc++.h>
using namespace std;
const int kMaxN = 2e5 + 5;
struct T {
int u, v, w, op;
bool operator<(const T &a) const {
return w == a.w ? op < a.op : w < a.w;
}
} e[kMaxN], a[kMaxN];
int n, m, k, fa[kMaxN];
int find(int x) {
return fa[x] == x ? x : fa[x] = find(fa[x]);
}
int C(int x) {
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
for (int i = 1; i <= m; i++) {
a[i] = e[i];
a[i].w -= !a[i].op * x;
}
sort(a + 1, a + m + 1);
int cnt = 0;
for (int i = 1; i <= m; i++) {
if (find(a[i].u) != find(a[i].v)) {
cnt += !a[i].op;
fa[find(a[i].u)] = find(a[i].v);
}
}
return cnt;
}
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= m; i++) {
cin >> e[i].u >> e[i].v >> e[i].w >> e[i].op;
e[i].u++, e[i].v++;
}
int l = -100, r = 100;
for (int mid; l < r;) {
mid = l + r >> 1;
int x = C(mid);
if (x >= k) {
r = mid;
} else {
l = mid + 1;
}
}
for (int i = 1; i <= m; i++) {
e[i].w -= !e[i].op * r;
}
sort(e + 1, e + m + 1);
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
int ans = 0;
for (int i = 1; i <= m; i++) {
if (find(e[i].u) != find(e[i].v)) {
fa[find(e[i].u)] = find(e[i].v);
ans += e[i].w;
}
}
cout << ans + r * k;
return 0;
}
PS:排序时以边权做第一关键字,白边靠前为第二关键字。
最后加上代价的时候代价要算 \(k\) 遍,而不是方案中白边的数量(这表现了可以用黑边替换一些白边使得其正好为 \(k\) )。
再来看一道类似的题。
我们考虑把所有与 \(s\) 相连的边染成白色的边,其余边染成黑色的边。
剩下的就和前面一道题一样了。
code:
#include <algorithm>
#include <iostream>
using namespace std;
using LL = long long;
const int kMaxN = 5e5 + 5;
LL fa[kMaxN], n, m, s, k, ans, cnt;
struct E {
LL u, v, w;
bool operator<(const E &a) const {
return w == a.w ? (u == k || v == k) > (a.u == k || a.v == k) : w < a.w;
}
} a[kMaxN];
int find(int x) {
return x == fa[x] ? x : fa[x] = find(fa[x]);
}
int C(int x) {
ans = cnt = 0;
for (int i = 1; i <= m; i++) {
a[i].w += (a[i].u == s || a[i].v == s) * x;
}
sort(a + 1, a + m + 1);
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
for (int i = 1; i <= m; i++) {
if (find(a[i].u) != find(a[i].v)) {
fa[find(a[i].u)] = find(a[i].v);
cnt += a[i].v == s || a[i].u == s;
ans += a[i].w;
}
}
for (int i = 1; i <= m; i++) {
a[i].w -= (a[i].u == s || a[i].v == s) * x;
}
return cnt;
}
int main() {
cin >> n >> m >> s >> k;
for (int i = 1; i <= m; i++) {
cin >> a[i].u >> a[i].v >> a[i].w;
}
LL l = -3e4, r = 3e4;
if (C(r) > k) {
cout << "Impossible";
} else if (C(l) < k) {
cout << "Impossible";
} else {
for (int mid; l < r; C(mid) <= k ? r = mid : l = mid + 1) {
mid = l + r >> 1;
}
C(r);
cout << ans - r * k;
}
return 0;
}
斜率优化:
前言:
斜率优化也是用来优化 dp 的。
这一类 dp 的转移方程一般为
注意:\(a_i,b_j,c_i\) 可以是一个式子,\(c_i\) 可以没有,式子的重点在于 \(a_i \times b_j\)。
正文:
一般斜率优化
看到这题,不难想到方程:
为了方便描述,下文我们设 \(s_i=\sum_{j=1}^{j\le i}c_j,a_i=s_i+i,b_i=a_i+L+1\)
那么转移方程就变为了
这样就获得了一个 \(\operatorname{O}(n^2)\) 的算法。
然后就有人想问了,既然状态只有 \(n\) 个,那么能不能把时间复杂度优化到 \(\operatorname{O}(n)\) 呢?
于是就有了斜率优化。
我们把转移式展开,并去掉 \(\min\) 方便观察。
那么考虑两个可以转移的点(这里设为 \(x\) 和 \(y\)),如果 \(x\) 优于 \(y\) 会有什么性质。
我们将 \(i\) 看成常量。
设 \(t_i=f_i+(b_i)^2\),得原式为:
注意:因为不等式的性质,所以要保证 \(b_y\le b_x\)。
令 \(Y(j)=t_j,X(j)=b_j,K(i)=2a_i\) (注意,这里把 \(i\) 看成常量)。
那么得到
然后就可以发现这个式子和斜率式很像。
那么把每个 \(j\) 都放入平面直角坐标系中(为了方便讨论就只放三个)。
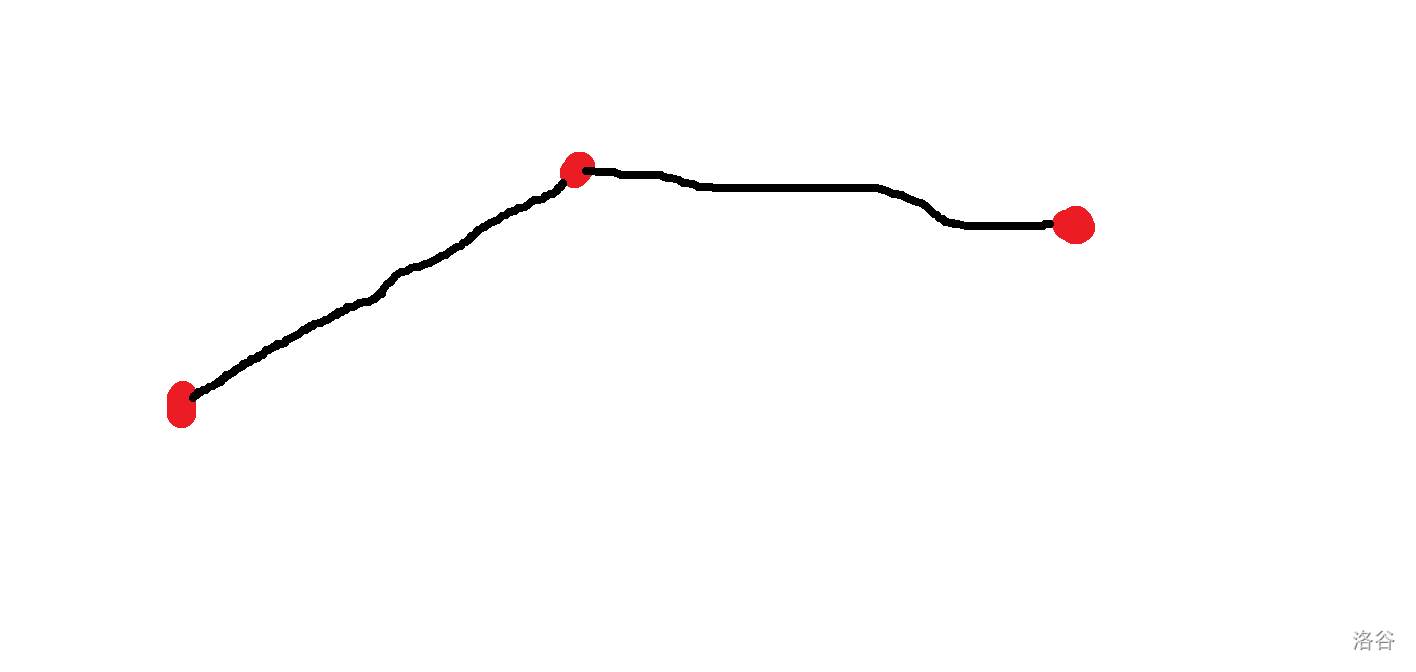
然后就分类讨论斜率关系,就可以得到中间那个点永远不会是最优的点因为作者太懒了就不解释了(相信大家的数学水平都比作者好)。
那么我们就得到了一个下突壳:

你没看错,这就是讲 wqs 二分的那张图。
然后我们要把斜率小于等于 \(K(i)\) 的全部删除,这样就得到了 \(i\) 的最转移点。
这个过程可以用单调队列实现。
来整理一下过程:
-
把所有点入队,入队时判断是否是下突壳,不是就把当前的倒数第二个点删去,直到是一个下突壳。
-
如果对首的斜率比 \(K(i)\) 小,将队首出队。
但是这样求出一个点的最优转移点是 \(\operatorname{O}(n)\) 的,要求 \(n\) 个点又变成 \(n^2\) 了。
你没听错,通过如此复杂度推到最后得出了一个和暴力时间复杂度相同且常数更大的算法。
考虑还有什么性质可以优化。
由于这道题中的 \(K(i)=2\times (s_i+i)\),所以 \(K(i)\) 是单调不减的。
那么如果无法满足前面的 \(K(i)\) 的条件,后面的 \(K(i)\) 也一定无法满足,所以不需要对于每个点把前面的点重新入队。
code:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int kMaxN = 2e5 + 5;
LL n, L, l, r, a[kMaxN], b[kMaxN], s[kMaxN], f[kMaxN], q[kMaxN];
LL X(int x) {
return 2LL * b[x];
}
LL Y(int x) {
return f[x] + b[x] * b[x];
}
double slope(int x, int y) {
return 1.0 * (Y(x) - Y(y)) / (X(x) - X(y));
}
int main() {
cin >> n >> L;
for (int i = 1; i <= n; i++) {
cin >> a[i];
s[i] = s[i - 1] + a[i];
a[i] = s[i] + i, b[i] = a[i] + L + 1;
}
l = r = 1;
b[0] = L + 1;
for (int i = 1; i <= n; i++) {
for (; l < r && slope(q[l + 1], q[l]) < a[i] * 1.0; l++) {
}
int j = q[l];
f[i] = f[j] + (a[i] - b[j]) * (a[i] - b[j]);
for (; l < r && slope(i, q[r]) < slope(q[r], q[r - 1]); r--) {
}
q[++r] = i;
}
cout << f[n];
return 0;
}
这里再讲一个推斜率优化式子的小技巧(如果用我上述的那种方法有点麻烦)。
我们可以把式子变成 \(y=kx+b\) 的形式。
其中 \(y,x\) 只含有 \(j\) 的项,\(k,b\) 是有 \(i\) 的项,然后把式子一一对应即可。
斜率非递增优化
用单调栈代替单调队列,也就是队首不出队。
然后二分一个最大 / 最小的满足斜率要求的位置进行转移即可。
wqs 二分套斜率优化
考虑正常 dp。
设 \(f_{i,j}\) 表示还剩 \(i\) 个人,分成了 \(j\) 段的最大价值。
那么转移方程如下:
然而这样时间复杂度是 \(\operatorname{O}(n^2k)\) 的,无法通过。
我们考虑如果没有 \(k\) 个限制怎么做。
设 \(f_i\) 表示还剩 \(i\) 个人时的最大价值,转移方程同上:
转化为 \(y=kx+b\) 的形式:
然后这个式子就可以用斜率优化优化到 \(O(n)\) 了。
那么考虑加入 \(k\) 的限制。
注意到段数越多其价值也一定越多,且其形成了一个下突壳(具体可以跑一遍第一类 dp),而 wqs 二分可以完成正好 \(k\) 个这一类的问题。
所以可以二分出每选择一段所要增加的代价,段数越多代价也越高。
那么怎么求出段数呢?可以用递推的思想。
在斜率优化的过程中进行双关键字 dp。
设 \(g_i\) 表示还剩 \(i\) 个人按照当前最优方案分成了几段。
那么 \(g_i=g_j+1\),\(j\) 是转移 \(f_i\) 时的最优转移点。
时间复杂度:\(\operatorname{O}(n\log V)\)
code:
#include <iostream>
using namespace std;
#define double long double
const int kMaxN = 1e5 + 5;
const double eps = 1e-12;
int n, k, l, r, q[kMaxN], g[kMaxN];
double f[kMaxN];
double X(int x) {
return x;
}
double Y(int x) {
return f[x];
}
double slope(int x, int y) {
return (Y(x) - Y(y)) / (X(x) - X(y) == 0 ? 1e9 : X(x) - X(y));
}
int C(double x) {
fill(f, f + n + 1, 0);
fill(g, g + n + 1, 0);
l = r = 1;
for (int i = 1; i <= n; i++) {
for (; l < r && slope(q[l], q[l + 1]) >= 1.0 / (i * 1.0); l++) {
}
int j = q[l];
f[i] = f[j] + (i - j) * 1.0 / (i * 1.0) + x, g[i] = g[j] + 1;
for (; l < r && slope(q[r - 1], q[r]) <= slope(q[r], i); r--) {
}
q[++r] = i;
}
return g[n];
}
int main() {
cin >> n >> k;
double l = -1e6, r = 1e6;
while (r - l > eps) {
double mid = (l + r) / 2;
int v = C(mid);
if (v <= k) {
l = mid;
} else {
r = mid;
}
}
C(l);
printf("%.9Lf", f[n] - l * k);
return 0;
}
一般凸优化
还不会,咕咕咕......


 浙公网安备 33010602011771号
浙公网安备 33010602011771号