线段树

线段树不是完全二叉树
线段树式平衡二叉树
堆也是平衡二叉树

如果区间有n的元素 数组需要多少多少节点?
如果 $n = 2^k$ 只需要2n的空间
最坏的情况,如果$n = 2^k + 1$

需要4n的空间

public class SegmentTree<E> {
    private E[] data;
    private E[] tree;
    private Merger<E> merger;
    public SegmentTree(E[] arr,Merger<E> merger) {
        this.merger = merger;
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
        buildSegmentTree(0,0,data.length -1);
    }

    private void buildSegmentTree(int treeIndex, int l, int r) {
        if(l == r){
            tree[treeIndex] = data[l];
            return;
        }
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = l + (r-l) / 2;
        buildSegmentTree(leftTreeIndex,l,mid);
        buildSegmentTree(rightTreeIndex,mid+1,r);
        tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
    }

    public int getSize(){
            return data.length;
        }
        public E get(int index){
        if(index < 0 || index >data.length)
            throw  new IllegalArgumentException("Index is illegal.");
        return data[index];
        }
     private int leftChild(int index){
        return index * 2 + 1;
     }
     private int rightChild(int index){
         return index * 2 + 2;
     }
     public Object query(int queryL, int queryR){
        //判断要查询的索引不能小于0 不能越界 左边的索引小于右边的。
        if(queryL<0 || queryL >= data.length
        || queryR <0 || queryR >= data.length || queryL > queryR)
            throw new IllegalArgumentException("Index is illegal.");
        //调用递归函数
        return query(0,0,data.length -1,queryL,queryR);
     }

    private E query(int treeindex, int l, int r, int queryL, int queryR) {
        //终止条件
        if(l == queryL && r == queryR){
            return tree[treeindex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex =leftChild(treeindex);
        int rightTreeIndex = rightChild(treeindex);
        if(queryL >= mid +1 )
            return query(rightTreeIndex,mid+1,r,queryL,queryR);
        else if(queryR <= mid)
            return query(leftTreeIndex,l,mid,queryL,queryR);
        //如果左边有一部分 右边有一部分  左边查出来 右边查出来 合在一起。
        E leftResult = query(leftTreeIndex,l,mid,queryL,mid);
        E rightResult = query(rightTreeIndex,mid+1,r,mid +1,queryR);
        return merger.merge(leftResult,rightResult);


    }

    @Override
     public String toString(){
        StringBuilder res = new StringBuilder();
        res.append('[');
        for(int i =0;i<tree.length;i++){
            if(tree[i] != null)
                res.append(tree[i]);
            else
                res.append("null");
            if(i != tree.length )
                res.append(",");
        }
        res.append("]");
        return res.toString();

     }



}

public interface Merger<E> {
    E merge(E a,E b);
}

main.java

public class Main {
    public static void main(String[] args) {
        Integer[] nums = {-2,0,3,-5,2,-1};
        SegmentTree<Integer> segmentTree =new SegmentTree<>(nums,(a,b) -> a +b);
        System.out.println(segmentTree.query(0,2));


    }
}

核心代码

 private void buildSegmentTree(int treeIndex, int l, int r) {
        if(l == r){
            tree[treeIndex] = data[l];
            return;
        }
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = l + (r-l) / 2;
        buildSegmentTree(leftTreeIndex,l,mid);
        buildSegmentTree(rightTreeIndex,mid+1,r);
        tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
    }

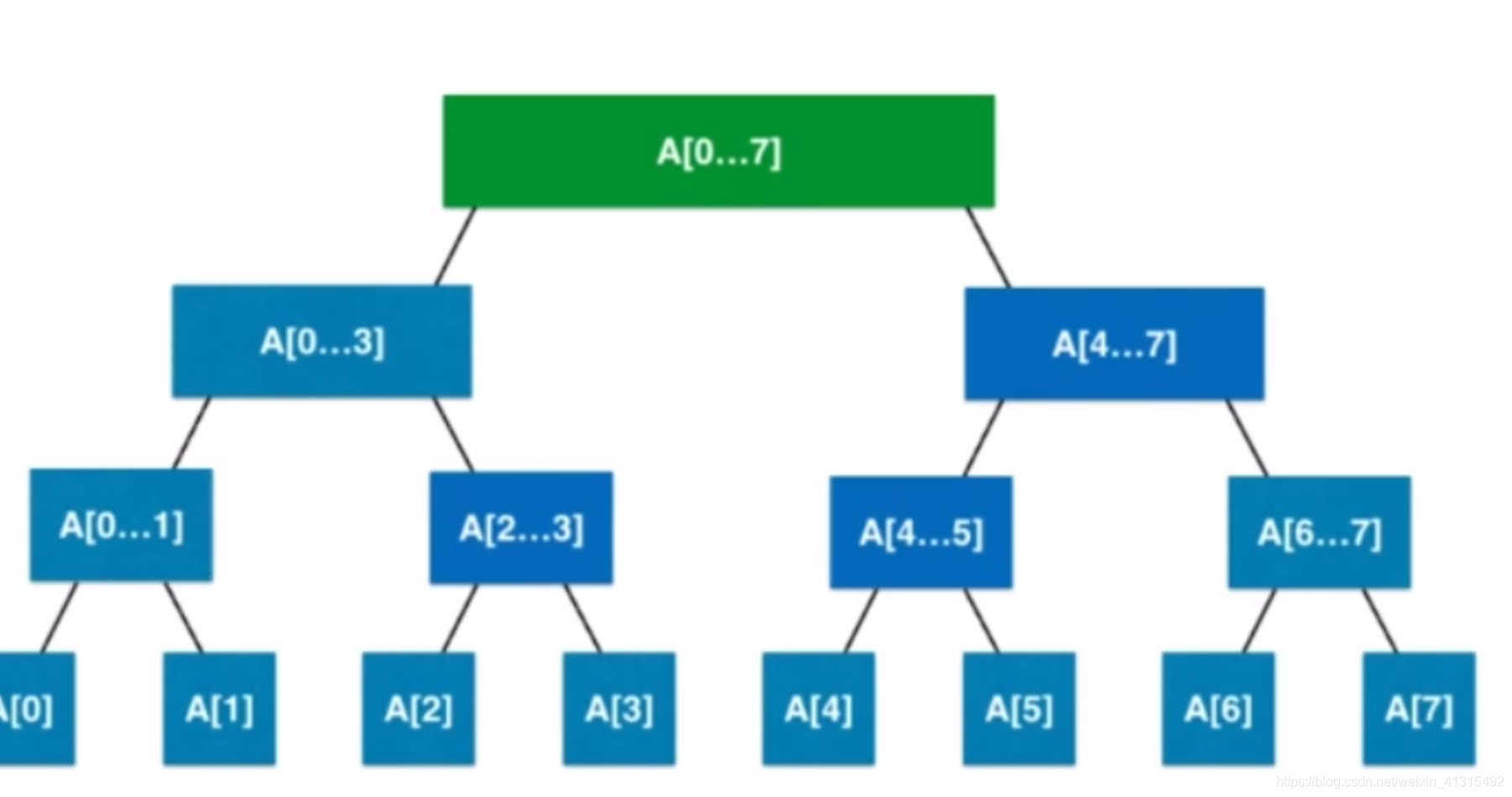
线段树 给我的感觉像是 一个组织 然后每个组织都有头目 管理着他底下有几个人 平均年龄 身高 通过这样层层分级 这样 如果需要统计 就不需要单独 个体循环遍历 去加起来 而是先去找能不能找到完全符合的划分 找不到 再去找包含这些数的几个划分 相加。
使用递归
递归退出条件 当左边和右边的索引都一致 此时只有一个元素 一个单独的元素 则不需要再划分了

	 int leftTreeIndex = leftChild(treeIndex);
     int rightTreeIndex = rightChild(treeIndex);	

 private int leftChild(int index){
        return index * 2 + 1;
     }
     private int rightChild(int index){
         return index * 2 + 2;
     }

线段树的查找操作

    private void set(int treeIndex, int l, int r, int index, E e) {
        if(l == r)
        {
        //如果左边和右边相等 就 更新这个e
            tree[treeIndex] = e ;
            return;
        }
        //计算数范围 比如 10个数 第二次递归 mid 就是 4 
        int mid  = l + (r - l) / 2;
        //找到左孩子节点
        int leftTreeIndex =leftChild(treeIndex);
        //找到右孩子节点
        int rightTreeIndex = rightChild(treeIndex);
        //如果索引 mid 小于索引说明 要更新的节点在右边 反之在左边
        if(index >= mid +1)
            set(rightTreeIndex,mid+1,r,index,e);
        else
            set(leftTreeIndex,l,mid,index,e);
        tree[treeIndex] = 
        //最后合并左右 2个节点
       merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
    }

懒惰更新

对一个区间进行更新

对区间进行更新 会造成所有的叶子节点都要更新 复杂度O(N) 所以可以使用 lazy数组记录 未更新内容 懒惰更新 复杂度Olog(N)

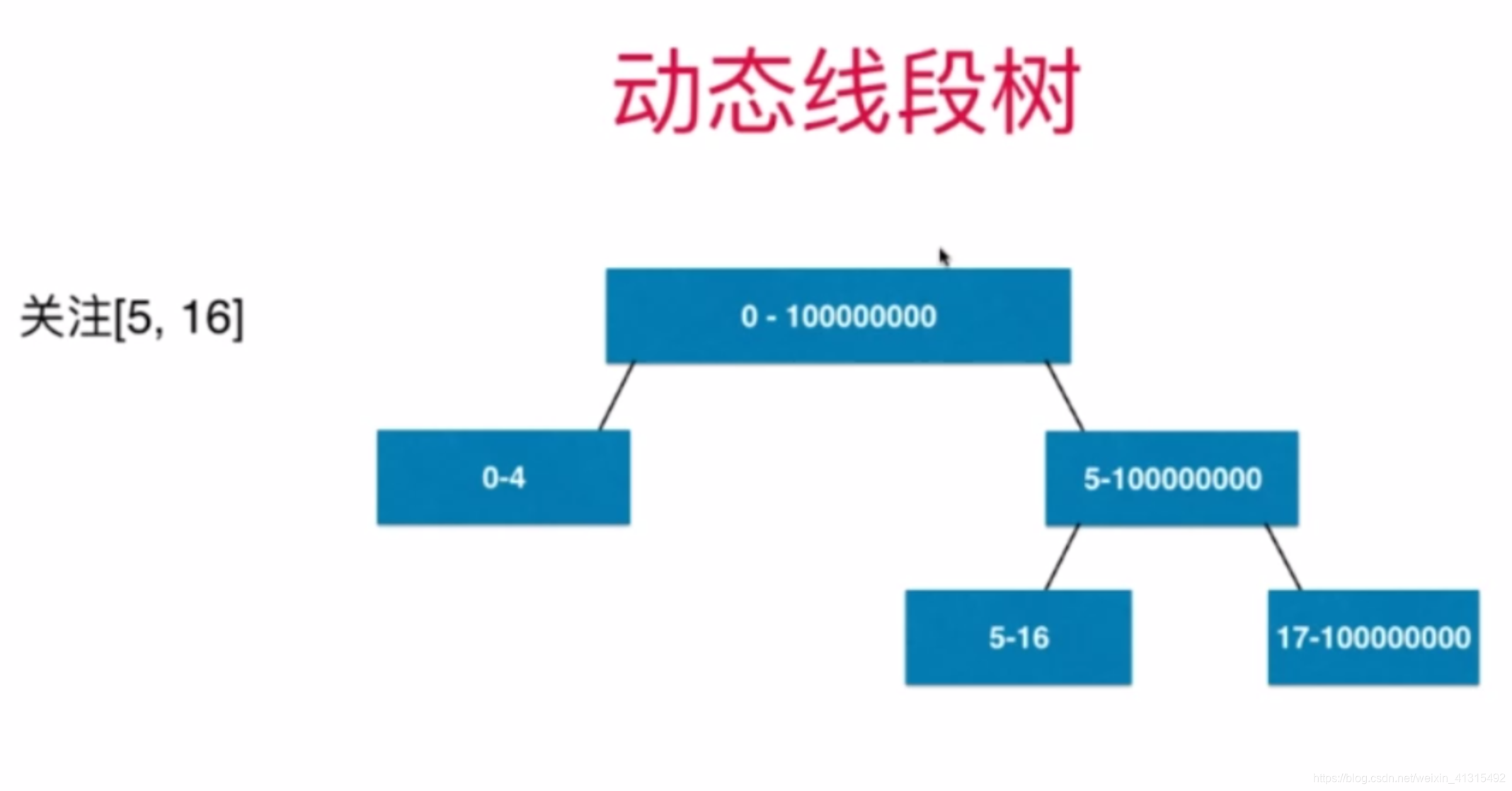
动态线段树