机器学习(二)-一元线性回归算法(代码实现及数学证明)

解决回归问题
思想简单,实现容易
许多强大的非线性模型的基础
结果具有很好的可解释性
蕴含机器学习中的很多重要思想

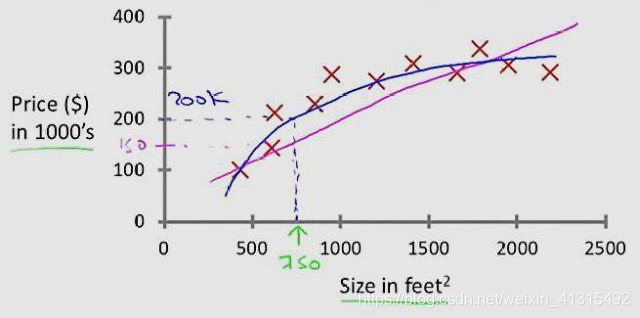
回归问题:连续值

如果样本特征只有一个称为简单线性回归 y=ax + b

通过训练数据集预测出来的值我们希望它和真实值之间差距尽可能的小
$y^{(i)} - \hat{y}$
如果想要计算距离我们自然会想到可以使用绝对值
$|y^{(i)} - \hat{y}^{(i)}|$
绝对值在计算中不是特别好的方式方程不可导没法求最优解
$(y^{(i)} - \hat{y}^{(i)})^2$
另外计算距离还可以想到的是使用平方计算并且他是一个凸函数连续且处处可导在后续计算中会比较方便求极值。(凸优化中的最小二乘法)
考虑所有样本:
： $(i)$ 特征个数
: $(m)$ 为样本点个数
${argmin}\sum_{i=1}^{m}(y^{(i)} - \hat{y}^{(i)})^2$
由于 $\hat{y}^{(i)} = ax^{(i)} + b$
带入得 ${argmin}\sum_{i=1}^{m}(y^{(i)} - ax^{(i)} - b)^2$
目标找到 a 和 b 使方程 $\sum_{i=1}^{m}(y^{(i)} - ax^{(i)} - b)^2$ 尽可能的小.

$\sum_{i=1}^{m}(y^{(i)} - ax^{(i)} - b)^2$ 一般称为损失函数(loss function).也可以成为效用函数(utility function)

由线性回归可以了解到机器学习算法的解决问题的一般思路:
通过分析问题,确定问题的损失偶函数或效用函数。
通过优化损失函数或者效用函数,获得机器学习的模型。
包括但不限于以下算法都是使用这种思路:

线性回归
SVM
多项式回归
神经网络
逻辑回归
…

最小二乘法求导简单证明:

$\sum_{i=1}^{m}(y^{(i)} - ax^{(i)} - b)^2$

对a求导: $\frac{\partial{J(a,b)}}{\partial{a}} = 0$

对b求导: $\frac{\partial{J(a,b)}}{\partial{b}} = 0$

$\frac{\partial{J(a,b)}}{\partial{b}} = 0$ = $\sum_{i=1}^m2(y^{(i)}-ax^{(i)}-b)(-1)$

$\sum_{i=1}^m2(y^{(i)}-ax^{(i)}-b)(-1)$ = 0

等式左右2便除以 -2得:

$\sum_{i=1}^my^{(i)}-a\sum_{i=1}^mx^{(i)}-\sum_{i=1}^mb$ = 0

由于b是常数 mb = $\sum_{i=1}^mb$

$\sum_{i=1}^my^{(i)}-a\sum_{i=1}^mx^{(i)}-mb$ = 0

$mb$ = $\sum_{i=1}^my^{(i)} - a\sum_{i=1}^mx^{(i)}$

由于 $\sum_{i=1}^my^{(i)}=m\bar{y}$

$a\frac{\sum_{i=1}^mx^{(i)}}{m}=a\bar{x}$ m个x的和除以m得到的是x的均值

可得:

$b =\bar{y}-a\bar{x}$

J所以对b求导得: $b =\bar{y}-a\bar{x}$

再求 J对a求导:
$\frac{\partial{J(a,b)}}{\partial{a}} = 0$ = $\sum_{i=1}^m2(y^{(i)}-ax^{(i)}-b)(-x^{(i)})$
提出-2得:
$\sum_{i=1}^m(y^{(i)}-ax^{(i)}-b)x^{(i)}=0$
把上面求出来的 $b =\bar{y}-a\bar{x}$ 带入得:
$\sum_{i=1}^m(y^{(i)}-ax^{(i)}-\bar{y}+a\bar{x})x^{(i)}=0$
$\sum_{i=1}^m(x^{(i)}y^{(i)}-ax^{(i)}x^{(i)}-\bar{y}x^{(i)}+a\bar{x}x^{(i)})=0$
$\sum_{i=1}^m(x^{(i)}y^{(i)}-\bar{y}x^{(i)}-ax^{(i)}x^{(i)}+a\bar{x}x^{(i)})=0$
$\sum_{i=1}^m(x^{(i)}y{(i)}-x^{(i)}\bar{y}) - \sum_{i=1}^m(a(x^{(i)})^2 - a\bar{x}x^{(i)})$
化简可得:
$\sum_{i=1}^m(x^{(i)}y{(i)}-x^{(i)}\bar{y}) - a\sum_{i=1}^m((x^{(i)})^2 - \bar{x}x^{(i)})=0$
$a = \frac{\sum_{i=1}^m(x^{(i)}y{(i)}-x^{(i)}\bar{y})}{\sum_{i=1}^m((x^{(i)})^2 - \bar{x}x^{(i)})}$
变换公式:
$\sum_{i=1}^mx^{(i)}\bar{y}=\bar{y}\sum_{i=1}^{m}x^{(i)}=m\bar{y}\bar{x}=\bar{x}\sum_{i=1}^{m}y^{(i)} =\sum_{i=1}^{m} \bar{x}y^{(i)}$
$m\bar{y}\bar{x}=\sum_{i=1}^{m}\bar{y}\bar{x}$
公式a 可变为(变换后的公式能用矩阵表示在计算机中是非常方便的):
$a =\frac{\sum_{i=1}^{m}(x^{(i)}y^{(i)}-x^{(i)}\bar{y}-\bar{x}y^{(i)}+\bar{x}\cdot \bar{y})}{\sum_{i=1}^{m}((x^{(i)})-\bar xx^{(i)}-\bar xx^{i}-\bar {x}^{2} )}$ = $\frac{\sum_{i=1}^{m}(x^{(i)}-\bar{x})(y^{(i)}-\bar{y})}{\sum_{i=1}^{m}(x^{(i)}-\bar{x})^2}$

最后可得:
$b =\bar{y}-a\bar{x}$
$a =\frac{\sum_{i=1}^{m}(x^{(i)}-\bar{x})(y^{(i)}-\bar{y})}{\sum_{i=1}^{m}(x^{(i)}-\bar{x})^2}$

变换成矩阵表示:
$x =(x_1,x_2,x_3,.....,x_m)^T$
$x_d =(x_1 - \bar x,x_2- \bar x,x_3- \bar x,.....,x_m- \bar x)^T$
$y =(y_1,y_2,y_3,.....,y_m)^T$
$y_d =(y_1 - \bar y,y_2 - \bar y,y_3 - \bar y,.....,y_m - \bar y)^T$

$a = \frac {x_d^Ty_d}{x_d^Tx_d}$ b= $y_d-ax_d$

代码实现:

导入需要的模块
import numpy as np
import matplotlib
import matplotlib.pyplot as plt

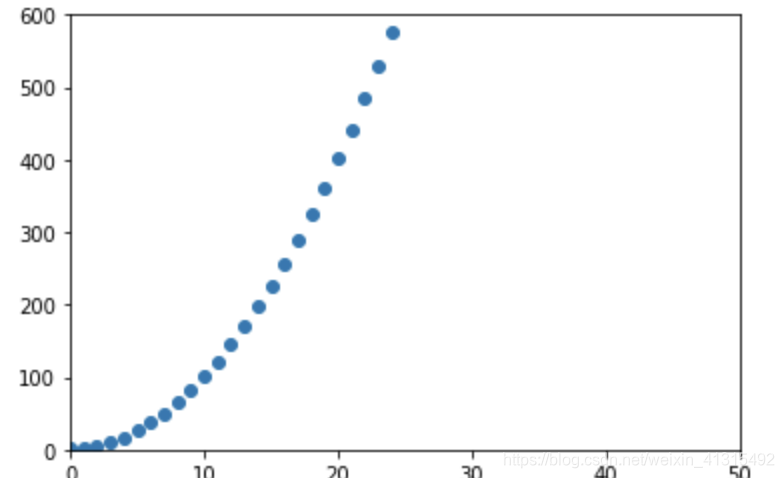
#随机创建 25个点
x = np.arange(25)
#将x映射成x^2 +1 上的点y
y =  x ** 2 + 1

画出图形

plt.scatter(x,y)
plt.axis([0,50,0,600])
plt.show()

#求x,y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

非向量化计算a,b需要循环m个样本遍历效率较低

num = 0.0
d = 0.0
for x_i, y_i in zip(x,y):
	#遍历计算a 公式的分子部分
    num +=(x_i - x_mean) *(y_i -y_mean)
    #计算a 分母部分
    d += (x_i - x_mean) ** 2
#根据公式计算出a 和 b
a = num / d
b = y_mean - a * x_mean

使用循环 1.1m 和使用矩阵 20ms 性能差距 50倍

向量计算方式

num = (x_train - x_mean).dot(y_train - y_mean)
d = (x_train - x_mean).dot (x_train - x_mean)

计算出来a和b 来看看训练效果

y_predict = a * x + b
plt.scatter(x,y)
plt.plot(x,y_predict,color ='r')

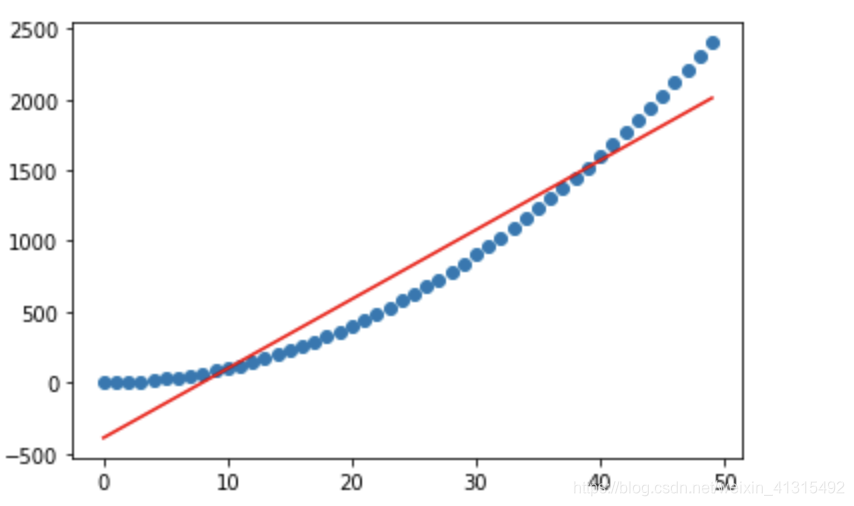
一元线性回归是一条直线对于高次方程效果较差。图中对二次方程的拟合

封装算法

import numpy as np
class SimpleLinearRegression:
    def __init__(self):
        """初始化 Simple Linear Regression 模型"""
        self.a_ =None
        self.b_ =None
    def fit(self,x_train,y_train):
        """根据数据及x_train,y_train 训练Simple Linear Regression 模型"""
        assert x_train.ndim == 1,\
        "Simple Linear Regressor can only only solve single feature traing data."
        assert len(x_train) == len(y_train),\
        "the size of x_train must be equal to the size of y_train"
        x_mean = np.mean(x_train)
        y_mean = np.mean(y_train)
        num = (x_train - x_mean).dot(y_train - y_mean)
        d = (x_train - x_mean).dot (x_train - x_mean)
        self.a_ = num / d
        self.b_ = y_mean - self.a_ * x_mean
        return self
    def predict(self,x_predict):
        """给定带预测数据集x_predict"""
        assert x_predict.ndim == 1, \
            "Simple Linear Regressor can only only solve single feature traing data."
        assert self.b_ is not None and self.a_ is not None, \
            "must fit before predict!"
        return [self._predict(x) for x in x_predict ]
    def _predict(self,x):
        return self.a_ * x + self.b_
    def __repr__(self):
        return "SimpleLinearRegression()"

评测标准

训练完要怎么评价训练模型的好坏?
分类的准确度:accuracy
按照训练损失函数的公式 $\sum_{i=1}^m(y^{(i)}_{test} - \hat {y}^{(i)}_{tets})^2$ 去计算预测的值和真实值之间距离平方这样可行吗?
想一下这样一个场景如果有2个人都训练自己的模型但是人家误差只有几十你却有几百难道他的模型就一定比你好吗?
和m有关? 想象以下你的测试集有100 个而他的测试集只有10 差距能不大吗。那怎么解决呢？平均下?

MSE: $\frac {1}{m}\sum_{i=1}^m(y^{(i)}_{test} - \hat {y}^{(i)}_{tets})^2$ 均方误差MSE(Mean Squared Error)
RMSE: $\sqrt{\frac {1}{m}\sum_{i=1}^m(y^{(i)}_{test} - \hat {y}^{(i)}_{tets})^2}$ 均方根误差RMSE(Root Mean Squared Error) 由于计算差距平方了相当于单位平方了比如你要预测的是价格(万元)但是计算的误差是万元方所以在观测的时候数据可能不直观。
$\frac {1}{m}\sum_{i=1}^m|y^{(i)}_{test} - \hat {y}^{(i)}_{tets}|$ 平均绝对误差MAE(Mean Absolute Error)

实现代码

def root_mean_squared_error(y_true,y_predict):
    assert len(y_true) == len(y_predict),\
    "the size of y_true must be equal to the size of y_predict"
    return np.sqrt(np.sum((y_predict - y_true) ** 2) / len(y_true))
def mean_squared_error(y_true,y_predict):
    """MSE"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"
    return np.sum((y_predict - y_true) ** 2) / len(y_true)
def mean_absolute_error(y_true,y_predict):
    """MAE"""
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"
    return  np.sum(np.absolute((y_predict - y_true))) / len(y_true)

测试代码

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from ml_utils.data_split import train_test_split
from sklearn import datasets
from LinearRegression.SimpleLinearRegression import SimpleLinearRegression
from ml_utils.metrics import mean_absolute_error,mean_squared_error,root_mean_squared_error
if __name__ == '__main__':
    boston = datasets.load_boston()
    x = boston.data[:, 5]
    y = boston.target
    x = x[y < 50.0]
    y = y[y < 50.0]
    x_train, y_train, x_test, y_test = train_test_split(x, y,seed = 666);
    reg = SimpleLinearRegression()
    reg.fit(x_train,y_train)
    print(reg.a_)
    print(reg.b_)
    plt.scatter(x_train,y_train)
    plt.plot(x_train,reg.predict(x_train),color ='r')
    plt.show()
    predict_y = reg.predict(x_test)
    print(mean_squared_error(predict_y,y_test))
    print(mean_absolute_error(predict_y,y_test))
    print(root_mean_squared_error(predict_y,y_test))

R Squared
$R^2 = 1- \frac {ss_{residual}}{SStotal}$
$R^2 = 1 - \frac {\sum_i (\hat {y} ^{(i)}-y^{(i)})^2}{\sum_i(\hat{y} - y^{(i)})^2}$

使用我们的模型预测产生的错误

使用 y = $\hat y$ 预测产生的错误
Baseline Model

R^2 <= 1
$R^2$ 越大越好。当我们的预测模型不犯任何错误, $R^2$ 得到最大值1
当我们的模型等于基准模型时, $R^2$ 为 0
如果 $R^2$ < 0,说明我们学习到的模型还不如基准模型。此时,很有可能我们的数据不存在任何线性关系
$R^2 = 1 - \frac {\sum_i (\hat {y} ^{(i)}-y^{(i)})^2/m}{\sum_i(\hat{y} - \bar y)/m} →1 - \frac {MSE(\hat y,y)}{Var(y)}$

def r_Squared(y_true,y_predict):
    assert len(y_true) == len(y_predict), \
        "the size of y_true must be equal to the size of y_predict"
    return 1- (mean_squared_error(y_true,y_predict) / np.var(y_true))

posted @ 2019-12-15 14:23 caomaoboy 阅读(1077) 评论(0) 收藏举报

刷新页面返回顶部

caomaoboy

机器学习(二)-一元线性回归算法(代码实现及数学证明)

评测标准

公告