并查集

• 并查集子节点纸箱父节点
• 判断网络中连接的状态
  • 网络是个抽象概念:用户之间形成的网络(好友之间,音乐之间,图书之间,路由器之间,交通网络)

public interface UF {
    int getSize() ;
    //查看2个元素是否相连的
    boolean isConnected (int p,int q);
    //将2个元素放在一起
    void unionElements(int p,int q);
}

public class UnionFind1 implements  UF {
    private int[] id;
    public UnionFind1(int size){
        id =new int[size];
        for(int i =0;i<id.length;i++)
            id[i] = i;
    }
    @Override
    public int getSize() {
        return id.length;
    }

    @Override
    public boolean isConnected(int p, int q) {
        return (find(p) ==find(q));
    }

    @Override
    public void unionElements(int p, int q) {
        int pId =find(p);
        int qId = find(q);
        for (int i = 0;i<id.length;i++)
            if(id[i] == pId)
                id[i] = qId;
    }
    private int find(int p){
        if(p<0 && p>=id.length)
            throw  new IllegalArgumentException("index out of bound.");
        return id[p];
    }


}

unionElements	O(N)
isConnected	O(1)

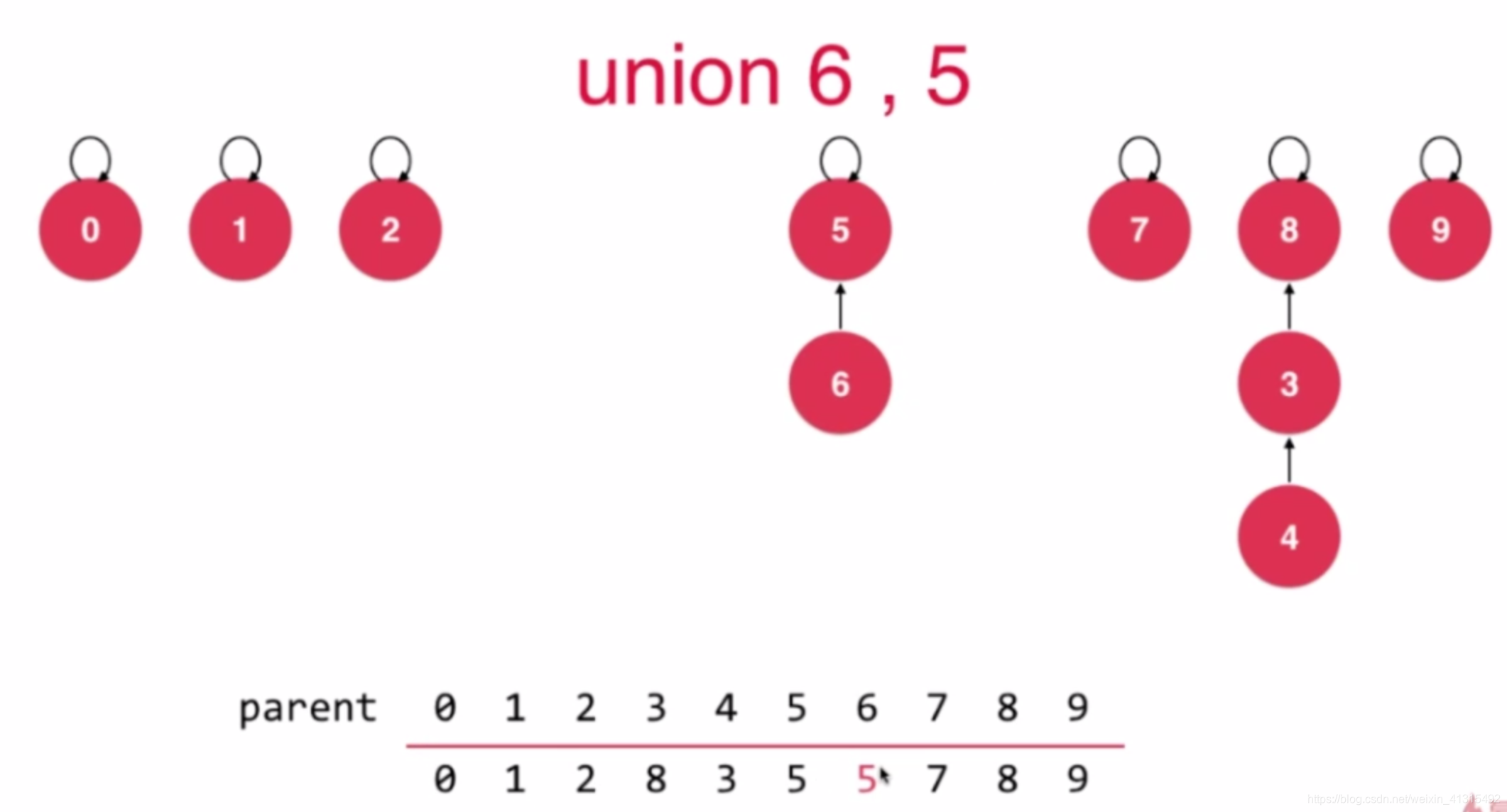
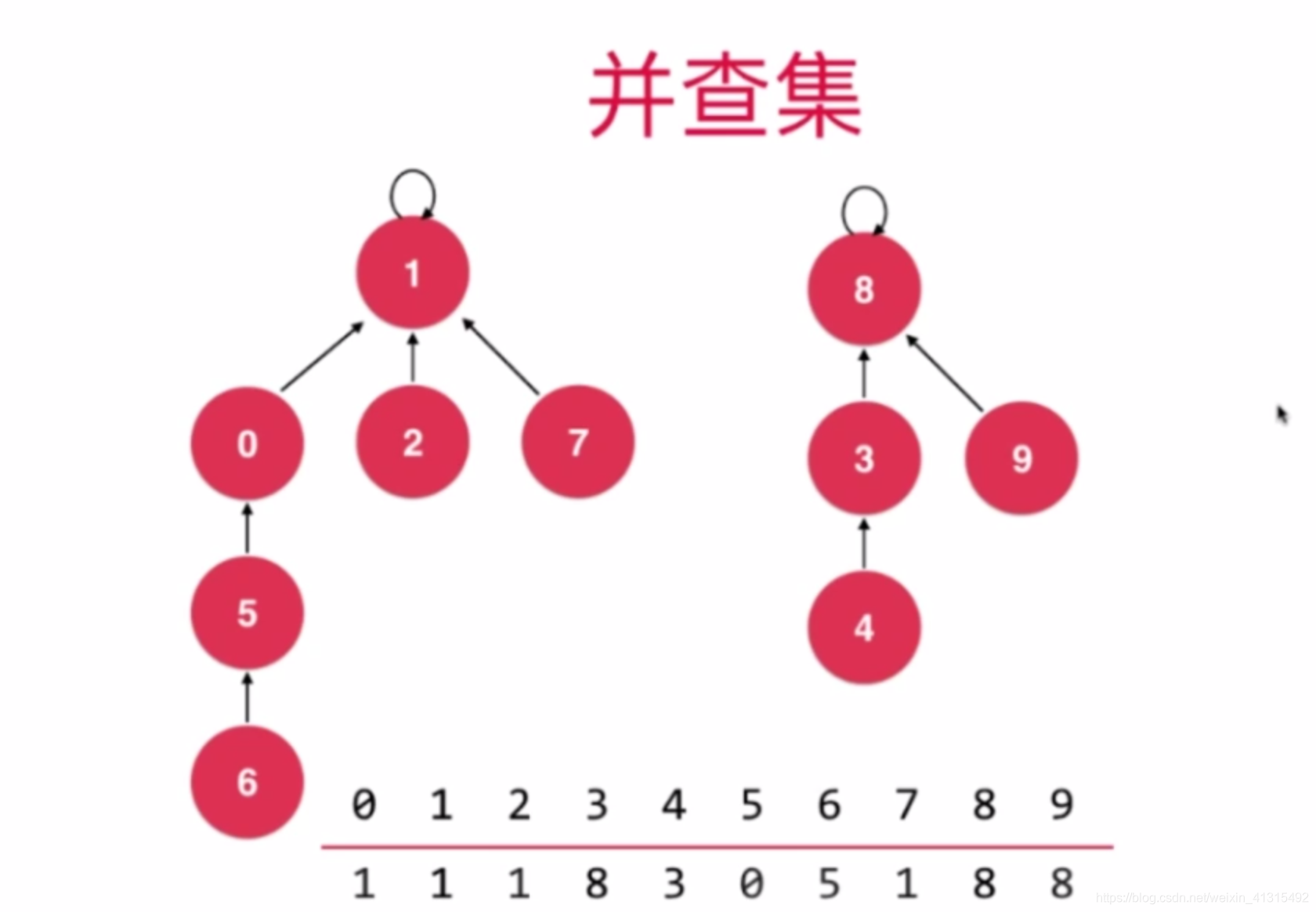
并查集 通过一个数组去记录 这些节点之间的关系:
举个比较容易理解的例子 假设 向以前抗战时期 中共地下党 之间的间谍他们为了防止中间出现叛徒 即使属于同一个组织 但是也不一定认识 但是每个人 都会有一个联络人 有一个代号 通过暗号交流 要交接任务只能联系上级 只有职位比较高的 才能知道地下和他联系的一级联络人 但是 即便这样 他下级的再下一级很多情况下也是没法知道的 因为地下党也可以自己发展下线而领导可能只知道有这么个人 只能通过一级一级的向上汇报之间的工作。
类比 并查集 也是类似的 数组 有数组索引(代号) 然后数组存储的值 就是别的数组的 索引(代号) a[长江] = 黄河 区别只是 在数组里面索引为 0,1,2,3的顺序数字 做下改变 令 长江为 0 黄河为1 就变成 a[0] = 1 a[1]=xxx
这样就形成了 关系之间的关联 。

public class UnionFind2 implements UF{
    private int[] parent;
    public  UnionFind2(int size){
        parent = new int[size];
        for (int i=0;i<parent.length;i++){
            parent[i] = i;
        }

    }

    @Override
    public int getSize() {
        return parent.length;
    }
    private int find(int p){
        if(p<0 && p>=parent.length)
            throw  new IllegalArgumentException("index out of bound.");
        //根节点 就是 索引和值都等于自己的 所以 如果索引何止不匹配就去找他的上级 复杂度O(h) h层数
        while(p!=parent[p])
            p =parent[p];
        return p;
    }

    @Override
    public boolean isConnected(int p, int q) {
        return find(p)==find(q);
    }

    @Override
    public void unionElements(int p, int q) {
        //找到 p最上面的节点
        int pRoor =find(p);
     	//找到 q最上面的节点
        int qRoot =find(q);
        //如果都在一个领导手下 那就不要合并了
        if(pRoor ==qRoot)
            return;
         //否则p合并到q的领导的下级去
        parent[pRoor] = qRoot;
    }
}

基于size优化

在合并的时候 看 如果 p的根节点 的数节点 远大于 q 的 根节点 那 向q合并 并 跟新q根节点子节点数量

//用来记录节点下的子节点数量
private int[] sz;
 @Override
    public void unionElements(int p, int q) {
        int pRoor =find(p);
        int qRoot =find(q);
        if(pRoor ==qRoot)
            return;
        if(sz[pRoor] <sz[qRoot]){
            parent[pRoor] = qRoot;
            sz[qRoot] += sz[pRoor];
        }else{
            parent[qRoot] =pRoor;
            sz[pRoor] += sz[qRoot];
        }

    }

基于rank 优化

private int[] rank;
@Override
    public void unionElements(int p, int q) {
        int pRoor =find(p);
        int qRoot =find(q);
        if(rank[pRoor] <rank[qRoot]){
            parent[pRoor] =qRoot;
        }else if(rank[pRoor] >rank[qRoot])
            parent[qRoot] =pRoor;
        else{
            parent[qRoot] =pRoor;
            rank[pRoor] += 1;
        }


    }

基于路径压缩

parent[p] = parent[parent[p]];