KMP算法
一、问题引入
BF算法的平均时间复杂度过高,提出了一种新的匹配算法 KMP算法。
主串S的位置i 一直往下移动,不再回溯。但字串T的位置j 需要根据算法确定下来。
二、解决过程
- 函数:get_next()
void get_next(const char *T, int **next)
{
int i = 0, j = -1;
int T_len = strlen(T);
(*next) = (int *)malloc(T_len * sizeof(int));
memset(*next, 0, T_len * sizeof(int));
(*next)[0] = -1;
while (i < T_len-1)
{
if (j == -1 || T[i] == T[j])
{
++i;
++j;
(*next)[i] = j;
}
else
j = (*next)[j];
}
// test
for (int i = 0; i < T_len; i++)
printf("%d\t", (*next)[i]);
printf("\n");
}
- 函数:index_kmp()
int index_kmp(const char *S, const char *T, int pos)
{
/* pos的有效范围:0<=pos<=S_len-1 */
int i = pos, j = 0;
int *next = NULL;
int S_len = strlen(S);
int T_len = strlen(T);
/* 串S和串T不为空串 */
if (S_len == 0 || T_len == 0)
return -1;
if (pos < 0 || pos > S_len)
return -1;
get_next(T, &next);
while (i < S_len && j < T_len)
{
printf("第%d轮: i=%d\tj=%d\n", ++count, i, j); // test
if (j == -1 || S[i] == T[j])
{
++i;
++j;
}
else
{
j = next[j];
}
}
free(next);
if (j >= T_len)
return i - T_len;
else
return -1;
}
- 函数:main()
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
int main(void)
{
char S[] = {"hello world"};
char T[] = {"ello"};
int index; // index从0开始
printf("S_String:%s\n", S);
printf("T_String:%s\n", T);
if (-1 == ( index = index_kmp(S, T, 0)))
{
printf("Not found\n");
}
else
{
printf("Found, index is %d\n", index);
}
return 0;
}
💡 运行结果



三、反思总结
3-1 重点看一下next的值


3-2 分析示例1
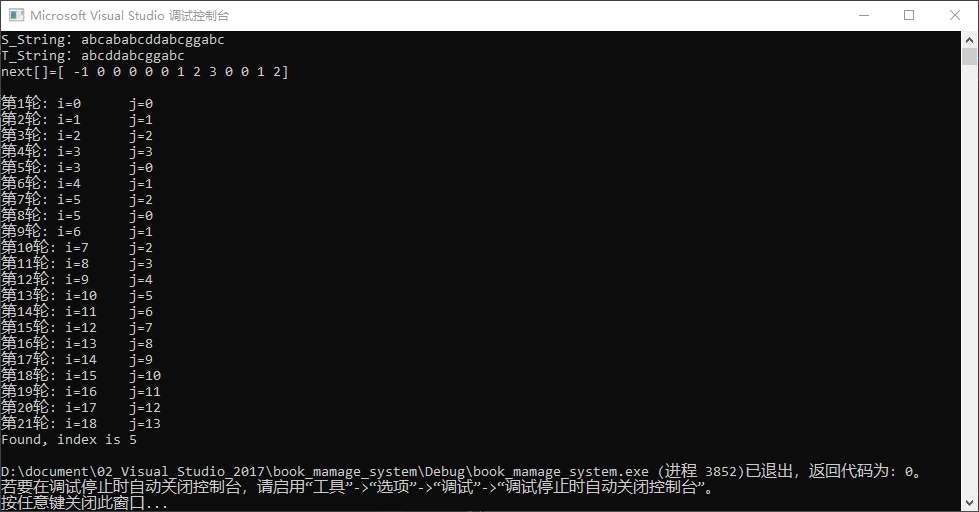
1️⃣ 第一大轮:
第1轮: i=0 j=0
第2轮: i=1 j=1
第3轮: i=2 j=2
第4轮: i=3 j=3
2️⃣ 第二大轮:
第5轮: i=3 j=0
第6轮: i=4 j=1
第7轮: i=5 j=2
3️⃣ 第三大轮:
第8轮: i=5 j=0
第9轮: i=6 j=1
第10轮: i=7 j=2
第11轮: i=8 j=3
第12轮: i=9 j=4
第13轮: i=10 j=5
第14轮: i=11 j=6
第15轮: i=12 j=7
第16轮: i=13 j=8
第17轮: i=14 j=9
第18轮: i=15 j=10
第19轮: i=16 j=11
第20轮: i=17 j=12
第21轮: i=18 j=13
3-3 分析示例2
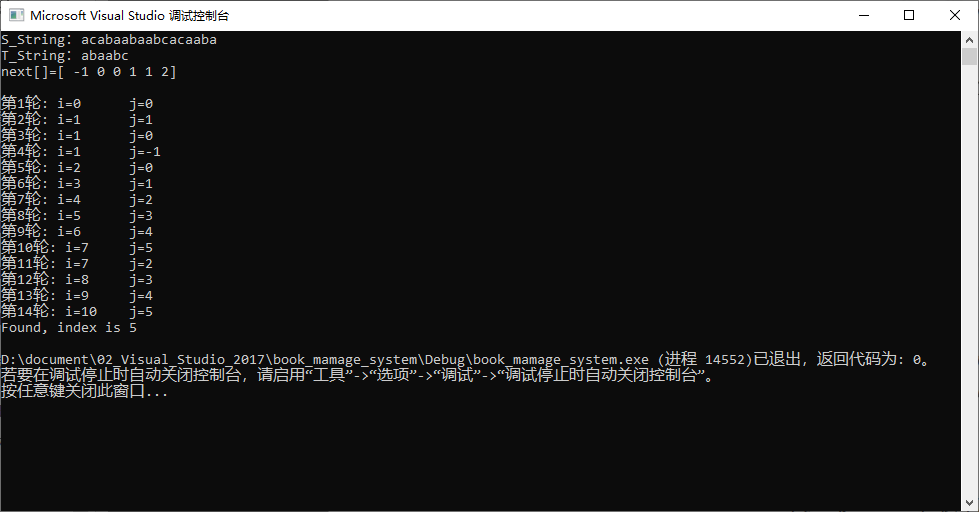
1️⃣ 第一大轮:
第1轮: i=0 j=0
第2轮: i=1 j=1
2️⃣ 第二大轮:
第3轮: i=1 j=0
3️⃣ 第三大轮:
第4轮: i=1 j=-1
第5轮: i=2 j=0
第6轮: i=3 j=1
第7轮: i=4 j=2
第8轮: i=5 j=3
第9轮: i=6 j=4
第10轮: i=7 j=5
第11轮: i=7 j=2
第12轮: i=8 j=3
第13轮: i=9 j=4
第14轮: i=10 j=5
3-4 示例3
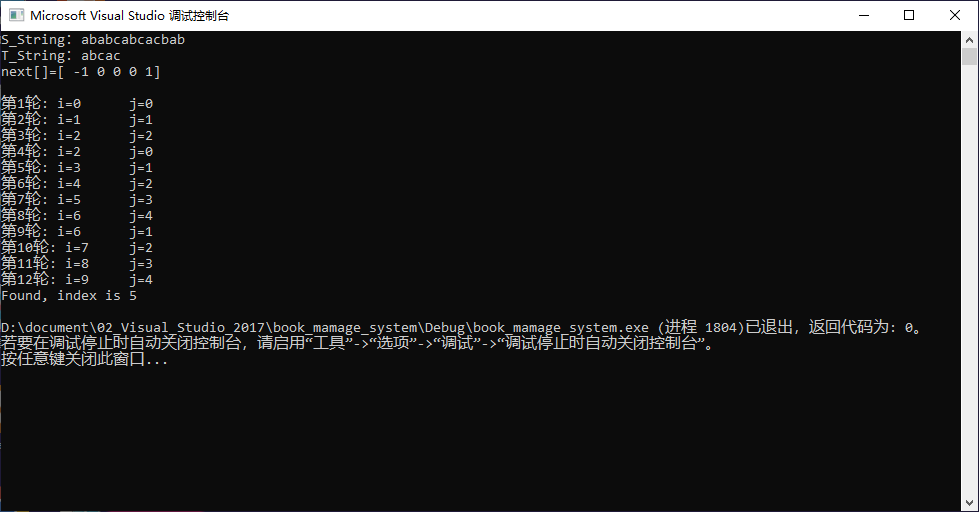
- 第一轮匹配过程

- 第二轮匹配过程

- 第三轮匹配过程

四、参考引用
数据结构第二版:C语言版 【严蔚敏】


 浙公网安备 33010602011771号
浙公网安备 33010602011771号