二叉树的实现：BSTree

一、树和二叉树

1-1 树的定义

翻译过来就是：树是由结点构成的，结点可以有也可以没有。若有结点，则肯定只有一个根结点。树是一种递归结构，俗称 “套娃”

1-2 二叉树的定义

翻译过来就是：二叉树是树的一个子集，每一个结点 至多 只能有两个结点（左结点和右结点）

二、二叉树的特性

2-1 二叉树的存储

二叉树的存储结构可以采用 顺序存储 和 链式存储 两种方式。下面示例采用链式存储结构实现

示例中，小小改动，其中名称和结点数据域变化

typedef struct BSTreeNode
{
	int    key;                 // 关键字(键值)
	struct BSTreeNode *left;    // 左孩子
	struct BSTreeNode *right;   // 右孩子
	struct BSTreeNode *parent;  // 父结点
}Node, *BSTree;

2-2 二叉树的遍历

遍历二叉树（traversing binary tree）是指按某条搜索路径巡访树中每一个结点，使得每一个结点均被访问一次，而且仅被访问一次。

“遍历” 是二叉树各种操作的基础，假设访问结点的具体操作不仅仅局限于输出结点数据域的值，而把 “访问” 延申到对结点的判别、计数等其他操作，可以解决一些关于而二叉树的其他实际问题。

根据访问限定先左后右，有3种访问情况，分别称之为 先（根）序遍历、中（根）序遍历和后（根）序遍历

注意：以集合的方式区分左子树和右子树，不能单纯的以左结点、右结点进行遍历

1️⃣ 先序遍历

若二叉树为空，则空操作；否则
1）访问根结点
2）先序遍历左子树
3）先序遍历右子树

2️⃣ 中序遍历

若二叉树为空，则空操作；否则
1）中序遍历左子树
2）访问根结点
3）中序遍历右子树

3️⃣ 后序遍历

若二叉树为空，则空操作；否则
1）后序遍历左子树
2）后序遍历右子树
3）访问根结点

示例图：

三、二叉树的实现

二叉树项目的主要功能有:

1）创建结点、插入结点、删除结点

2）查找数据域值最大的结点、查找数据域值最小的结点、查找指定数据域值的结点

3）先序遍历、中序遍历、后序遍历

4）查找指定数据域值的结点的前驱结点、查找指定数据域值的结点的后继结点

5）初始化二叉树、销毁二叉树

3-1 源码链接

由于源码篇幅过长，故不放在本页面，需要请访问博主的GitHub链接

• 遍历

/* 前序遍历 */
static void bstree_preorder(BSTree tree)
{
	if (tree != NULL)
	{
		printf("%d ", tree->key);
		bstree_preorder(tree->left);
		bstree_preorder(tree->right);
	}
}


/* 中序遍历 */
static void bstree_midorder(BSTree tree)
{
	if (tree != NULL)
	{ 
		bstree_midorder(tree->left);
		printf("%d ", tree->key);
		bstree_midorder(tree->right);
	}
}


/* 后序遍历 */
static void bstree_postorder(BSTree tree)
{
	if (tree != NULL)
	{
		bstree_postorder(tree->left);
		bstree_postorder(tree->right);
		printf("%d ", tree->key);
	}
}

• 查找结点

/* 查找key值最大的结点 */
static Node* bstree_node_maximum_find(BSTree tree)
{
	if (NULL == tree)
	{
		return NULL;
	}
	while (tree->right != NULL)
	{
		tree = tree->right;
	}
	return tree;
}

/* 查找key值最小的结点 */
static Node* bstree_node_minimum_find(BSTree tree)
{
	if (NULL == tree)
	{
		return NULL;
	}
	while (tree->left != NULL)
	{
		tree = tree->left;
	}
	return tree;
}

/* 递归查找法 通过指定key值搜索结点 */
static Node* bstree_node_search_with_key(BSTree tree, int key)
{
	if (NULL == tree || tree->key == key)
	{
		return tree;
	}
	if (key < tree->key)
	{
		return bstree_node_search_with_key(tree->left, key);
	}
	else
	{
		return bstree_node_search_with_key(tree->right, key);
	}
}

• 前驱结点和后继结点

注意：中序遍历--左子树-> 根 -> 右子树

前驱结点的定义：对二叉树进行 中序遍历 排序后，指定结点的前一个结点称之为前驱结点

后继结点的定义：对二叉树进行 中序遍历 排序后，指定结点的后一个结点称之为后继结点

/* 查找结点node的后继结点，即查找"二叉树中数据值大于该结点的最小结点" */
static Node* bstree_successor(Node *node)
{
	// 若该结点存在右孩子，则查找以右孩子为根结点二叉树的最小结点
	if (node->right != NULL)
	{
		return bstree_node_minimum_find(node->right);
	}
	// 若该结点没有右孩子。则该结点有两种可能：
	// 01) 该结点是一个左孩子，则该结点的后继结点就是它的父结点
	// 02) 该结点是一个右孩子，则查找该结点的最低父结点，且该父结点拥有左孩子，满足条件的最低父结点就是结点node的后继结点
	Node *p = node->parent;
	while (p != NULL && node == p->right)
	{
		node = p;
		p = p->parent;
	}
	return p;
}

/* 查找结点node的前驱结点，即查找"二叉树中数据值小于该结点的最大结点" */
static Node* bstree_predecessor(Node *node)
{
	// 若该结点存在左孩子，则查找以左孩子为根结点二叉树的最大结点
	if (node->left != NULL)
	{
		return bstree_node_maximum_find(node->left);
	}
	// 若该结点没有左孩子。则该结点有两种可能：
	// 01) 该结点是一个左孩子，则查找该结点的最低父结点，且该父结点拥有右孩子，满足条件的最低父结点就是结点的前驱结点
	// 02) 该结点是一个右孩子，则该结点的前驱结点就是它的父结点
	Node *p = node->parent;
	while (p != NULL && node == p->left)
	{
		node = p;
		p = p->parent;
	}
	return p;
}

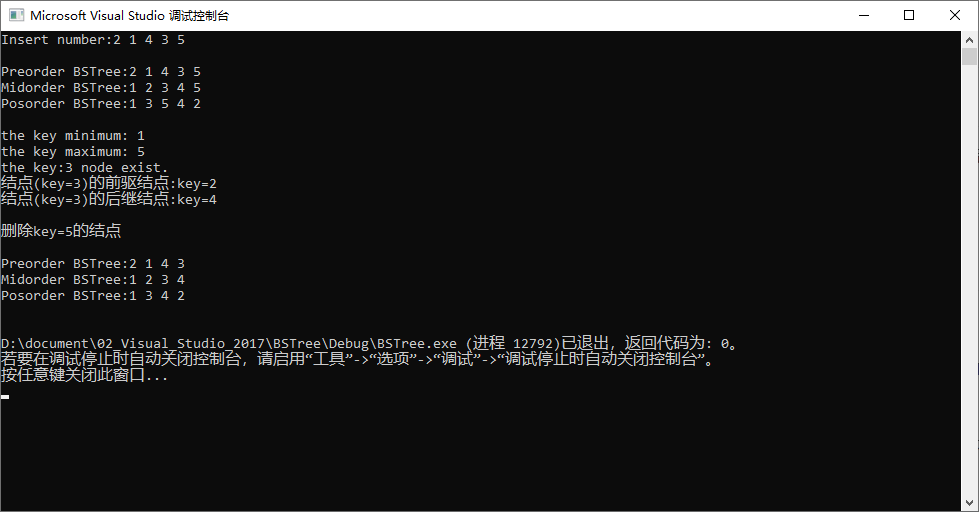
3-2 编译运行

四、参考来源

数据结构第二版：C语言版--【严蔚敏】 第五章 树和二叉树