Dancing Links 学习笔记
Dancing Links
本周的AI引论作业布置了一道数独
加了奇怪剪枝仍然TLE的Candy?不得不去学了dlx
dlxnb!
Exact cover
设全集X,X的若干子集的集合为S。精确覆盖是指,选择一个S的子集S‘,满足X中的每一个元素在S’中恰好出现一次。
是一个NPC问题。
可以表示成01矩阵形式,选择若干行,使得每一列恰好有且仅有一行为1.
Sudoku
数独可以转化为精确覆盖问题。
令N=81为数独中格子个数,则:
(x, y)=1表示(x,y)处填了数(x+N, z)=1表示x行填了z(y+N*2, z)=1表示y列填了z(r+N*3, z)=1表示r宫填了z
对于已经填了数的格子,转化为1行;
对于空的格子,转化为9行。
Algorithm X
一种显然的dfs:
- 就是选择某一列,再选择该列的为1的某一行。
- 删除该列(包括该列上为1的所有行)
- 删除该行(包括该行上为1的所有列)
一个显然的启发式优化:minimum-remaining-values(MRV) heuristic
- 优先选择节点个数(1的个数)少的列。
Dancing Links
Dancing links is the technique suggested by Donald Knuth to efficiently implement his Algorithm X.
是一种用来高效实现algorithm X的数据结构。
就是“交叉十字循环双向链表”。
第0行分别是root和每一列的列首节点
其他的只有为1的位置才有节点。
删除某一列时,只要处理该列首节点(包括其左右节点)的左右指针;
删除某列时同时要删除该列上为1的所有行;
删除某一行时,只要处理该行所有节点(包括其上下节点)的上下指针。
值得注意的是,删除之后该列/行的结构没有改变。
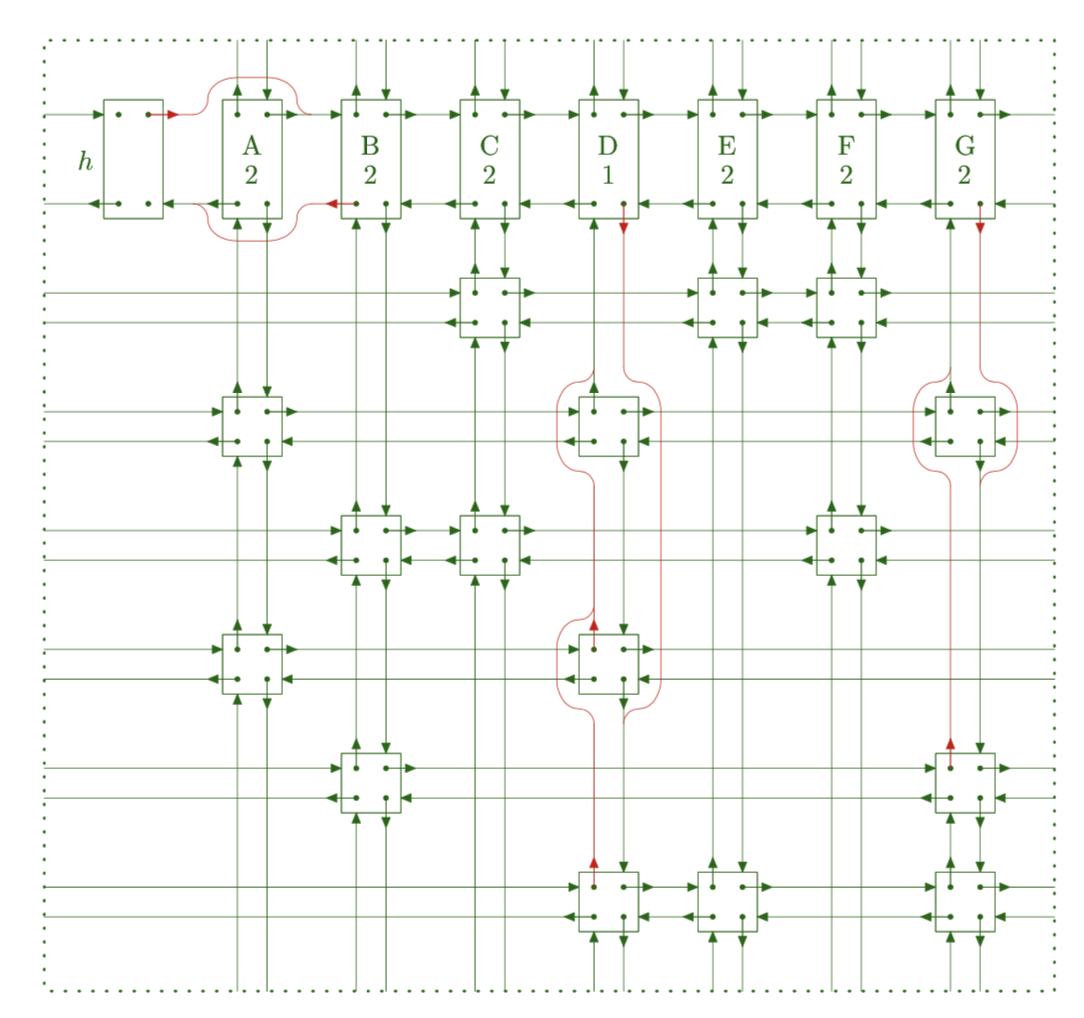
实现细节
每个节点维护:
l r u d左右上指针col列指针row行标号cnt保存该列的元素个数(只列首/用来MRV优化)
a和h数组保存列首/行首节点指针
初始化init
- 处理列首
在矩阵(r,c)位置加入一个元素/1 link
- 加在
a[c]下,h[r]右 - (实际的“线”是不是直的不重要
删除某列del
- 删除该列,以及该列上的所有行
恢复某列add
- 按删除相反的顺序恢复
主过程dance
-
root->r == root时完成 -
选择元素最少的某列
c并删除该列(包括该列上为1的所有行) -
选择该列上为1的某行,删除该行(包括该行上为1的所有列)
实际上这一行在2中已经删除了,只要处理该行的列即可
-
递归搜索
-
恢复该行
-
恢复该列
注意
- del/add时处理个数是必要的,因为那一行所对应的列不一定会被删去
- 恢复要按照删除的逆序
代码
POJ 3076 16*16数独问题的代码
结构体版太丑了还是放指针版吧QwQ
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#include <ctime>
using namespace std;
const int NUM = 260*4*16, N = 260*16, K = 16, L = 4, M = N*16;
int n = 256*4, num = 256, m=0;
struct meow {
meow *l, *r, *u, *d, *col;
int row;
int cnt;
} pool[NUM];
meow *a[NUM], *h[M], *root;
int ans[N], sz;
char s[20][20];
struct action {
int x, y, z;
} q[M];
void init() {
for(int i=0; i<=n; i++) a[i] = &pool[i];
for(int i=0; i<=n; i++) {
a[i]->l = a[i-1];
a[i]->r = a[i+1];
a[i]->u = a[i]->d = a[i];
a[i]->col = a[i];
a[i]->row = 0;
a[i]->cnt = 0;
}
a[0]->l = a[n]; a[n]->r = a[0];
root = a[0];
sz = n;
memset(h, 0, sizeof(h));
}
void link(int r, int c) {
sz++;
meow *x = a[sz] = &pool[sz];
x->row = r;
x->col = a[c];
a[c]->cnt++;
x->d = a[c]->d; x->d->u = x;
x->u = a[c]; x->u->d = x;
if(h[r] == NULL) {
h[r] = x->l = x->r = x;
}
else {
x->r = h[r]->r; x->r->l = x;
x->l = h[r]; x->l->r = x;
}
}
void del(meow *x) {
x->l->r = x->r;
x->r->l = x->l;
for(meow *i = x->d; i != x; i = i->d)
for(meow *j = i->r; j != i; j = j->r) {
j->d->u = j->u;
j->u->d = j->d;
j->col->cnt--;
}
}
void add(meow *x) {
x->l->r = x->r->l = x;
for(meow *i = x->u; i != x; i = i->u)
for(meow *j = i->l; j != i; j = j->l) {
j->u->d = j->d->u = j;
j->col->cnt++;
}
}
bool dance(int k) {
if(root->r == root) {
for(int i=1; i<=num; i++) {
action &x = q[ans[i]];
s[x.x][x.y] = 'A' + x.z-1;
}
return true;
}
meow *c = root; c->cnt = 1e9;
for(meow *x = root->r; x != root; x = x->r)
if(x->cnt < c->cnt) c = x;
del(c);
for(meow *i = c->d; i != c; i = i->d) {
ans[k+1] = i->row;
for(meow *j = i->r; j != i; j = j->r) del(j->col);
if(dance(k+1)) return true;
for(meow *j = i->l; j != i; j = j->l) add(j->col);
}
add(c);
return false;
}
inline int grid_id(int x, int y, int k=L) {return (x-1)/k*k + (y-1)/k+1;}
void sudoku(int x, int y, int z) {
m++;
link(m, (x-1)*K+y);
link(m, (x-1)*K+z + num);
link(m, (y-1)*K+z + num*2);
link(m, (grid_id(x, y)-1)*K+z + num*3);
q[m] = (action) {x, y, z};
}
int main() {
while(scanf("%s", s[1]+1) != EOF) {
init();
for(int i=1; i<=K; i++) {
for(int j=1; j<=K; j++) {
int a;
if(s[i][j] == '-') a = 0;
else a = s[i][j]-'A'+1;
if(a != 0) sudoku(i, j, a);
else for(int k=1; k<=K; k++) sudoku(i, j, k);
}
if(i != K) scanf("%s", s[i+1]+1);
}
dance(0);
for(int i=1; i<=K; i++) {
for(int j=1; j<=K; j++) printf("%c", s[i][j]);
puts("");
}
puts("");
}
}
Copyright:http://www.cnblogs.com/candy99/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号