CF37C Old Berland Language 题解

洛谷传送门

CF 传送门

题意

构造 \(n\) 个 01 字符串，使得它们的长度依次为 \(len_1,len_2,\ldots len_n\)，并且不存在一个字符串是另一个字符串的前缀。

输出这 \(n\) 个字符串，或指出无解。

思路

学过哈夫曼编码的同学应该知道，这题等价于：构造一颗二叉树，使得它有 \(n\) 个叶子，并且每个叶子的深度（从 0 开始）为 \(len_1\) 到 \(len_n\)。

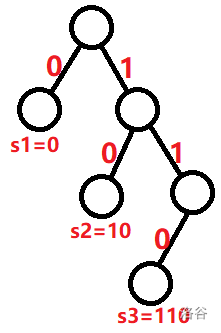
如图（样例1），若将除了叶节点的每个节点，左儿子标上 0，右儿子标上 1，则从根到每个叶结点的路径上经过的数连起来，就是这个叶节点对应的字符串。

那问题就变得简单了很多，只要在满二叉树上进行dfs遍历，碰到深度为 \(len_1\) 到 \(len_n\) 中某一个的节点，就把这个节点当成叶结点，并记录答案，不继续向下递归。

若递归结束还有一些 \(len\) 没有答案，就输出 NO。

我用的是栈存每个 \(len\) 对应的答案位置，所以代码比较简短，也顺利拿下洛谷最优解。

代码

#include <bits/stdc++.h>
using namespace std;
int n,sum;//sum记录有多少个len有答案了 
stack<int>p[1005];
string ans[1005];
void dfs(string s){
	int len=s.length();//字符串的长度就是深度
	if(!p[len].empty()){//这个深度存在某个len没有答案 
		ans[p[len].top()]=s;//记录答案 
		p[len].pop(),sum++;
		if(sum==n){//找到了全部的答案 
			printf("YES\n"); 
			for(int i=1;i<=n;i++) cout<<ans[i]<<"\n";
			exit(0);
		}
		return;
	}
	dfs(s+"0");dfs(s+"1");//向下递归
}
int main(){
	scanf("%d",&n);
	for(int i=1,len;i<=n;i++){
		scanf("%d",&len);
		p[len].push(i);
	}
	dfs("");
	printf("NO\n");//递归结束也没有找到全部答案 
	return 0;
}