Leetcode刷题 - 动态规划

322. Coin Change

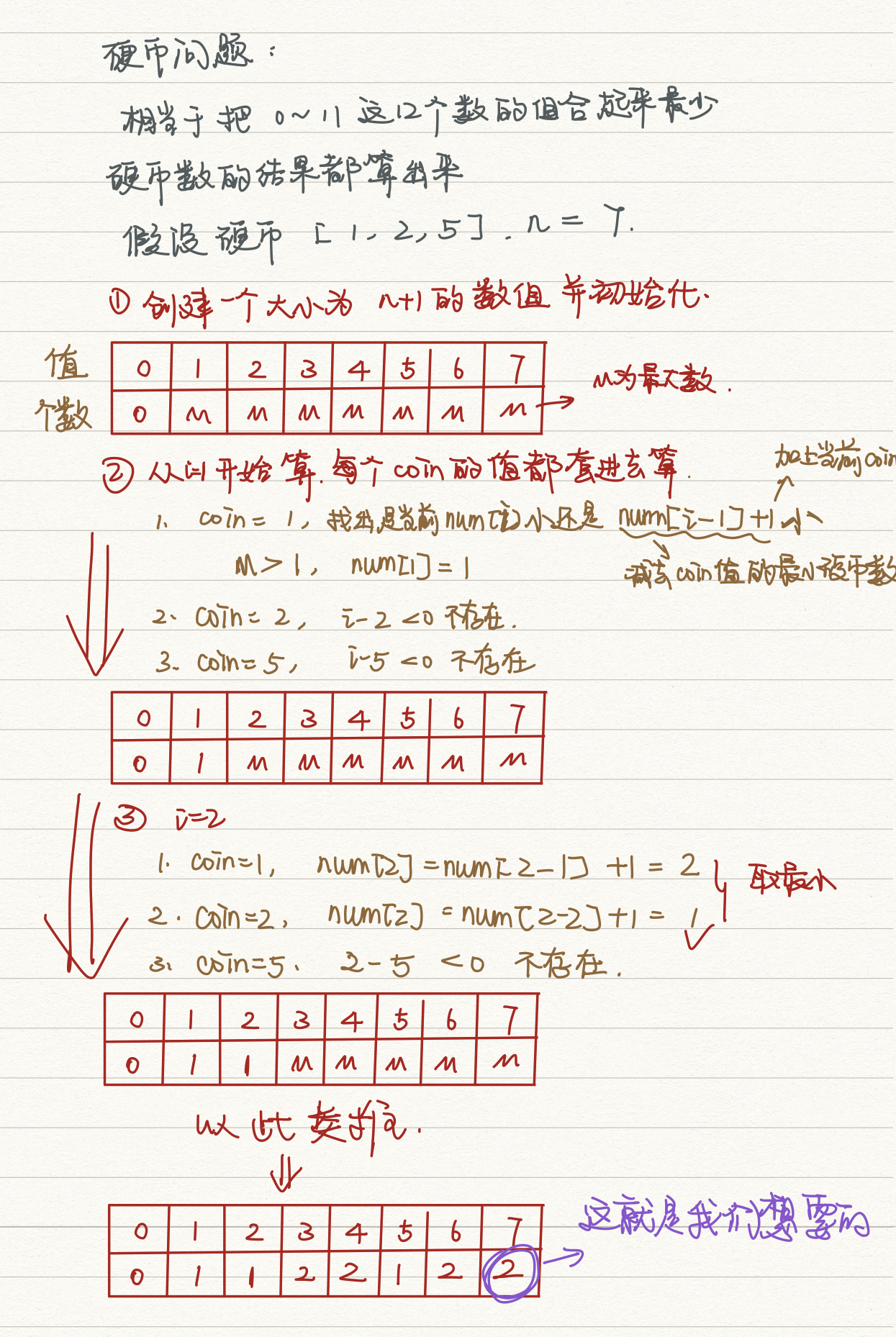
class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //动态规划
        // 最优解法
        // 算出1-11每个数的组成需要的最少硬币数
        int nums[amount+1];
        nums[0] = 0;
        
        // sort coins
        sort(coins.begin(), coins.end());
        // 每个子问题的求解
        for (int i = 1; i <= amount; i ++){
            nums[i] = INT_MAX;
            for (int val : coins){
                if (i - val < 0) break;
                if(nums[i-val] != INT_MAX) nums[i] = min(nums[i], nums[i - val] + 1);
            }
        }
        return nums[amount] == INT_MAX ? -1 : nums[amount];
    }
};

518. Coin Change 2

这道题与前面一道不同的是需要找到所有可能的组合数，所以要先从硬币的值着手。

• 从第一个硬币开始，找到 1 ~ amount里这个硬币可以组合的数，若是1，则每个数由1组成的方法只有1种，
• 从第二个硬币开始，循环 i = 0 ~ amount， 找到 i-val 可以组成的方案再加上自己本身可以组成的方案。
• 直到循环完所有的硬币，找到所有可能组成的方案后, nums[amount]就是我们要的值

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        
        if (amount == 0) return 1;
        if (coins.size() == 0) return 0;
        // 动态规划
        // 建立一个大小为amount+1的数组
        // 需要算有多少组合，从每个coin来看。
        // 在1-amount里，单独一个coin可能组成的方案有多少个
        // 再loop coins，找到两个组合在一起有多少方案
        int nums[amount+1];
        // 初始化里面为0
         memset(nums,0,sizeof(nums));
        // 初始化第一个元素为1，因为算上自己也算一种方案
        nums[0] = 1;
        sort(coins.begin(), coins.end());
        for (int val:coins){
            for (int i = val; i <= amount; i ++){
                nums[i] += nums[i - val];
            }
        }
        return nums[amount];
    }
};

　　

 

参考资料

1. https://leetcode.com/problems/coin-change/discuss/778548/C%2B%2B-DP-solution-explained-~100-Time-100-Space
2. https://leetcode.com/problems/coin-change-2/