R语言与概率统计(三) 多元统计分析(中)
模型修正
#但是,回归分析通常很难一步到位,需要不断修正模型
###############################6.9通过牙膏销量模型学习模型修正
toothpaste<-data.frame(
X1=c(-0.05, 0.25,0.60,0, 0.25,0.20, 0.15,0.05,-0.15, 0.15,
0.20, 0.10,0.40,0.45,0.35,0.30, 0.50,0.50, 0.40,-0.05,
-0.05,-0.10,0.20,0.10,0.50,0.60,-0.05,0, 0.05, 0.55),
X2=c( 5.50,6.75,7.25,5.50,7.00,6.50,6.75,5.25,5.25,6.00,
6.50,6.25,7.00,6.90,6.80,6.80,7.10,7.00,6.80,6.50,
6.25,6.00,6.50,7.00,6.80,6.80,6.50,5.75,5.80,6.80),
Y =c( 7.38,8.51,9.52,7.50,9.33,8.28,8.75,7.87,7.10,8.00,
7.89,8.15,9.10,8.86,8.90,8.87,9.26,9.00,8.75,7.95,
7.65,7.27,8.00,8.50,8.75,9.21,8.27,7.67,7.93,9.26)
)
plot(toothpaste)#先画出三点图观察变量之间的关系
cor(toothpaste)
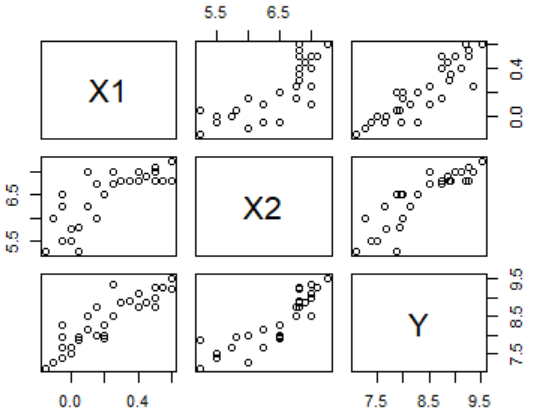
> lm.sol<-lm(Y~X1+X2,data=toothpaste)
> summary(lm.sol)
Call:
lm(formula = Y ~ X1 + X2, data = toothpaste)
Residuals:
Min 1Q Median 3Q Max
-0.49779 -0.12031 -0.00867 0.11084 0.58106
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.4075 0.7223 6.102 1.62e-06 ***
X1 1.5883 0.2994 5.304 1.35e-05 ***
X2 0.5635 0.1191 4.733 6.25e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2383 on 27 degrees of freedom
Multiple R-squared: 0.886, Adjusted R-squared: 0.8776
F-statistic: 105 on 2 and 27 DF, p-value: 1.845e-13
> lm.new<-update(lm.sol, .~.+I(X2^2)) #.~.表示原来的Y~X1+X2,+I(X2^2)多加了一个平方项
> summary(lm.new)
Call:
lm(formula = Y ~ X1 + X2 + I(X2^2), data = toothpaste)
Residuals:
Min 1Q Median 3Q Max
-0.40330 -0.14509 -0.03035 0.15488 0.46602
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 17.3244 5.6415 3.071 0.00495 **
X1 1.3070 0.3036 4.305 0.00021 ***
X2 -3.6956 1.8503 -1.997 0.05635 .
I(X2^2) 0.3486 0.1512 2.306 0.02934 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2213 on 26 degrees of freedom
Multiple R-squared: 0.9054, Adjusted R-squared: 0.8945
F-statistic: 82.94 on 3 and 26 DF, p-value: 1.944e-13
> confint(lm.new)
2.5 % 97.5 %
(Intercept) 5.72818421 28.9205529
X1 0.68290927 1.9310682
X2 -7.49886317 0.1076898
I(X2^2) 0.03786354 0.6593598
> #x2可能为0,考虑去掉
> lm2.new<-update(lm.new, .~.-X2)
> summary(lm2.new)
Call:
lm(formula = Y ~ X1 + I(X2^2), data = toothpaste)
Residuals:
Min 1Q Median 3Q Max
-0.4859 -0.1141 -0.0046 0.1053 0.5592
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.07667 0.35531 17.102 5.17e-16 ***
X1 1.52498 0.29859 5.107 2.28e-05 ***
I(X2^2) 0.04720 0.00952 4.958 3.41e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2332 on 27 degrees of freedom
Multiple R-squared: 0.8909, Adjusted R-squared: 0.8828
F-statistic: 110.2 on 2 and 27 DF, p-value: 1.028e-13
> #考虑两个变量之间不独立
> lm3.new<-update(lm2.new, .~.+X1*X2-X2)
> summary(lm3.new)
Call:
lm(formula = Y ~ X1 + I(X2^2) + X1:X2, data = toothpaste)
Residuals:
Min 1Q Median 3Q Max
-0.48652 -0.11434 -0.00502 0.10524 0.55927
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.076101 0.364641 16.663 2.15e-15 ***
X1 1.573061 3.667273 0.429 0.671
I(X2^2) 0.047219 0.009786 4.825 5.33e-05 ***
X1:X2 -0.007064 0.536935 -0.013 0.990
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2377 on 26 degrees of freedom
Multiple R-squared: 0.8909, Adjusted R-squared: 0.8783
F-statistic: 70.76 on 3 and 26 DF, p-value: 1.234e-12
逐步回归


#########################6.10逐步回归
cement<-data.frame(
X1=c( 7, 1, 11, 11, 7, 11, 3, 1, 2, 21, 1, 11, 10),
X2=c(26, 29, 56, 31, 52, 55, 71, 31, 54, 47, 40, 66, 68),
X3=c( 6, 15, 8, 8, 6, 9, 17, 22, 18, 4, 23, 9, 8),
X4=c(60, 52, 20, 47, 33, 22, 6, 44, 22, 26, 34, 12, 12),
Y =c(78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5,
93.1,115.9, 83.8, 113.3, 109.4)
)
plot(cement)
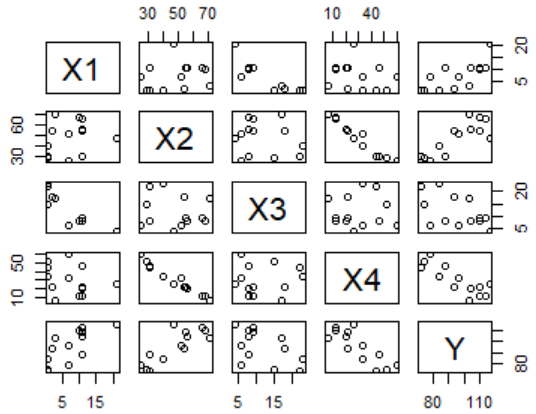
> lm.sol<-lm(Y ~ X1+X2+X3+X4, data=cement)
> summary(lm.sol)
Call:
lm(formula = Y ~ X1 + X2 + X3 + X4, data = cement)
Residuals:
Min 1Q Median 3Q Max
-3.1750 -1.6709 0.2508 1.3783 3.9254
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.4054 70.0710 0.891 0.3991
X1 1.5511 0.7448 2.083 0.0708 .
X2 0.5102 0.7238 0.705 0.5009
X3 0.1019 0.7547 0.135 0.8959
X4 -0.1441 0.7091 -0.203 0.8441
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.446 on 8 degrees of freedom
Multiple R-squared: 0.9824, Adjusted R-squared: 0.9736
F-statistic: 111.5 on 4 and 8 DF, p-value: 4.756e-07
> lm.step<-step(lm.sol)
Start: AIC=26.94
Y ~ X1 + X2 + X3 + X4
Df Sum of Sq RSS AIC
- X3 1 0.1091 47.973 24.974
- X4 1 0.2470 48.111 25.011
- X2 1 2.9725 50.836 25.728
<none> 47.864 26.944
- X1 1 25.9509 73.815 30.576
Step: AIC=24.97
Y ~ X1 + X2 + X4
Df Sum of Sq RSS AIC
<none> 47.97 24.974
- X4 1 9.93 57.90 25.420
- X2 1 26.79 74.76 28.742
- X1 1 820.91 868.88 60.629
>
> summary(lm.step)
Call:
lm(formula = Y ~ X1 + X2 + X4, data = cement)
Residuals:
Min 1Q Median 3Q Max
-3.0919 -1.8016 0.2562 1.2818 3.8982
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 71.6483 14.1424 5.066 0.000675 ***
X1 1.4519 0.1170 12.410 5.78e-07 ***
X2 0.4161 0.1856 2.242 0.051687 .
X4 -0.2365 0.1733 -1.365 0.205395
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.309 on 9 degrees of freedom
Multiple R-squared: 0.9823, Adjusted R-squared: 0.9764
F-statistic: 166.8 on 3 and 9 DF, p-value: 3.323e-08
> drop1(lm.step)
Single term deletions
Model:
Y ~ X1 + X2 + X4
Df Sum of Sq RSS AIC
<none> 47.97 24.974
X1 1 820.91 868.88 60.629
X2 1 26.79 74.76 28.742
X4 1 9.93 57.90 25.420
> lm.opt<-lm(Y ~ X1+X2, data=cement); summary(lm.opt)
Call:
lm(formula = Y ~ X1 + X2, data = cement)
Residuals:
Min 1Q Median 3Q Max
-2.893 -1.574 -1.302 1.363 4.048
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.57735 2.28617 23.00 5.46e-10 ***
X1 1.46831 0.12130 12.11 2.69e-07 ***
X2 0.66225 0.04585 14.44 5.03e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.406 on 10 degrees of freedom
Multiple R-squared: 0.9787, Adjusted R-squared: 0.9744
F-statistic: 229.5 on 2 and 10 DF, p-value: 4.407e-09
> library(car)#多重共线性,vif方差膨胀因子
> vif(lm.opt)
X1 X2
1.055129 1.055129
> sqrt(vif(lm.opt))>2#problem?若存在共线性怎么办?
X1 X2
FALSE FALSE
> AIC(lm.sol,lm.opt)
df AIC
lm.sol 6 65.83669
lm.opt 4 64.31239
> BIC(lm.sol,lm.opt)
df BIC
lm.sol 6 69.22639
lm.opt 4 66.57219
做线性回归要做:t检验,F检验,残差分析,模型解释(灵敏度分析)
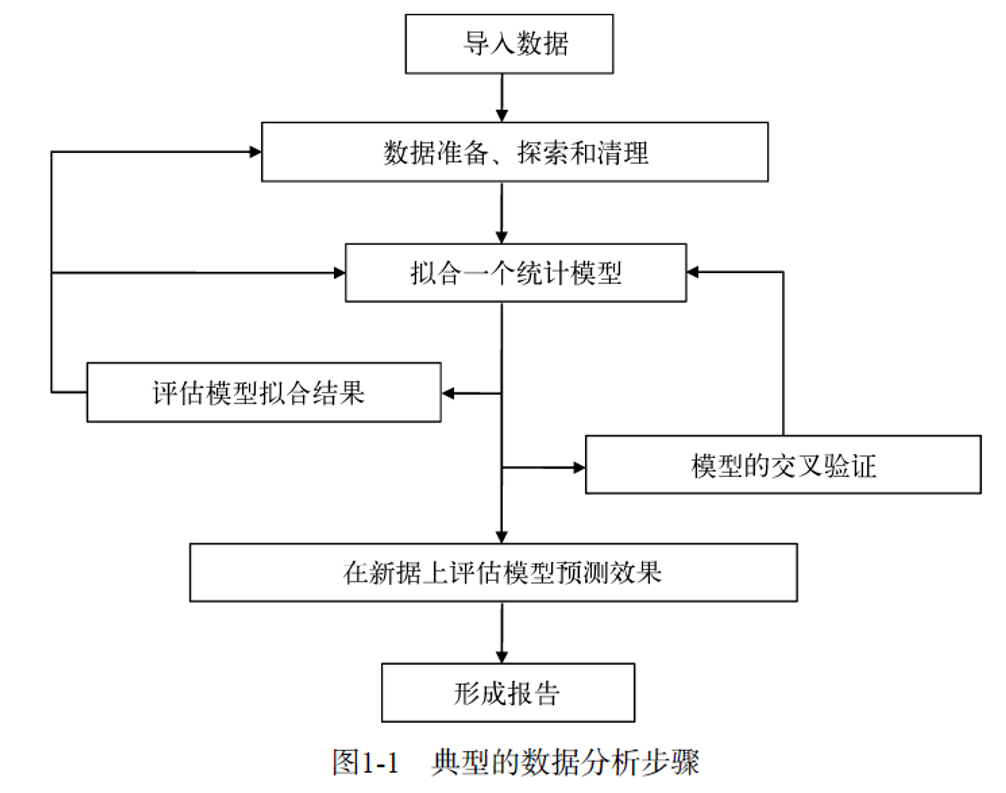
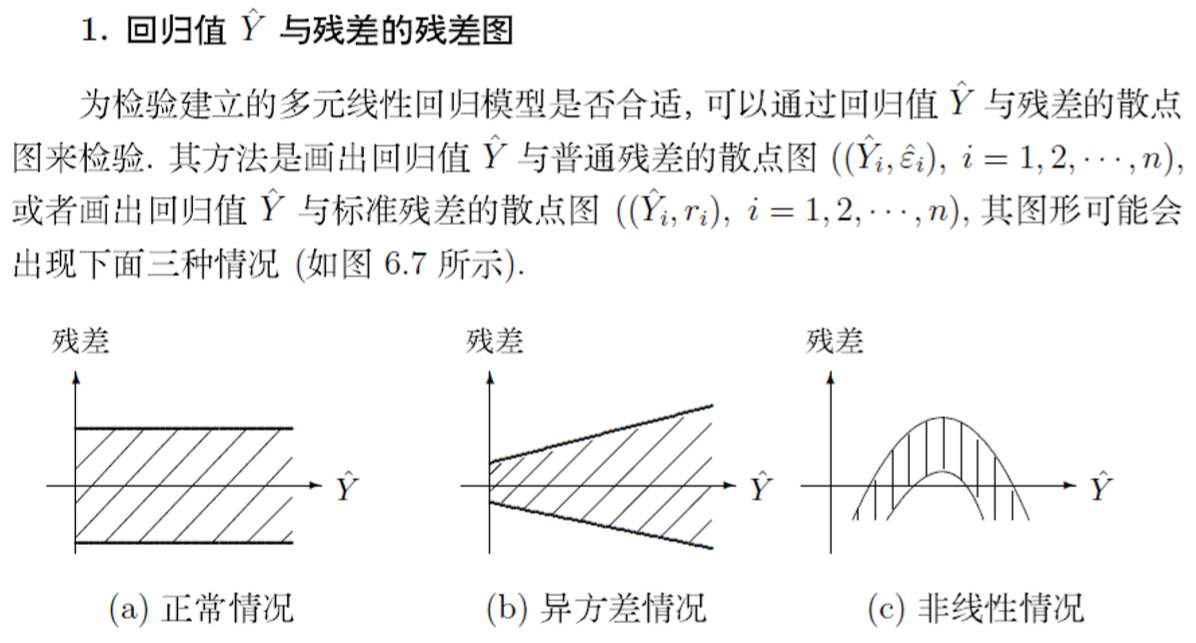
残差分析(回归诊断)


> ######6.5forbes数据分析的残差分析
> X<-matrix(c(
+ 194.5, 20.79, 1.3179, 131.79,
+ 194.3, 20.79, 1.3179, 131.79,
+ 197.9, 22.40, 1.3502, 135.02,
+ 198.4, 22.67, 1.3555, 135.55,
+ 199.4, 23.15, 1.3646, 136.46,
+ 199.9, 23.35, 1.3683, 136.83,
+ 200.9, 23.89, 1.3782, 137.82,
+ 201.1, 23.99, 1.3800, 138.00,
+ 201.4, 24.02, 1.3806, 138.06,
+ 201.3, 24.01, 1.3805, 138.05,
+ 203.6, 25.14, 1.4004, 140.04,
+ 204.6, 26.57, 1.4244, 142.44,
+ 209.5, 28.49, 1.4547, 145.47,
+ 208.6, 27.76, 1.4434, 144.34,
+ 210.7, 29.04, 1.4630, 146.30,
+ 211.9, 29.88, 1.4754, 147.54,
+ 212.2, 30.06, 1.4780, 147.80),
+ ncol=4, byrow=T,
+ dimnames = list(1:17, c("F", "h", "log", "log100")))
> forbes<-data.frame(X)
> plot(forbes$F, forbes$log100)#画出两个变量之间的散点图,观察是否存在线性趋势
> lm.sol<-lm(log100~F, data=forbes)
> summary(lm.sol)
Call:
lm(formula = log100 ~ F, data = forbes)
Residuals:
Min 1Q Median 3Q Max
-0.32261 -0.14530 -0.06750 0.02111 1.35924
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -42.13087 3.33895 -12.62 2.17e-09 ***
F 0.89546 0.01645 54.45 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.3789 on 15 degrees of freedom
Multiple R-squared: 0.995, Adjusted R-squared: 0.9946
F-statistic: 2965 on 1 and 15 DF, p-value: < 2.2e-16
> abline(lm.sol)#在散点图上添加直线

> #残差正态性检验 > y.res=residuals(lm.sol) > shapiro.test(y.res) Shapiro-Wilk normality test data: y.res W = 0.54654, p-value = 3.302e-06




所有代码:

#但是,回归分析通常很难一步到位,需要不断修正模型 ###############################6.9通过牙膏销量模型学习模型修正 toothpaste<-data.frame( X1=c(-0.05, 0.25,0.60,0, 0.25,0.20, 0.15,0.05,-0.15, 0.15, 0.20, 0.10,0.40,0.45,0.35,0.30, 0.50,0.50, 0.40,-0.05, -0.05,-0.10,0.20,0.10,0.50,0.60,-0.05,0, 0.05, 0.55), X2=c( 5.50,6.75,7.25,5.50,7.00,6.50,6.75,5.25,5.25,6.00, 6.50,6.25,7.00,6.90,6.80,6.80,7.10,7.00,6.80,6.50, 6.25,6.00,6.50,7.00,6.80,6.80,6.50,5.75,5.80,6.80), Y =c( 7.38,8.51,9.52,7.50,9.33,8.28,8.75,7.87,7.10,8.00, 7.89,8.15,9.10,8.86,8.90,8.87,9.26,9.00,8.75,7.95, 7.65,7.27,8.00,8.50,8.75,9.21,8.27,7.67,7.93,9.26) ) plot(toothpaste)#先画出三点图观察变量之间的关系 cor(toothpaste) lm.sol<-lm(Y~X1+X2,data=toothpaste) summary(lm.sol) #根据散点图做如下修正 lm.new<-update(lm.sol, .~.+I(X2^2)) #.~.表示原来的Y~X1+X2,+I(X2^2)多加了一个平方项 summary(lm.new) confint(lm.new) #x2可能为0,考虑去掉 lm2.new<-update(lm.new, .~.-X2) summary(lm2.new) #考虑两个变量之间不独立 lm3.new<-update(lm2.new, .~.+X1*X2-X2) summary(lm3.new) #########################6.10逐步回归 cement<-data.frame( X1=c( 7, 1, 11, 11, 7, 11, 3, 1, 2, 21, 1, 11, 10), X2=c(26, 29, 56, 31, 52, 55, 71, 31, 54, 47, 40, 66, 68), X3=c( 6, 15, 8, 8, 6, 9, 17, 22, 18, 4, 23, 9, 8), X4=c(60, 52, 20, 47, 33, 22, 6, 44, 22, 26, 34, 12, 12), Y =c(78.5, 74.3, 104.3, 87.6, 95.9, 109.2, 102.7, 72.5, 93.1,115.9, 83.8, 113.3, 109.4) ) plot(cement) lm.sol<-lm(Y ~ X1+X2+X3+X4, data=cement) summary(lm.sol) lm.step<-step(lm.sol) summary(lm.step) drop1(lm.step) lm.opt<-lm(Y ~ X1+X2, data=cement); summary(lm.opt) library(car)#多重共线性,vif方差膨胀因子 vif(lm.opt) sqrt(vif(lm.opt))>2#problem?若存在共线性怎么办? AIC(lm.sol,lm.opt) BIC(lm.sol,lm.opt) ######6.5forbes数据分析的残差分析 X<-matrix(c( 194.5, 20.79, 1.3179, 131.79, 194.3, 20.79, 1.3179, 131.79, 197.9, 22.40, 1.3502, 135.02, 198.4, 22.67, 1.3555, 135.55, 199.4, 23.15, 1.3646, 136.46, 199.9, 23.35, 1.3683, 136.83, 200.9, 23.89, 1.3782, 137.82, 201.1, 23.99, 1.3800, 138.00, 201.4, 24.02, 1.3806, 138.06, 201.3, 24.01, 1.3805, 138.05, 203.6, 25.14, 1.4004, 140.04, 204.6, 26.57, 1.4244, 142.44, 209.5, 28.49, 1.4547, 145.47, 208.6, 27.76, 1.4434, 144.34, 210.7, 29.04, 1.4630, 146.30, 211.9, 29.88, 1.4754, 147.54, 212.2, 30.06, 1.4780, 147.80), ncol=4, byrow=T, dimnames = list(1:17, c("F", "h", "log", "log100"))) forbes<-data.frame(X) plot(forbes$F, forbes$log100)#画出两个变量之间的散点图,观察是否存在线性趋势 lm.sol<-lm(log100~F, data=forbes) summary(lm.sol) abline(lm.sol)#在散点图上添加直线 #残差正态性检验 y.res=residuals(lm.sol) shapiro.test(y.res) y.res<-residuals(lm.sol);plot(y.res)#画出残差图 text(12,y.res[12], labels=12,adj=1.2) #或者 plot(lm.sol) plot(lm.sol,2)#残差的qq图 #异常值的判断 library(car) outlierTest(lm.sol) #去除异常值 i<-1:17; forbes12<-data.frame(X[i!=12, ]) lm12<-lm(log100~F, data=forbes12) summary(lm12) #残差正态性检验 y.res=residuals(lm12) shapiro.test(y.res)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号