欧拉函数

定义

（(Euler’s totient function)) 1∼N 中与N互质的数的个数被称为欧拉函数，记为 ϕ(N)。
比如说ϕ(1)=1。
比方说φ(8) = 4，因为1,3,5,7均和8互质。
当 n 是质数的时候，显然有ϕ(n)=n-1。

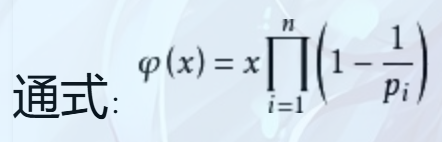
性质

1. ϕ(1)=1
2. 当 n 是质数的时候，ϕ(n)=n-1
3. 积性函数——若m,n互质，则ϕ(mn)=ϕ(m)ϕ(n)。

补充

1. 互质关系：如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。