raissi2019 算法思路和实现过程 （待更新...）

1. 神经网络的思路

前提条件：数据集
构造一个loss表达式
使用优化器最小化这个loss

2. 文章思路

需要求解的非线性偏微分方程的一般形式如下：
\(u_t+\mathcal{N}[u;\lambda] = 0,x\in \Omega,t\in[0,T]\) 其中，\(u\)是我们待求的解，\(\lambda\)是参数

我们可以利用神经网络求解两大类的问题：

1. data-driven solution：在\(\lambda\)已知的情况下求出PDE的解\(u(x,t)\)
2. data-driven discovery of partial differential equations：在\(\lambda\)未知的情况下求出PDE的解\(u(x,t)\)的同时确定参数\(\lambda\)的值

每类问题又分为连续型和离散型的情况。

2.1 \(\lambda\)已知

2.1.1 连续时间模型——非线性薛定谔方程

2.1.1.1 算法思路

由于研究范围涉及到了复数，为了方便编程，因此所有变量对应地有一个实部变量u和一个虚部变量v。

使用了多层感知机的神经网络，输入层和输出层各有两个神经元，中间有四个隐藏层，每层有100个神经元，如下图所示。

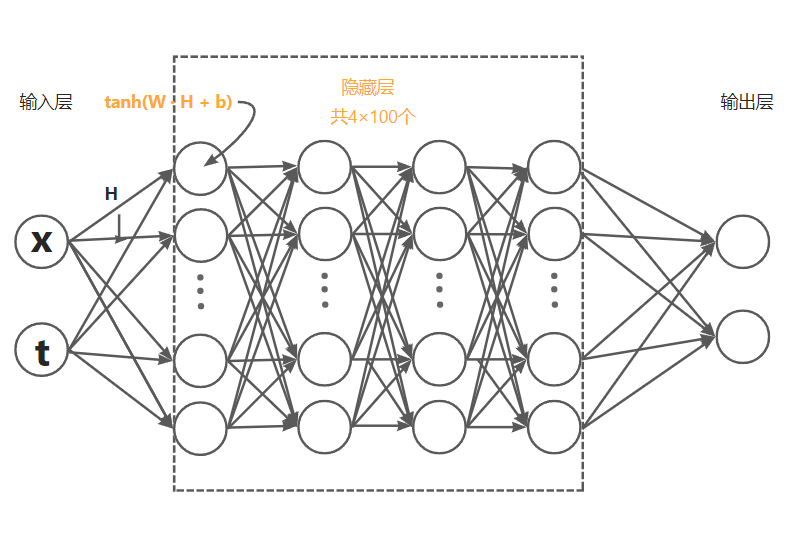
PINN将求解偏微分的问题转化成了一个参数优化问题，神经网络的权重weights和偏置biases就是需要优化的参数。我们的目的是找到一组最合适的weights和biases，使得Loss函数最小，这个过程称为优化，在具体的代码中只需要用已有的优化器即可。

文中作者使用的Loss函数为均方方差损失函数(Mean Squared Loss )，具体表达式为

\[ \begin{align} MSE = MSE_0 &+ MSE_b + MSE_f \tag{1}\\ 其中，\ \ \ \ \ \ \ \ \ &\\ MSE_0 &= \frac{1}{N_0} \sum\limits_{i=1}^{N_0}|h(0,x_0^i)-h_0^i|^2 \tag{2}\\ MSE_b &= \frac{1}{N_b}\sum\limits_{i=1}^{N_b}|h^i(t_b^i,-5)-h^i(t_b^i,5)|^2 + |h_x^i(t_b^i,-5)-h_x^i(t_b^i,5)|^2\tag{3}\\ MSE_f &= \frac{1}{N_f}\sum\limits_{i=1}^{N_f}|f(t_f^i,x_f^i)-0|^2\tag{4} \end{align} \]

下文将MSE记为Loss，\(MSE_0\)记为Loss_0，\(MSE_b\)记为Loss_b，\(MSE_f\)记为Loss_f

算法可以分为两部分，一部分是根据初值条件和边界条件来调整参数，另一部分是根据已知的物理知识，也就是非线性薛定谔方程来进行调整参数。

首先建立神经网络的计算模式，输入层总是x和t，在隐藏层中，每个神经元对上一个神经元的输出H，总是施加\(tanh(w·H+b)\)的操作。最后，我们会得到两个预测值，为什么是两个呢，因为一个是解的实部\(u^i(x,t)\)，一个是解的虚部\(v^i(x,t)\)。上标i表示预测。

说明：\(w\)和\(b\)就是我们希望通过神经网络得到的参数，在实际编程中，将所有神经元对应的\(w\)和\(b\)按照顺序写在矩阵\(weights\)和\(biases\)里。

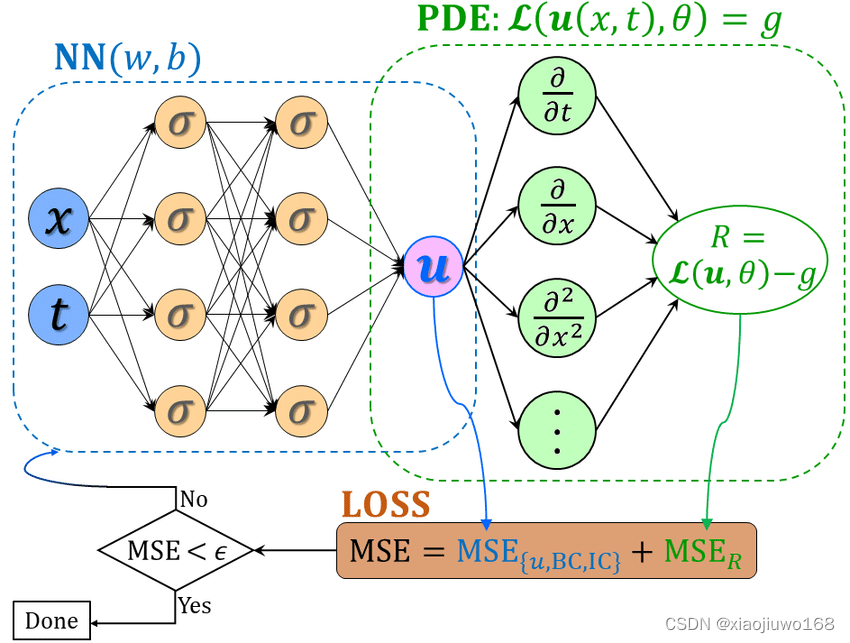
那么我们可以根据初始条件，训练神经网络。初始条件中，t = 0，因此输入x和0。使用神经网络进行一次训练，我们得到了两个预测值\(u^i(x,0)\)和\(v^i(x,0)\)。显然，第一次训练之后得到的解不可能是真实解，于是我们将预测的初始值和真实初始值取均方方差，也就是（2）式，得到Loss_0，以衡量经过一次训练后预测值与真实值的偏离程度。

同理，输入上边界ub和下边界lb，利用周期性边界条件，也就是（3）式，得到 Loss_b .

我们也可以根据（3）式，得到Loss_f 。具体做法是：将在上下界中使用拉丁超立方抽样选取的20000个x以及其一一对应的t作为输入变量，将其输入神经网络后，得到两个输出结果\(u^i(x,t)\)和\(v^i(x,t)\)，将其代入已知的非线性薛定谔方程中，可以. 值得一提的是，将\(u^i(x,t)\)和\(v^i(x,t)\)代入原方程时，需要求导，可以用神经网络的自动微分算法精确求得导数。

最后，Loss = Loss_0+Loss_b+Loss_f .

如果只经历一次训练，我们会发现Loss值是如此的大。于是我们将Loss反向传播回去，希望神经网络可以通过改变weights和biases，使得最终拿到的Loss值越小越好。我们可以设定训练次数，或者收敛情况来决定最终的Loss值小到何种地步。

需要说明的一些技术上的操作：

• 层与层之间使用tanh激活函数。
• 使用xavier方法初始化权重weights和偏置biases。
• 作者使用的优化器有两个，先用Adam优化器预处理，再用L-BFGS-B优化器精细处理。

2.1.1.2 代码实现

if __name__ == "__main__":
    
    noise = 0.0  
	
    # Doman bounds
    lb = np.array([-5.0, 0.0])
    ub = np.array([5.0, np.pi/2])

    N0 = 50  #初始点
    N_b = 50  #边界点
    N_f = 20000  #内部配置点
    layers = [2, 100, 100, 100, 100, 2]
	
    data = scipy.io.loadmat('../Data/NLS.mat')
    t = data['tt'].flatten()[:,None]
    x = data['x'].flatten()[:,None]
    Exact = data['uu']
    Exact_u = np.real(Exact)
    Exact_v = np.imag(Exact)
    Exact_h = np.sqrt(Exact_u**2 + Exact_v**2)

导入数据：

2.1.2 离散时间模型——A-C方程

假设有一个q阶的龙格库塔方程

2.2 \(\lambda\)未知

2.22 连续时间模型