POJ
poj 1995
求表达式(A1B1+A2B2+ ... +AH^BH)mod M.
-
快速幂
-
模运算
与基本四则运算有些相似,但是除法例外。其规则如下:
1.
(a + b) % p = (a % p + b % p) % p (1)
(a – b) % p = (a % p – b % p) % p (2)
(a * b) % p = (a % p * b % p) % p (3)
(a^b) % p = ((a % p)^b) % p (4)
2. 结合律:
((a+b) % p + c) % p = (a + (b+c) % p) % p (5)
((ab) % p * c)% p = (a * (bc) % p) % p (6)
3. 交换律:
(a + b) % p = (b+a) % p (7)
(a * b) % p = (b * a) % p (8)
4. 分配律:
((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p (9)
5. 重要定理:
若a≡b (% p),则对于任意的c,都有(a + c) ≡ (b + c) (%p);(10)
若a≡b (% p),则对于任意的c,都有(a * c) ≡ (b * c) (%p);(11)
若a≡b (% p),c≡d (% p),则 (a + c) ≡ (b + d) (%p),(a – c) ≡ (b – d) (%p),
(a * c) ≡ (b * d) (%p),(a / c) ≡ (b / d) (%p); (12)
代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
ll mod_pow(ll x, ll n, ll mod){
ll res = 1;
while( n > 0 ){
if( n & 1 ) res = res * x % mod;
x = x * x % mod;
n >>= 1;
}
return res;
}
int main() {
int Z, M, H, a, b;
cin >> Z;
while (Z--) {
cin >> M >> H;
ll ans =0;
while (H--) {
cin >> a >> b;
ans += mod_pow(a, b, M);
}
cout << ans % M <<endl;
}
return 0;
}
poj 2092
题意:求第二大的数
计数排序
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <stdlib.h>
using namespace std;
int nCount[10005];
int main()
{
int m, n;
int a;
while(scanf("%d%d", &m, &n) != EOF)
{
if (m == 0 && n == 0)
{
break;
}
int index = 0;
memset(nCount , 0, sizeof(nCount));
for(int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
scanf("%d", &a);
nCount[a]++;
}
}
int max1 = -1, max2 = -1;
for (int i = 1; i <= 10000; i++)
{
if (nCount[i] > max1)
{
max2 = max1;
max1 = nCount[i];
}
else
{
if (nCount[i] > max2)
{
max2 = nCount[i];
}
}
}
int nsum = 0;
for (int i = 1; i <= 10000; i++)
{
if (nCount[i] == max2)
{
if (nsum != 0)
{
printf(" %d", i);
}
else
{
nsum++;
printf("%d", i);
}
}
}
printf("\n");
}
return 0;
}
poj 3061
题意:求连续子序和
尺取法(双指针)
用两个指针,最初都指向这一组数中的第一个,然后如果这个区间的元素之和小于给定的数,就把右指针向右移,直到区间和大于等于给定的值为止。之后把左指针向右移,直到区间和等于给定的值为止,保存方案,继续操作。
复杂度O(n)
①令L=1,先找一下满足要求的第一个长度(当然不一定是最优结果)。期间R++不停伸展。
②满足了是吧,现在踢掉第一个元素,令L++。从第二个元素看起,不符合要求继续伸展R。更新一下ans。继续踢第二个元素。
③踢踢踢,直到不能伸展R,且不符合要求,break。
这种方法只有一个疑问点,就是R不往回移动,其结果一定是对的吗?
考虑一下,L一直向右移动,R其实没必要向左动了。R只有在不满足条件的时候才向右,否则停在原位。
此时凭L的移动已经能找出所有可行的区间了。可以联想一下滑动变阻器,固定R,滑动L。
#include <cstdio>
#include <cstring>
#define INF 0x3f3f3f3f
int main()
{
int T;
int n,s;
int a[100010];
int length;
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&s);
for(int i = 0;i < n;i++)
scanf("%d",&a[i]);
length = INF;
int start = 0;
int end = 0;
int sum = 0;
while(true){
while(end<n && sum<s) sum+=a[end++];
if(sum<s) break;
length = ((end-start)<length)? (end-start): length;
sum-=a[start++];
}
if (length == INF) length = 0;
printf("%d\n", length);
}
return 0;
}
POJ 2785
题意:就是给你4组数,然后让你在每组数里面找一个数,使其4个数和为零。问你有多少组。
题解:可以每两组数相加,和成两个数组,对其中一个数组排序。遍历两个数组(二分法,否则会TE),找相加为零的有多少组。
折半
枚举
##### case1
#include <cstdio>
#include <iostream>
#include <algorithm>
int ab[16000005],cd[16000005];
using namespace std;
int main(){
int n;
scanf("%d",&n);
int a[4000][4];
for(int i = 0; i < n;i++)
scanf("%d%d%d%d",&a[i][0],&a[i][1],&a[i][2],&a[i][3]);
int k1 = 0;
int k2 = 0;
for(int i = 0;i < n;i++)
for(int j = 0;j < n;j++)
{
ab[k1++] = a[i][0] + a[j][1];
cd[k2++] = a[i][2] + a[j][3];
}
sort(cd,cd+k2);
int cnt = 0;
for(int i = 0;i < k1;i++)
{
int left = 0;
int right = k2-1;
int mid;
while(left<=right)
{
mid = (left+right)/2;
if(ab[i] + cd[mid] == 0)
{
cnt++;
for(int j = mid+1;j < k2;j++)
{
if(ab[i] + cd[j] ==0)
{
cnt++;
}
else break;
}
for(int j = mid - 1;j >= 0;j--)
{
if(ab[i] + cd[j] ==0)
{
cnt++;
}
else break;
}
break;//跳出while
}
else if(ab[i] + cd[mid] > 0)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
}
printf("%d",cnt);
return 0;
}
- sort()函数
- 包含在头文件为#include
的c++标准库中; - 有三个参数:
(1)第一个是要排序的数组的起始地址。
(2)第二个是结束的地址(最后一位要排序的地址)
(3)第三个参数是排序的方法,可以是从大到小也可是从小到大,还可以不写第三个参数,此时默认的排序方法是从小到大排序。
sort函数使用模板:
sort(start,end,排序方法)
- 注意二分查找中相等时的操作
case2
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <algorithm>
#include <queue>
#include <iostream>
#include <set>
#include <string.h>
#include <functional>
using namespace std;
int a[4444],b[4444],c[4444],d[4444];
int p [4444 * 4444];
int main()
{
int n ;
while (scanf("%d",&n)!=EOF)
{
for (int i=0;i<n;i++)
scanf ("%d%d%d%d",&a[i],&b[i],&c[i],&d[i]);
for (int i=0;i<n;i++)
for (int j=0;j<n;j++)
{
p[i*n+j] = a[i] + b[j] ;
}
sort (p,p+n*n);
long long ans = 0;
for (int i=0;i<n;i++)
for (int j=0;j<n;j++)
{
int cd = -1*(c[i] + d[j]);
ans += (upper_bound(p,p+n*n ,cd) - lower_bound(p,p+n*n,cd));
}
printf("%I64d\n",ans);
}
return 0;
}
两个二分查找函数:
lower_bound(起始地址,结束地址,要查找的数值) 返回的是数值 第一个 出现的位置。
upper_bound(起始地址,结束地址,要查找的数值) 返回的是数值 最后一个 出现的位置。
POJ 1256
题意:有一个只含大小写字母的字符串,给出所有该字符串的排列,以字典顺序输出。其中 'A'<'a'<'B'<'b'<...<'Z'<'z'。
-
全排列
思路:STL中next_permutation的运用,多写一个比较函数。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
char s[1000];
int cmp(const char& a, const char& b)// 按照'A'<'a'<'B'<'b'<...<'Z'<'z'的顺序,每个字母赋一个固定的权值。
{
int x1 = a;
int x2 = b;
if (x1 >= 'A' && x1 <= 'Z')
x1 = (x1-'A')*2;
else
x1 = (x1-'a')*2+1;
if (x2 >= 'A' && x2 <='Z')
x2 = (x2-'A')*2;
else
x2 = (x2-'a')*2+1;
return x1 < x2;
}
int main()
{
int t;
scanf("%d",&t);
while (t > 0)
{
t--;
scanf("%s",s);
sort(s,s+strlen(s),cmp);
printf("%s\n",s);
while (next_permutation(s,s+strlen(s),cmp))
{
printf("%s\n",s);
}
}
return 0;
}
-
sort()进阶用法
sort(first_pointer,first_pointer+n,cmp)- 使用此函数需先包含:
include
并且导出命名空间:
using namespace std;- 关于cmp:
方法:定义比较函数(最常用)
//情况:数组排列
int A[100];
bool cmp(int a,int b)//int为数组数据类型
{
return a>b;//降序排列
//return a<b;//默认的升序排列
}
sort(A,A+100,cmp);
-
next_permutation()函数
-
函数原型: bool next_permutation(iterator start,iterator end)
当当前序列不存在下一个排列时,函数返回false,否则返回true; -
next_permutation(num,num+n)
对数组num中的前n个元素进行全排列,同时并改变num数组的值。在使用前需要对欲排列数组按升序排序,否则只能找出该序列之后的全排列数
-
next_permutation(node,node+n,cmp)可以对按照自定义的排序方式cmp进行排序。
-
poj 3262
有n头牛,每头牛每分钟会吃D个菜,把这头牛赶回去需要时间T(人再返回又需要T),一次只能赶回去一头牛,也就是说剩下的牛会继续吃菜。求在将所有牛赶回之后。最少吃多少菜
贪心 :按D/T将牛进行排序,然后计算即可
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
struct Cow{
int d,t;
double div;
};
Cow cows[100005];
bool Cmp(const Cow a,const Cow b)
{
return a.div > b.div;
}
int main(){
int n;
scanf("%d",&n);
for(int i = 0;i < n;i++)
{
scanf("%d%d",&cows[i].t,&cows[i].d);
cows[i].div = double(cows[i].d)/double(cows[i].t);
}
sort(cows,cows+n,Cmp);
ll sum = 0;
for(int i = 0;i < n;i++)
sum += cows[i].d;
ll res = 0;
for(int i = 0;i < n;i++)
{
sum -= cows[i].d;
res += cows[i].t * 2 *sum;
}
cout<<res<<endl;
return 0;
}
应注意:
- 采用结构体的形式
- sort()函数的第三个参数的运用
- 最终结果的计算方法
- 最终结果变量应为long long型
POJ 1942
题意:求组合数
- 从n+m个位置,选择n个位放“上” (那么剩下m个位一定是“右”)
codes
#include<iostream>
#include<math.h>
using namespace std;
/*Compute (n+m)C min{n,m}*/
unsigned comp(unsigned n,unsigned m)
{
unsigned a=m+n;
unsigned b=(m<n?m:n);
double cnm=1.0;
while(b>0)
cnm*=(double)(a--)/(double)(b--);
cnm+=0.5; //double转unsigned会强制截断小数,必须先四舍五入
return (unsigned)cnm;
}
int main(void)
{
unsigned m,n;
while(true)
{
cin>>m>>n;
if(!m && !n)//有其中一边为0的矩阵,一定要&&,用||会WA
break;
cout<<comp(n,m)<<endl;
}
return 0;
}
方法:
![]()
- 拆分阶乘,逐项相除,再乘以前面所有项之积。这种方法用一个循环,时间复杂度只有O(n-m)
POJ 2244
约瑟夫问题变形
- N个城市轮流断电,先把城市1断掉,之后便剩下n-1个城市,在这种情况下,求最小的M使胜者为最初的城市2 (换句话说就是现在的城市1)。现在将问题转化一下:在 1...n-1 个数中,求最小的数m,使得胜者为1。
codes
#include <stdio.h>
int main(){
int n,m,i;
int f[1000];
while(scanf("%d",&n) && n)
{
f[1] = 0;
for( m = 2; ;m++)
{
for(i = 2; i < n; i++)
f[i] = (f[i-1] + m) % i;
if(f[n-1] == 0)
{
printf("%d\n",m);
break;
}
}
}
return 0;
}

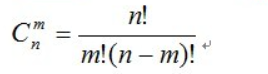


 浙公网安备 33010602011771号
浙公网安备 33010602011771号