基于Matlab的GMSK调制解调代码
免责声明:此为鄙人为了课程设计所作,与行业成熟标准无关,未对信号做足够的分析,可能有很多事实错误和混淆,参考了AI的代码。
代码放最先。
1 % GMSK 调制 2 clc 3 close all; 4 % ============== 1. 参数设置 ============== 5 Fs = 1000e3; % 采样频率 (1MHz) 6 fc = 20e3; % 载波频率 (20 kHz) 7 Rs = 10e3; % 符号速率 (10 kbps) 8 BT = 0.3; % 高斯滤波器带宽-时间积 (典型值 0.3) 9 sps = Fs / Rs; % 每个符号的采样点数 10 data_len = 9; % 比特数目 11 Ts = 1/Rs; % 符号周期 12 t0 = 0:1/Fs:(data_len*Ts)-1/Fs;%计算初始时间轴 13 Snr = 1; %施加高斯白噪声后SNR,如BT较小或者码元数量角度,把值调大 14 15 % ============== 2. 数据准备 ============== 16 data0 = randi([0 1], 1, data_len); % 随机二进制数据 17 %data0 = [0 1 0 1 0 1 1 1 1 0]; 18 %data0 = [1 0 0 0 0 0 1 1 0]; 19 OE_check = mod(data_len,2);%检验数据长度奇偶 20 data_len = data_len + OE_check; 21 data = zeros(1,data_len);%初始化data数组 22 data(1:data_len - OE_check) = data0(1:data_len - OE_check); 23 %如为偶数个码元,则为data(1:data_len) = data0(1:data_len) 24 %如为奇数个码元,就让data为data0后面再补一个0元素,由于data初始化为0数组,无需再操作,省去一个if和一个数组置位 25 %以上方法对偶数很有用,但是对奇数待议 26 27 t = 0:1/Fs:(data_len*Ts)-1/Fs; % 计算补全时间轴 28 len_t = length(t); 29 data_wave0 = reshape(repmat(data0, sps, 1), 1, []);%构造data0波形用于绘图 30 31 % ============== 3. 差分编码 ============== 32 % 使相位变化表示数据 (0->无变化, 1->π/2相位变化) 33 diff_data = zeros(1, data_len);%初始化差分码数组 34 diff_data(1) = data(1); % 初始化第一位 35 for i = 2:data_len 36 diff_data(i) = xor(data(i), diff_data(i-1)); 37 end 38 39 % 映射到双极性信号 (-1 和 +1) 40 bipolar = 2*diff_data - 1; 41 42 % 生成脉冲序列 (NRZ) 43 pulse_train = zeros(1, len_t); 44 for i = 1:data_len 45 idx_start = (i-1)*sps + 1; 46 idx_end = i*sps; 47 pulse_train(idx_start:idx_end) = bipolar(i); 48 end 49 % ============== 4. 高斯滤波 ============== 50 % 计算高斯滤波器参数 51 sigma = sqrt(log(2))/(2*pi*BT); % 高斯滤波器标准差 52 53 % 生成高斯滤波器冲激响应 54 filter_len = 8*sps; % 滤波器长度 (4个符号周期) 55 t_filter = (-filter_len/2 : filter_len/2-1)/Fs; 56 gauss_filter = (sqrt(pi)/sigma)/Ts * exp(-(pi*t_filter/(Ts*sigma)).^2); 57 58 % 归一化滤波器 59 gauss_filter = gauss_filter / sum(gauss_filter); 60 61 % 应用高斯滤波 62 filtered_signal = conv(pulse_train, gauss_filter, 'same'); 63 64 % ============== 5. 串并变换,扩展码元 ============== 65 %I支路对应奇数元素,和sin(Rs*pi*t/2)相乘% 66 %Q支路对应奇数元素,和cos(Rs*pi*t/2)载波相乘% 67 %主要目的为用sin(Rs*pi*t/2)或cos(Rs*pi*t/2)的零点对应抵消各自的跳变处% 68 69 Ik_tx = zeros( 1 , len_t ); 70 for i = 0 : 2 : data_len - 1 - OE_check% Ik 针对奇数个码元优化,且不影响偶数个码元 71 Ik_tx(sps*i + 1:2:sps*(i+2)) = filtered_signal(sps*i + 1:sps*(i+1)); 72 %将高斯滤波后的信号值写到I支路扩展周期的奇数位 73 Ik_tx(sps*i + 2:2:sps*(i+2)) = filtered_signal(sps*i + 1:sps*(i+1)); 74 %将高斯滤波后的信号值写到I支路扩展周期的偶数位 75 end 76 77 % figure; 78 % subplot(3,1,1);plot(t*1e3,filtered_signal); 79 % subplot(3,1,2);plot(t*1e3,Ik_tx); 80 81 Qk_tx = zeros(1,len_t); 82 for i = 1 : 2 : ( data_len - OE_check )%Qk 针对奇数个码元优化,且不影响偶数个码元 83 Qk_tx(sps*(i-1) + 1:2:sps*(i+1)) = filtered_signal(sps*i + 1:sps*(i+1)); 84 %将高斯滤波后的信号值写到Q支路扩展周期的奇数位 85 Qk_tx(sps*(i-1) + 2:2:sps*(i+1)) = filtered_signal(sps*i + 1:sps*(i+1)); 86 %将高斯滤波后的信号值写到Q支路扩展周期的偶数位 87 end 88 % figure; 89 % subplot(3,1,1);plot(t*1e3,filtered_signal); 90 % subplot(3,1,2);plot(t*1e3,Qk_tx); 91 92 %Qk延迟Ts 93 Qk_tx = circshift(Qk_tx,sps);%循环移位1个sps,即1Ts 94 95 %Qk_tx(1:sps)改为与data(1)一致X错误X%改成别的也行吗?,不能随便填写,会出现首个码元出错的情况 96 %当差分码首尾相异填充1,差分码首尾相同填充-1,多次尝试没有首个码元出错,不知道为什么。。。。 97 %是不是和扩频有关系? 98 if xor(bipolar(1),bipolar(length(bipolar)) ) == 1%差分码首尾相异 99 Qk_tx(1:sps) = ones(1,sps); 100 elseif xor(bipolar(1),bipolar(length(bipolar)) ) == 0%差分码首尾相同 101 Qk_tx(1:sps) = -1*ones(1,sps); 102 end 103 104 % % %%采用奇数补齐为偶数的方法,舍去此失败方法,没办法找到规律 105 % % % if mod(length(bipolar),2) == 1 106 % % % if xor(bipolar(1),bipolar(length(bipolar)) ) == 1%差分码末尾两个相异 107 % % % Ik_tx(len_t - sps + 1:len_t) = -1*ones(1,sps); 108 % % % elseif xor(bipolar(1),bipolar(length(bipolar)) ) == 0%差分码末尾两个相同 109 % % % Ik_tx(len_t - sps + 1:len_t) = 1*ones(1,sps); 110 % % % end 111 % % % end 112 113 % ============== 6. MSK调制 ============== 114 % 正交调制 115 I1_tx = Ik_tx .* sin(Rs*pi*t/2); 116 Q1_tx = Qk_tx .* cos(Rs*pi*t/2); 117 118 % 载波调制 119 I2_tx = I1_tx .* sin(2*pi*fc*t); 120 Q2_tx = Q1_tx .* cos(2*pi*fc*t); 121 122 % 两支路相加 123 GMSK_signal = I2_tx + Q2_tx;%按照拟补齐偶数做的 124 GMSK_Tx = zeros(1,(data_len - OE_check) * sps);%初始化最终数组 125 GMSK_Tx( 1:(data_len - OE_check) * sps ) = GMSK_signal(1:(data_len - OE_check) * sps);%如为奇数,则舍去最后一个 126 127 % 调制绘图 128 figure('Position', [0, 100, 1200, 800]); % 设置大窗口 129 130 subplot(6,2,[1,2]); plot(t0*1e3, data_wave0, 'LineWidth', 2); 131 title('原始码(按时间输入)'); 132 xlabel('时间 (ms)'); ylabel('幅度'); 133 subplot(6,2,3); plot(t*1e3,pulse_train, 'LineWidth', 2); 134 title('偶数原始差分码/奇数补齐后差分码'); 135 xlabel('时间 (ms)'); ylabel('幅度'); 136 137 subplot(6,2,4); plot(t*1e3, filtered_signal,'LineWidth', 2); 138 title('高斯滤波后的差分码'); 139 xlabel('时间 (ms)'); ylabel('幅度'); 140 141 subplot(6,2,5); plot(t*1e3, Ik_tx, 'LineWidth', 2); 142 title('Ik_tx (I路)'); 143 xlabel('时间 (ms)'); ylabel('幅度'); 144 subplot(6,2,7); plot(t*1e3, I1_tx); 145 title('I1_tx (I路正交调制后)'); 146 xlabel('时间 (ms)'); ylabel('幅度'); 147 subplot(6,2,9); plot(t*1e3, I2_tx); 148 title('I2_tx (I路载波调制后)'); 149 xlabel('时间 (ms)'); ylabel('幅度'); 150 151 subplot(6,2,6); plot(t*1e3, Qk_tx , 'LineWidth', 2); 152 title('Qk_tx (Q路)'); 153 xlabel('时间 (ms)'); ylabel('幅度'); 154 subplot(6,2,8); plot(t*1e3, Q1_tx); 155 title('Q1_tx (Q路正交调制后)'); 156 xlabel('时间 (ms)'); ylabel('幅度'); 157 subplot(6,2,10); plot(t*1e3, Q2_tx); 158 title('Q2_tx (Q路载波调制后)'); 159 xlabel('时间 (ms)'); ylabel('幅度'); 160 161 subplot(6,2,[11,12]); 162 plot(t0*1e3, GMSK_Tx); 163 title('最终GMSK调制信号'); 164 xlabel('时间 (ms)'); ylabel('幅度'); 165 166 167 %增加高斯白噪声 168 GMSK_with_noise = awgn(GMSK_Tx, Snr, 'measured'); 169 170 %GMSK 解调 171 172 % ============== 1. 正交调制加载波调制 ============== 173 Num_data = length(GMSK_with_noise)/sps; 174 OE_check_rx = mod(Num_data,2); 175 Ik_rx = GMSK_with_noise .* sin(2*pi*fc*t0) .* sin(Rs*pi*t0/2); 176 Qk_rx = GMSK_with_noise .* cos(2*pi*fc*t0) .* cos(Rs*pi*t0/2); 177 Qk_rx = circshift(Qk_rx,-sps);%将Qk_rx向左移位sps位(半个扩展后的码元位) 178 % figure; 179 % plot(Qk_rx); 180 % figure; 181 % plot(Ik_rx); 182 if OE_check_rx == 0%偶数情况处理,无需很多特殊处理 183 Qk_rx_out = zeros(1,Num_data * sps); 184 Ik_rx_out = Ik_rx; 185 Qk_rx_out(1:length(Qk_rx)-sps-1) = Qk_rx(1:length(Qk_rx)-sps-1); 186 Qk_rx_out( length(Qk_rx)-sps + 1 : length(Qk_rx_out) ) = Qk_rx( length(Qk_rx)-sps : -1 :length(Qk_rx)-2*sps + 1 ); 187 %根据观察可知Qk_rx最后为半个扩展后码元位,可以通过倒序填补来补齐 188 %最后需要倒序填补的位置所代表值应为:如前后的各自半个码相同则-1,相异则1,而Qk_rx前半个扩展后码元位总为-1,则末尾补的码元与后半个相同则可 189 %注意 matlab倒序取值的时候,大的值在前面,小的值在后面 190 end 191 192 if OE_check_rx == 1%奇数数情况处理,Ik还处于扩宽码元状态,和上面Qk一样,后面的要多一个sps点会好看点 193 Qk_rx_out = Qk_rx(1 : (Num_data-1) * sps); 194 Ik_rx_out = zeros(1 , (Num_data+1) * sps); 195 Ik_rx_out(1:Num_data * sps) = Ik_rx(1:Num_data * sps); 196 Ik_rx_out( Num_data * sps + 1 : (Num_data + 1) * sps) = Ik_rx( Num_data * sps : -1 : (Num_data-1) * sps + 1); 197 end 198 199 200 % ============== 2. 低通滤波 ============== 201 %通带范围为0-wp,阻带为ws-1的范围 202 wp_l = 1.2*Rs/(Fs/2); %通带截止频率,归一化 203 ws_l = 1.5*Rs/(Fs/2); %阻带截止频率,归一化 204 alpha_pl = 3; %通带允许最大衰减为 db 205 alpha_sl = 40;%阻带允许最小衰减为 db 206 [ N1 , wc1 ] = ellipord( wp_l , ws_l , alpha_pl , alpha_sl);%获取阶数和截止频率 207 [ b_l , a_l ] = ellip(N1,alpha_pl,alpha_sl,wc1,'low');%获得转移函数系数 208 Ik_rx_low = filter(b_l,a_l,Ik_rx_out); %低通滤波 209 Qk_rx_low = filter(b_l,a_l,Qk_rx_out); 210 211 % ============== 3. 判决加并串转换 ============== 212 %没必要先并串转化再判决或者先判决再并串转换,否则又要考虑奇偶问题 213 diff_data_Rx = zeros(1,Num_data);%初始化解调差分码数组 214 for i = 1 : 2 : Num_data - ~OE_check_rx 215 diff_data_Rx(i) = sign(Ik_rx_low(i*sps)); 216 end 217 for i = 2 : 2 : Num_data - OE_check_rx 218 diff_data_Rx(i) = sign(Qk_rx_low(i*sps)); 219 end 220 221 %将双极性码化为单极性码 222 diff_data_Rx = (diff_data_Rx + 1)/2; 223 224 % ============== 4. 解差分编码 ============== 225 data_Rx = zeros(1,Num_data); 226 data_Rx(1) = diff_data_Rx(1); % 初始化 227 for i = 2 : Num_data 228 data_Rx(i) = xor( diff_data_Rx(i-1) , diff_data_Rx(i) ); 229 end 230 231 % disp('原始受调制数据:');disp(data0); 232 % disp('解调后接收数据:');disp(data_Rx); 233 if data0 == data_Rx 234 disp('两者相符,GMSK调制解调成功'); 235 else 236 disp('两者不相符,GMSK调制解调失败'); 237 end 238 239 %解调绘图 240 figure('Position', [50, 50, 1200, 800]); % 设置大窗口 241 242 subplot(5,2,[1,2]); plot(t0*1e3, GMSK_with_noise); 243 title('加白噪声后的GMSK信号'); 244 xlabel('时间 (ms)'); ylabel('幅度'); 245 246 subplot(5,2,3); plot(t(1:length(Ik_rx_out))*1e3,Ik_rx_out); 247 title('混频后Ik_rx (I路)'); 248 xlabel('时间 (ms)'); ylabel('幅度'); 249 subplot(5,2,4); plot(t(1:length(Qk_rx_out))*1e3,Qk_rx_out); 250 title('混频后Qk_rx (Q路)'); 251 xlabel('时间 (ms)'); ylabel('幅度'); 252 253 subplot(5,2,5);plot(t(1:length(Ik_rx_low))*1e3,Ik_rx_low); 254 title('Ik_rx 低通滤波'); 255 xlabel('时间 (ms)'); ylabel('幅度'); 256 subplot(5,2,6);plot(t(1:length(Qk_rx_low))*1e3,Qk_rx_low); 257 title('Qk_rx 低通滤波'); 258 xlabel('时间 (ms)'); ylabel('幅度'); 259 260 diff_data_Rx_wave = reshape(repmat(diff_data_Rx, sps, 1), 1, []);%构造diff_data_Rx波形 261 subplot(5,2,[7,8]);plot(t0*1e3,diff_data_Rx_wave, 'LineWidth', 2); 262 title('解调差分码'); 263 xlabel('时间 (ms)'); ylabel('幅度'); 264 265 data_Rx_wave = reshape(repmat(data_Rx, sps, 1), 1, []);%构造diff_data_Rx波形 266 subplot(5,2,[9,10]); plot(t0*1e3, data_Rx_wave, 'LineWidth', 2); 267 title('GMSK解调信号(按时间输出)'); 268 xlabel('时间 (ms)'); ylabel('幅度');
以下是课设报告。
第一章 仿真综述
GMSK是在MSK的基础上,通过在MSK的串并转换前对上采样的生成的脉冲序列增添一道高斯滤波的调制阶段。因此它能在继承MSK恒包络、相位连续和频谱旁瓣衰减较快的特性下进一步强化频谱旁瓣衰减速度。因此GMSK信号的频谱更为集中,能更好地减少对相邻频道的干扰,更适合密集频谱分配的窄带通信环境,成为GSM等移动通信系统的理想选择。
本次课程设计主要涉及GMSK信号的调制解调,调制解调方案采用的是正交调制解调。主要面临两方面问题:串并转换和考虑奇偶个数码元的处理差异。解决了以上问题后,本次课设的代码可以支持任意正整数个的码元GMSK调制解调。
通过本次课设,发现GMSK信号对白噪声这种幅度上的干扰抵抗能力非常强,但是如果采样率不够高,则在外加高斯白噪声的情况下很容易出现误码。
本次课设使用的主要参数如表1所示。
|
参数名称 |
参数变量名 |
参数量 |
|---|---|---|
|
采样率 |
Fs |
1MHz |
|
载波频率 |
fc |
20kHz |
|
码元速率 |
Rs |
10kHz |
|
码元数量 |
data_len |
任意不太大的正整数 |
|
时宽带宽积 |
BT |
0.3 |
表1
码元数组由代码根据数组随机生成,也可指定data_len长度的二进制数组。
第二章 GMSK调制
2.1 调制简述
GMSK的调制流程如图1所示
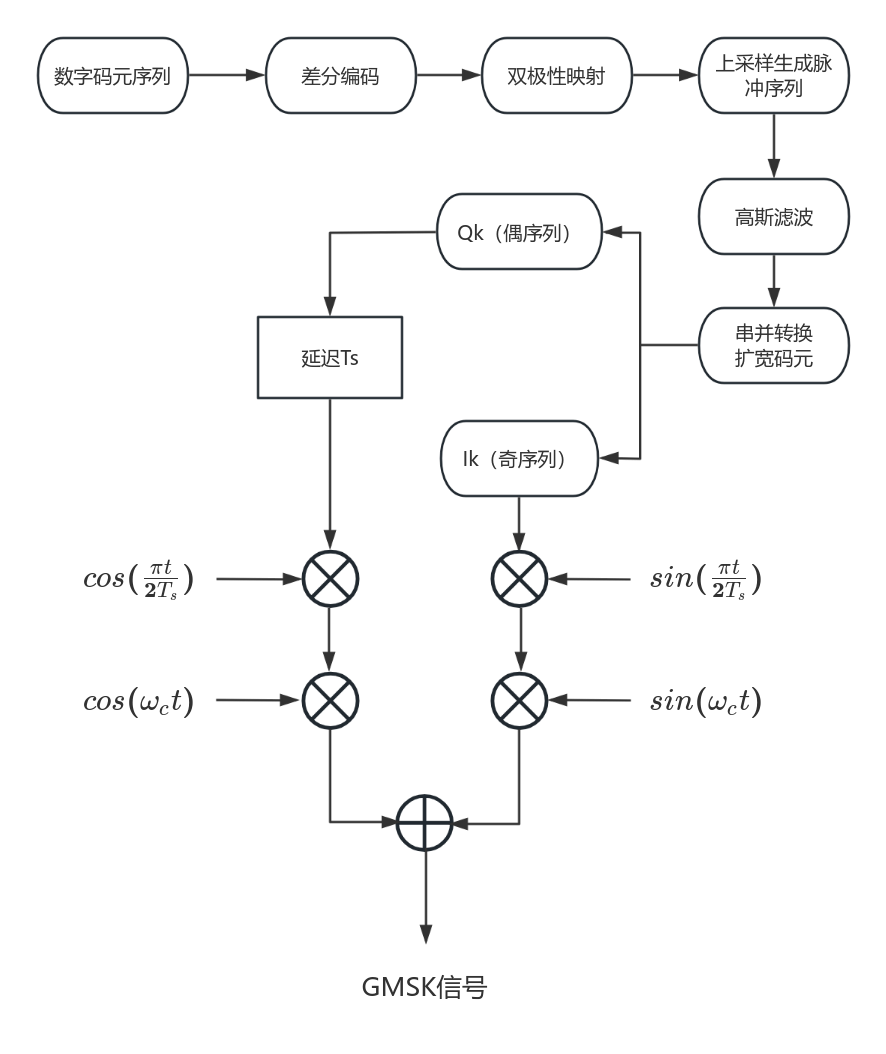
图1
数字码元经过差分编码、双极性映射和上采样后进行高斯滤波,高斯滤波器带宽-时间积BT采用典型值 0.3。在对高斯滤波厚度信号进行串并转换和扩展码元后得到奇序列Ik和延迟Ts后的偶数序列Qk。
分别用余弦波和正弦波与奇偶序列相乘,目的是用正弦波和余弦波的零点去抵消I、Q序列可能的突变点。再分别用载波调制后相加,就得到了GMSK信号。
实现思路:
- 差分编码:差分码首位和原码相同,第i位差分码为第i位原码和第i-1位差分码异或的结果。代码如下:
diff_data(1) = data(1); % 初始化第一位
for i = 2:data_len
diff_data(i) = xor(data(i), diff_data(i-1));
end
- 双极性映射:将差分码各个元素乘2再减去1。代码如下:
bipolar = 2*diff_data - 1;
- 上采样:按照每个码元的长度和采样率,放大到对应的采样数组。先确定单个码元的边界,再整体填入。代码如下:
pulse_train = zeros(1, len_t);
for i = 1:data_len
idx_start = (i-1)*sps + 1;
idx_end = i*sps;
pulse_train(idx_start:idx_end) = bipolar(i);
end
- 高斯滤波:依照高斯函数和给定的时宽带宽积BT来设计高斯滤波器。代码如下:
% 计算高斯滤波器参数
sigma = sqrt(log(2))/(2*pi*BT); % 高斯滤波器标准差
% 生成高斯滤波器冲激响应
filter_len = 4*sps; % 滤波器长度 (4个符号周期)
t_filter = (-filter_len/2 : filter_len/2-1)/Fs;
gauss_filter = (sqrt(pi)/sigma)/Ts * exp(-(pi*t_filter/(Ts*sigma)).^2);
% 归一化滤波器
gauss_filter = gauss_filter / sum(gauss_filter);
% 应用高斯滤波
filtered_signal = conv(pulse_train, gauss_filter, 'same');
高斯滤波后面的串并转换及扩展码元和奇偶序列的处理在本章问题1、2中介绍。正交调制和载波调制以及信号相加合成较为简单,语法上相乘相加即可。
2.2 问题1:串并转换并扩宽码元
GMSK或者说MSK信号如果采用相位积分的形式去做,应当不需要考虑香味问题。但是如果用了串并转换去调制则要明确,串并转换的过程。
串并转换是将原码元上采样后高斯滤波对应的波形按照奇偶进行抽取并且扩宽,得到对应的I、Q序列。此时的IQ序列,每个码元在时域上都是原来的两倍宽而总长度与高斯滤波后的差分码一致。Q序列需要再延迟一个Ts,以确保IQ两路不会同时切换,保证相位不突变。
图2为得到IQ序列后的波形。
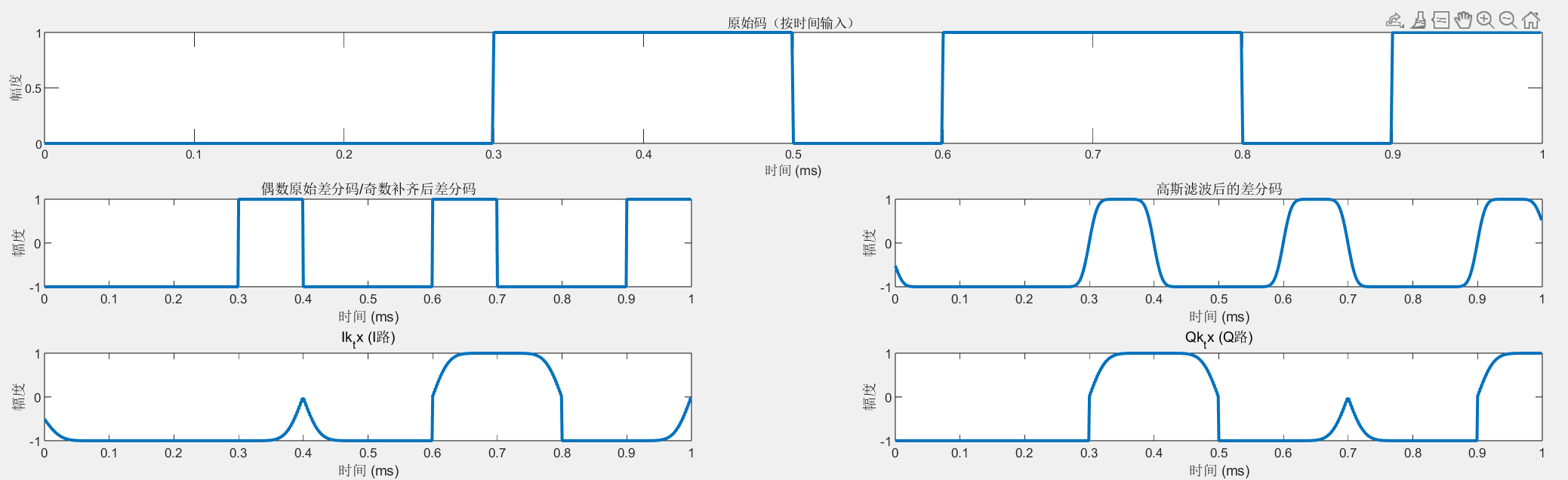
图2
其中扩宽操作采用的是将单个码数组,按照奇偶分别写两遍,尽量避免for循环循环太多次。
处理I支路并无太多麻烦,注意一下data_len的长度确保数组不溢出即可。但是Q支路需要延迟一个Ts,一开始使用循环移位操作,但是最终的调制信号经常出现首个码元错误的情况。由此判断应该是Q支路的前Ts长度出问题,不能用Q支路的最后一个Ts直接移位。如果直接置零首个码会出现幅度问题,直接置为+1或-1仍然会出错。在不断尝试中发现:当差分码首尾相异填充1,差分码首尾相同填充-1。多次尝试没有首个码元出错。
2.3 问题2:奇偶码元问题
在实际的编程、调试过程中,一开始用的是偶数个码元,没考虑奇数个码元的问题。在调制程序基本完成的情况下,尝试奇数个码元经常提示等号左右数组长度不一致。如要实现需要对几乎每个模块进行修改,并且绘图时经常提示数组数目不一致。
在通过互联网搜索和询问AI后,一度想过采用规定码元必须是偶数个的方案。但是考虑将每个奇数个码元数组末尾补0为偶数数组的方案也不改变原有的逻辑并且只要在串并转换和扩宽阶段进行额外的处理,工作量也不会很大。
Matlab的语法糖让选定数组的特定奇偶序列变得比较简单。具体的改变如下:
- 引入data0代替data作为原初码元数组变量,则为data_len在奇数情况下末尾补零,偶数情况下不变的替代数组。具体实现为,通过mod(data0,2)计算奇偶性,初始化data为零数组,长度为data_len + mod(data0,2),再直接将data0赋值给data的前data_len长度,这样无需if语句判断奇偶。代码如下:
OE_check = mod(data_len,2);%检验数据长度奇偶
data_len = data_len + OE_check;
data = zeros(1,data_len);%初始化data数组
data(1:data_len - OE_check) = data0(1:data_len - OE_check);
- 串并转换时额外考虑奇偶不同情况下循环判别码元的次数。循环终止判决代码如下:
for i = 0 : 2 : data_len - 1 - OE_check% Ik 针对奇数个码元优化,且不影响偶数个码元
for i = 1 : 2 : ( data_len - OE_check )%Qk 针对奇数个码元优化,且不影响偶数个码元
GMSK解调
3.1 解调简述
GMSK解调流程如图3所示
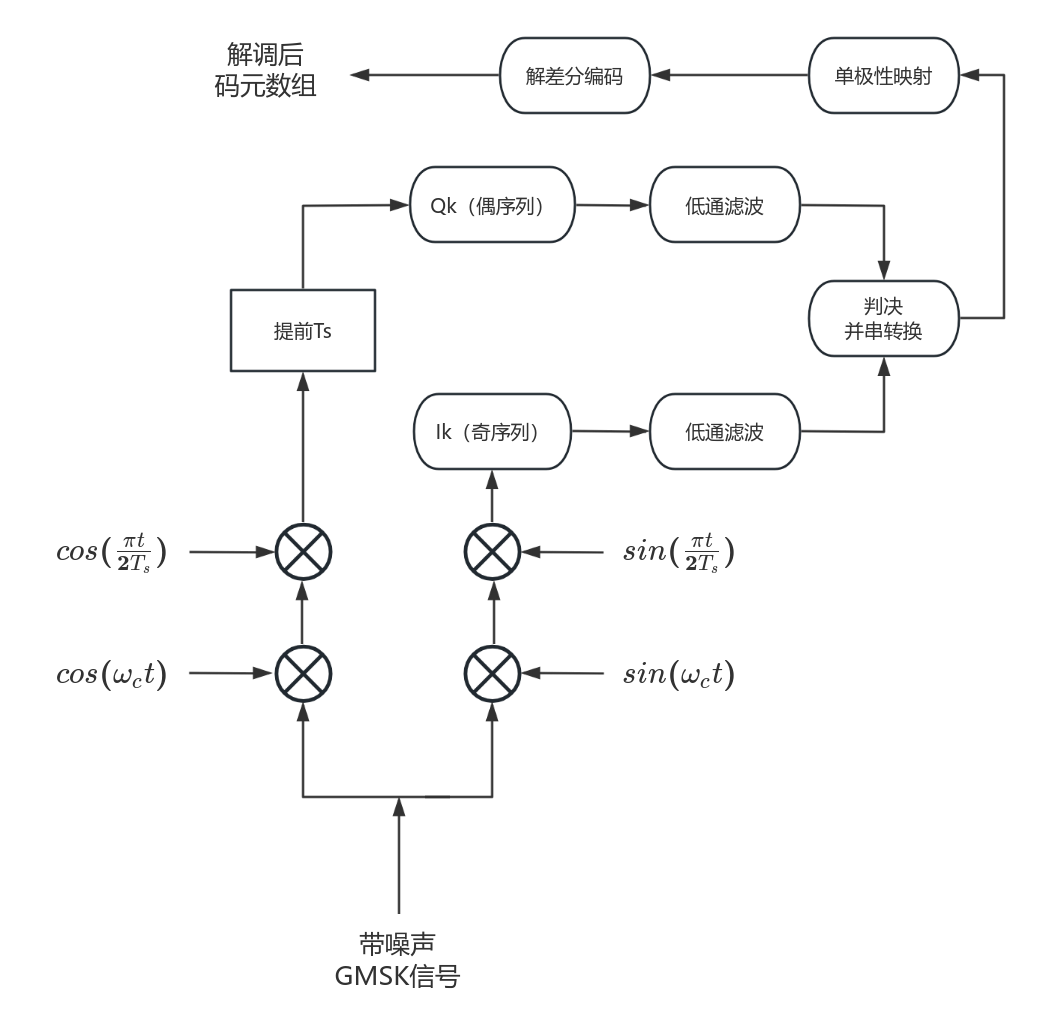
解调过程是调制过程的逆过程,将GMSK信号分别混频后得到两个支路,与余弦信号混频后的Qk支路需要提前Ts。与正弦信号混频后的Ik支路则不需要。混频后两支路的包络已经有明显的幅度信息,对两支路进行低通滤波后即可进行判决。判决后将双极性信号映射为单极性,再经过逆差分编码即可得到解调后的码元数组。
实现思路:
- 混频:由输入的GMSK信号直接与对应波形相乘即可
- 对混频后IQ支路的处理在本章问题1中详述
- 低通滤波:设计好通带阻带参数后利用matlab的ellipord、ellip函数计算阶数、截止频率和转移函数系数,最后应用filter函数处理。代码如下:
%通带范围为0-wp,阻带为ws-1的范围
wp_l = 1.2*Rs/(Fs/2); %通带截止频率,归一化
ws_l = 1.5*Rs/(Fs/2); %阻带截止频率,归一化
alpha_pl = 3; %通带允许最大衰减为 db
alpha_sl = 40;%阻带允许最小衰减为 db
[ N1 , wc1 ] = ellipord( wp_l , ws_l , alpha_pl , alpha_sl);%获取阶数和截止频率
[ b_l , a_l ] = ellip(N1,alpha_pl,alpha_sl,wc1,'low');%获得转移函数系数
Ik_rx_low = filter(b_l,a_l,Ik_rx_out); %低通滤波
Qk_rx_low = filter(b_l,a_l,Qk_rx_out);
- 判决和串并转换:对低通滤波后的信号直接取IQ支路对应的宽码元的中心点对应的幅值,正数取1,负数取-1。代码如下:
diff_data_Rx = zeros(1,Num_data);%初始化解调差分码数组
for i = 1 : 2 : Num_data - ~OE_check_rx
diff_data_Rx(i) = sign(Ik_rx_low(i*sps));
end
for i = 2 : 2 : Num_data - OE_check_rx
diff_data_Rx(i) = sign(Qk_rx_low(i*sps));
end
- 单极映射:将双极性差分码加1后再除以2。代码如下:
diff_data_Rx = (diff_data_Rx + 1)/2;
- 解差分编码:原码第1位等于差分码第1位。原码第i位等于差分码第i位和第i-1位的异或。代码如下:
data_Rx(1) = diff_data_Rx(1); % 初始化
for i = 2 : Num_data
data_Rx(i) = xor( diff_data_Rx(i-1) , diff_data_Rx(i) );
end
3.2 问题1:针对奇偶不同情况在低通滤波前处理信号
1. 判断接收的信号的长度,这里直接用总长度除以码元长度
2. 偶数情况下使Q支路提前一个Ts,这里使用循环移位如下图所示。
移位后末尾的数据需要处理。此处是将最后一个Ts长度补齐为倒数第二个Ts的镜像。代码如下:
if OE_check_rx == 0%偶数情况处理,无需很多特殊处理
Qk_rx_out = zeros(1,Num_data * sps);
Ik_rx_out = Ik_rx;
Qk_rx_out(1:length(Qk_rx)-sps-1) = Qk_rx(1:length(Qk_rx)-sps-1);
Qk_rx_out( length(Qk_rx)-sps + 1 : length(Qk_rx_out) ) = Qk_rx( length(Qk_rx)-sps : -1 :length(Qk_rx)-2*sps + 1 );
%根据观察可知Qk_rx最后为半个扩展后码元位,可以通过倒序填补来补齐
end
- 奇数情况下Q支路不需要额外处理,只要把循环左移Ts后最后一个Ts的数据去掉。I支路如下图所示,最后一个码元只有一般的宽度(1个Ts)。

为了装下所有的扩展之后的码元方便后面判决的统一处理,应当扩展一个Ts。这个Ts是镜像前一个Ts,采用前一个Ts的倒序排列即可。
if OE_check_rx == 1%奇数数情况处理,Ik还处于扩宽码元状态,和上面Qk一样,后面的要多一个sps点会好看点
Qk_rx_out = Qk_rx(1 : (Num_data-1) * sps);
Ik_rx_out = zeros(1 , (Num_data+1) * sps);
Ik_rx_out(1:Num_data * sps) = Ik_rx(1:Num_data * sps);
Ik_rx_out( Num_data * sps + 1 : (Num_data + 1) * sps) = Ik_rx( Num_data * sps : -1 : (Num_data-1) * sps + 1);
End
4.2 十个码元 0 1 0 1 0 1 1 1 1 0
0 1 0 1 0 1 1 1 1 0 调制过程:
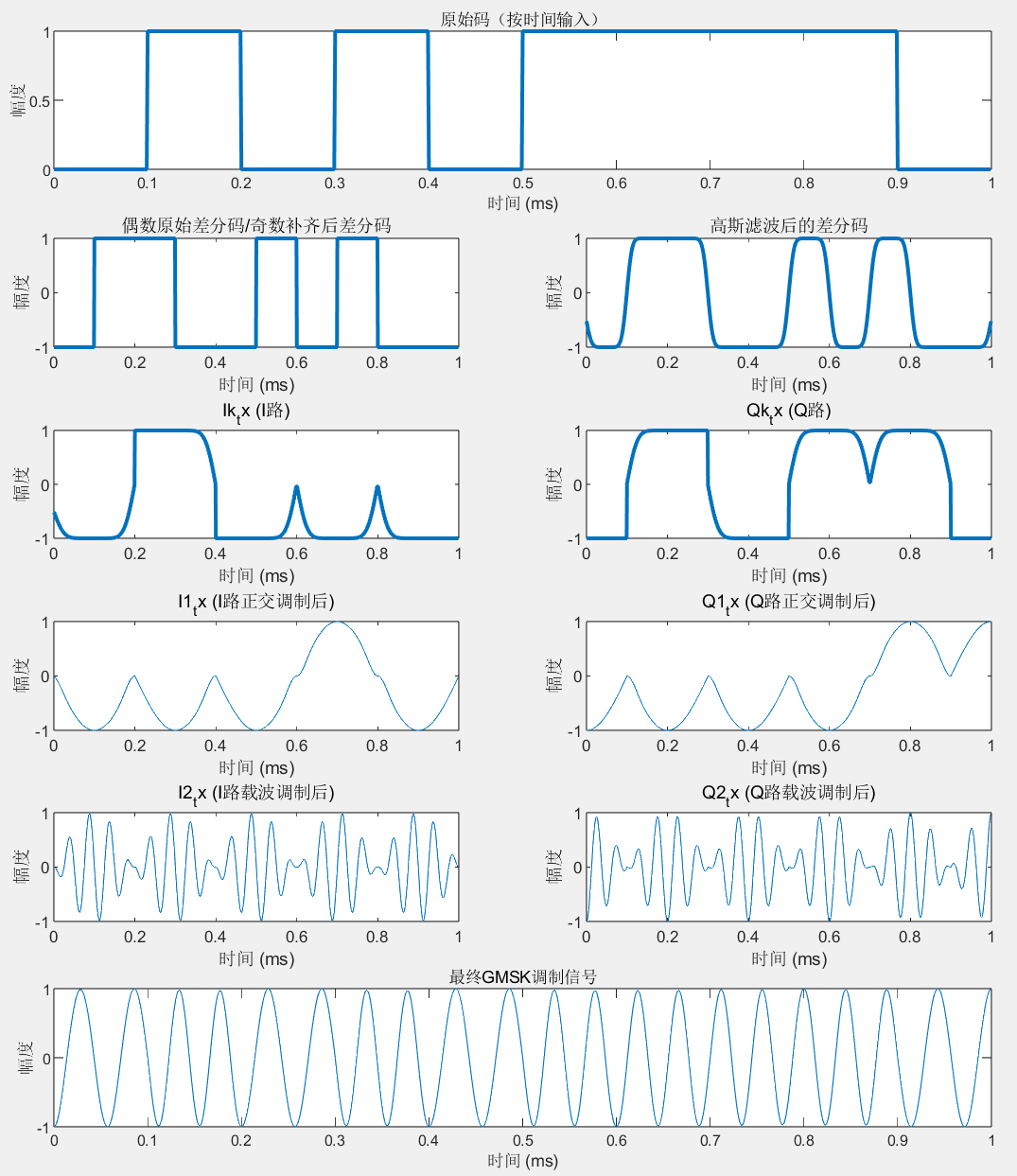
0 1 0 1 0 1 1 1 1 0 解调过程:
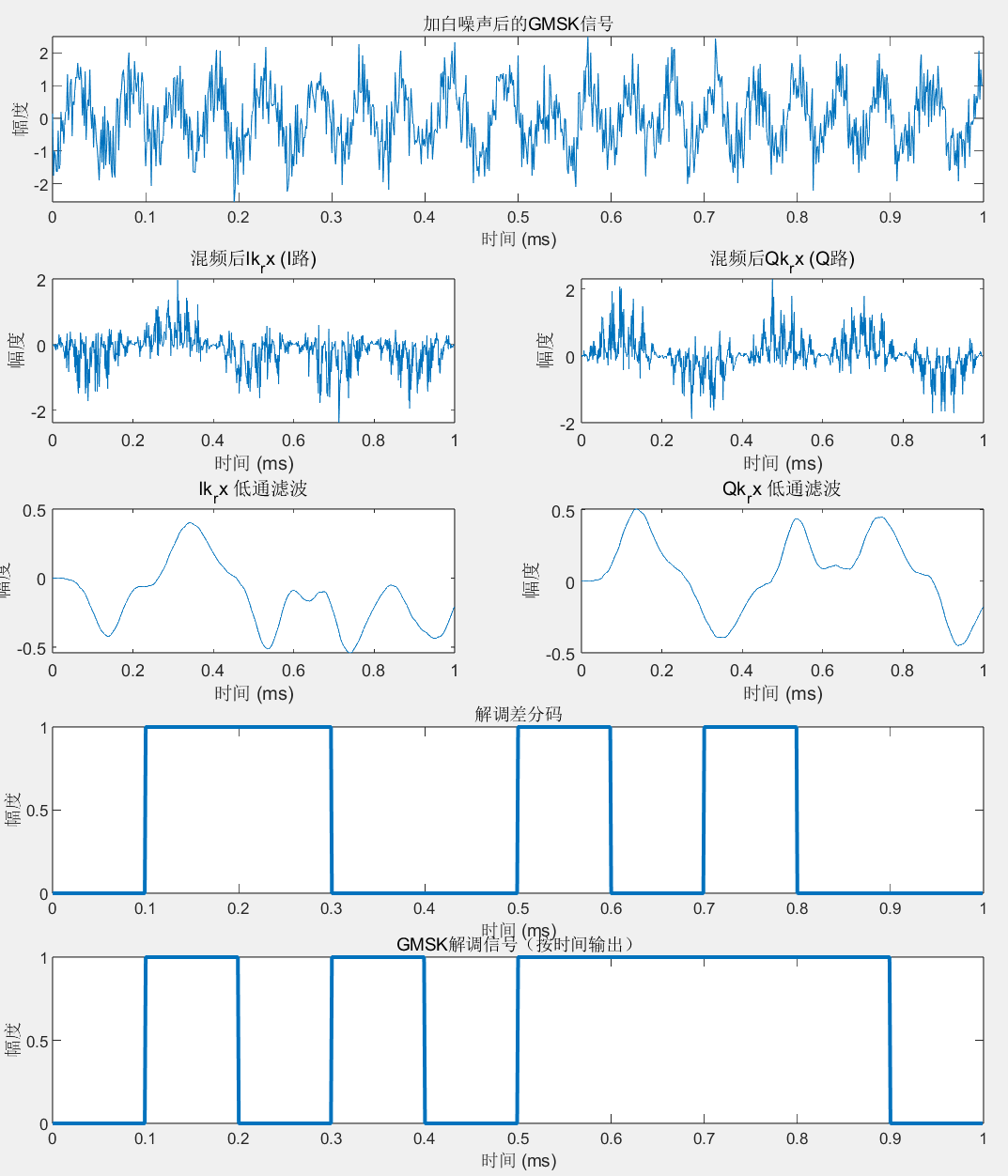


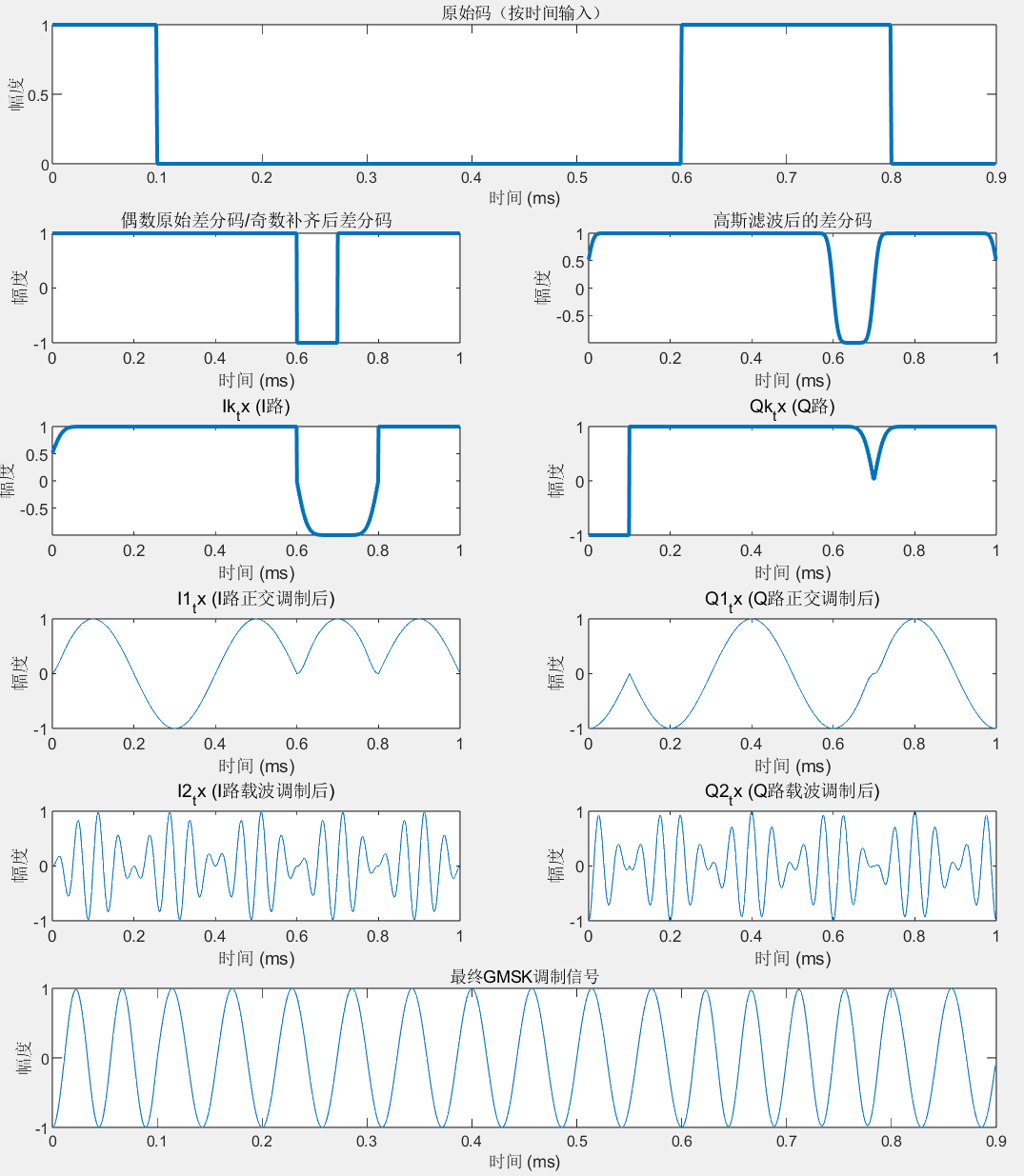
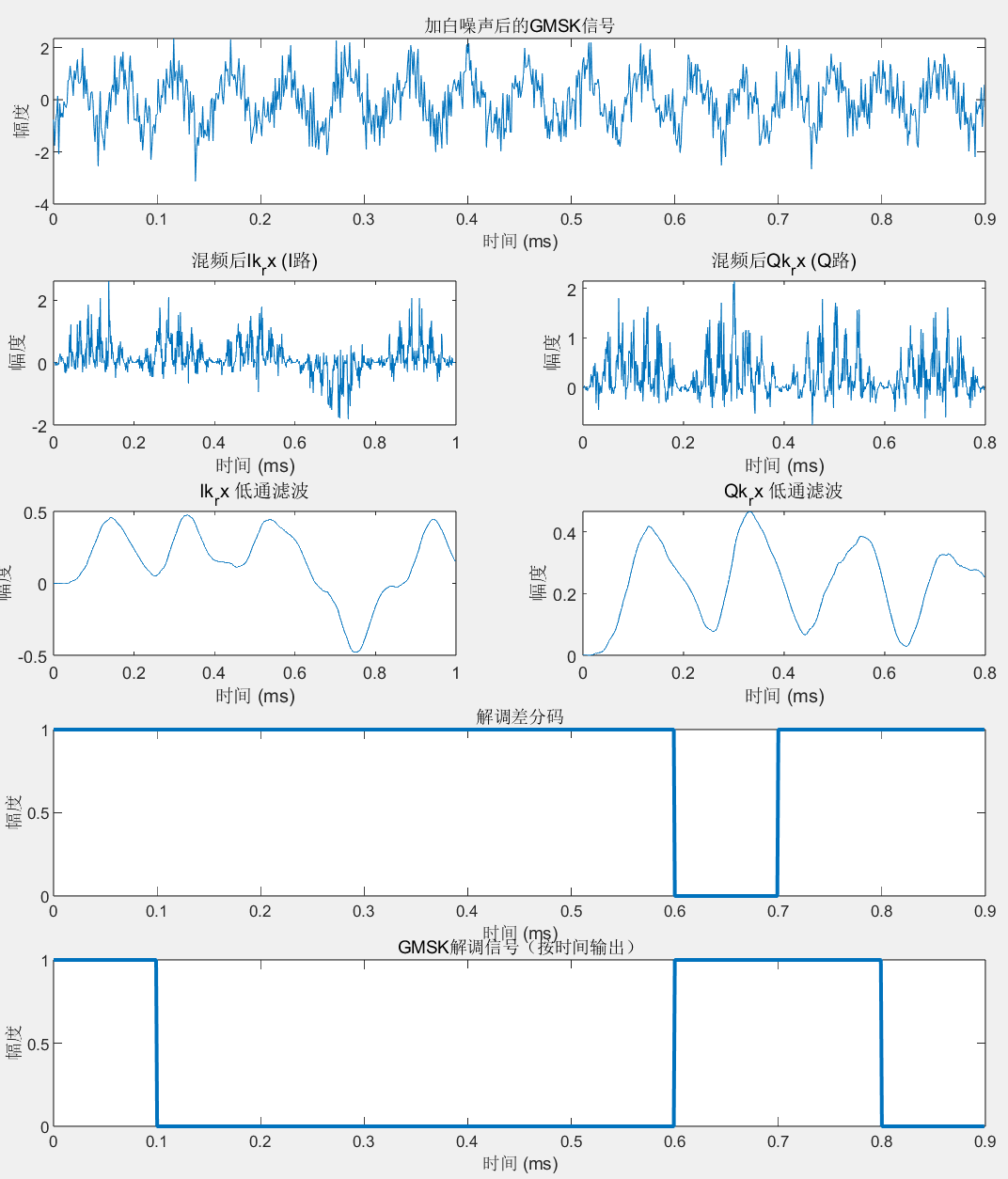

 浙公网安备 33010602011771号
浙公网安备 33010602011771号