Tarjan求LCA
前言:
没想到吧,\(tarjan\)不仅可以用来求割点和桥,缩点,还能求\(LCA\)。不过,\(tarjan\)求\(LCA\)是离线的,要在线算法的话还是学倍增吧。
正题:
这次的\(tarjan\)不需要回溯值和\(dfs\)序,本质的来说,其实\(tarjan\)求\(LCA\)跟割点和桥,缩点没有任何关系一个人发明的算不算。
前置知识:并查集
当然,\(tarjan\)的其他两个算法跟\(dfs\)有关,求\(LCA\)也不例外,我们是在\(dfs\)的基础上,一步一步求出来的。
步骤如下:
-
对这课树进行\(dfs\),从根开始
-
对于每个节点,我们不先标记这个点走过,回溯的时候才标记
-
对于每个节点,遍历与之相邻且未走过的点,并把这些点的父亲标记为当前节点,相当于合并这些点
-
对于每个节点,当与之相邻的点遍历完后,查询在求LCA问题中与自己相关的问题,看它问题中的另外一个点有没有被查询到,有的话就把这两个点的答案赋值为另外一个点的父亲(当然是合并后的父亲)
第三步的是否走过时指遍历到了没有,不是标记。对于合并,合并后查询父亲,我们就用并查集来完成。
这样自然是不好理解的,来看个例子(以下的\(find\)函数就是普通并查集的\(find\)):

这是我们的图,现在假设我们要求\(3\)和\(4\),\(2\)和\(6\)的\(LCA\)。
先进行第一步,此时我们先是从\(1\)开始搜,先到的地方是\(3\),然后看与\(3\)相关的节点\(4\),\(4\)没有被搜到,我们就退出,并标记\(3\),把他的父亲标记为\(2\),合并掉\(3\)。
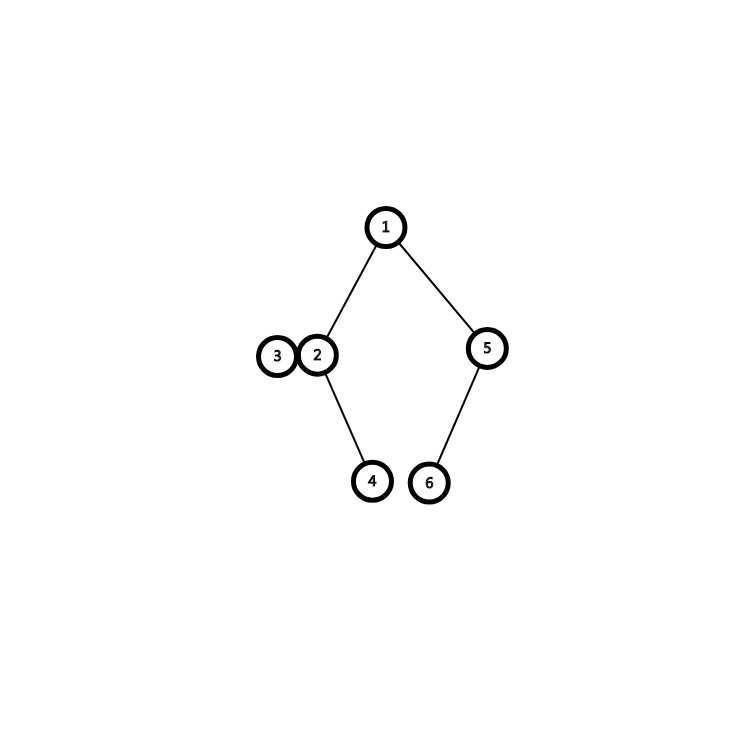
此时,\(2\)的儿子没遍历完开始遍历\(4\),与\(4\)相关的节点\(3\),是搜过的,此时\(LCA\)\(3\),\(4\)就是\(find\)(\(3\))也就是\(2\)(注意不能\(find\)(\(4\)),而是\(find\)与之相关的另外一个节点)。然后合并\(4\),把\(4\)的父亲标记为\(2\)。
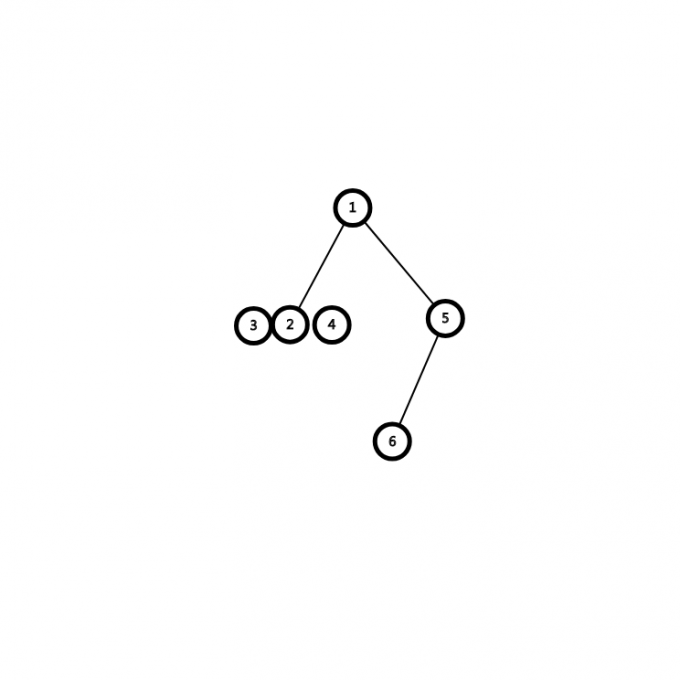
这时应该遍历\(2\)了,发现与之相关的\(6\)未找到,于是把\(2\)的父亲标记为\(1\),自然,此时\(3\),\(4\)的父亲也为\(1\)了。

后面的就以此类推了。这一步应该判断\(6\),求出\(LCA2\),\(6\)为\(1\),合并\(6\),标记父亲。
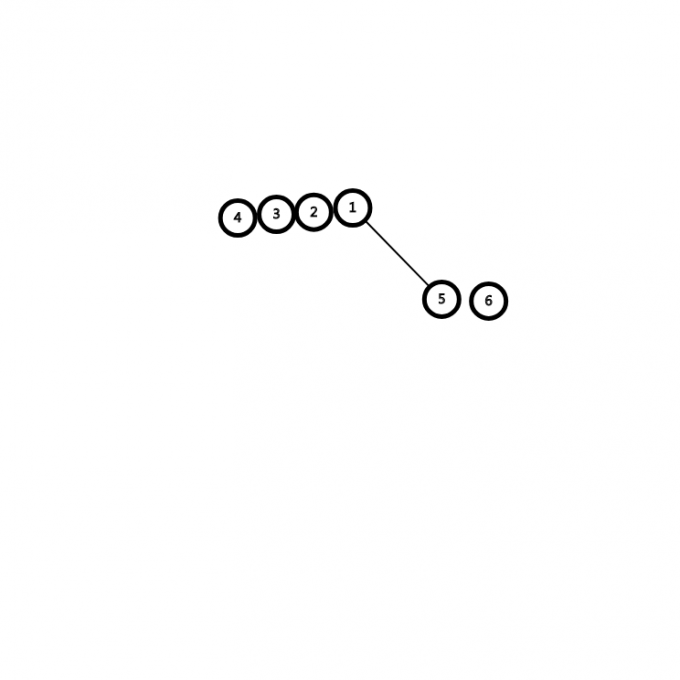
把\(5\)合并,父亲为\(1\)。
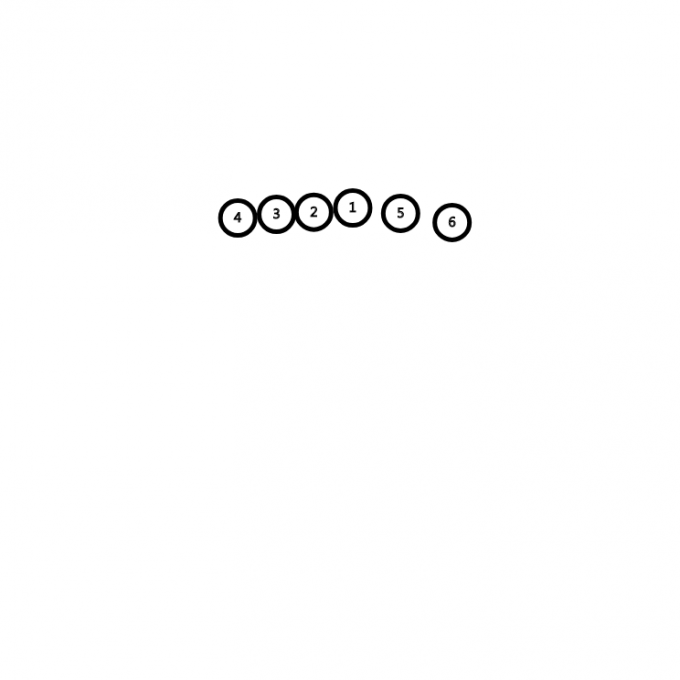
到\(1\)了后就没有了,算法完结。
接下来讲讲实现。
例题:
这就是模板了吧,我把代码贴一贴,理解一下(特别短!!!而且这道题对于倍增和\(RMQ\)都需要卡卡常,而\(tarjan\)我用\(vector\)建图不加快读快写就能过,当然得把注释删掉,不然会\(T\))。
代码:
#include <bits/stdc++.h>
using namespace std;
struct node{
int p , id;
}; //代表与之相关的点和这一对LCA是第几个答案
int n , m , root;
int fa[500010] , vis[500010]/*标记+判断是否走过*/ , ans[500010];
vector<int> e[500010]; //建边
vector<node> q[500010]; //存储问题
int find(int x){ //路径压缩
if(fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
void tarjan(int x){
vis[x] = 2; //2表示走过
for(int i = 0; i < e[x].size(); i++){
int nx = e[x][i];
if(vis[nx]) continue;
tarjan(nx);
fa[nx] = x; //标记父亲
}
for(int i = 0; i < q[x].size(); i++){
int px = q[x][i].p , ix = q[x][i].id; //找与之相关的点
if(vis[px] == 1) ans[ix] = find(px);
}
vis[x] = 1; //1表示标记过
}
int main(){
cin >> n >> m >> root;
for(int i = 1; i <= n; i++) fa[i] = i; //并查集初始化
for(int i = 1; i <= n - 1; i++){
int x , y;
cin >> x >> y; //建图,注意双向边(被坑过)
e[x].push_back(y);
e[y].push_back(x);
}
for(int i = 1; i <= m; i++){
int x , y;
cin >> x >> y; //因为我们在tarjan过程中不知道求的是第几个答案,所以要存储一下这一对LCA是第几个答案
q[x].push_back((node){y/*与之相关的点*/ , i/*第几个答案*/});
q[y].push_back((node){x , i});
}
tarjan(root); //跑LCA
for(int i = 1; i <= m; i++) cout << ans[i] << endl; //输出
return 0;
}
再来一道例题:
这道题还需要用到最小生成树。
先讲下思路吧。
对于一些道路,我们在保证图的连通性时,是可以删掉的,就如样例的边\(1\),\(3\),我们是肯定不会走这条路的,题目没有要求路更短,那么我们就可以删掉一些小边,只要不破坏图的连通性就行(原来就不连通那可没办法了),这时,我们可以想到最大生成树,把小边删掉,保留大边,这样就可以既保证图的连通性,又减少冗余的边。接下来,对于一棵树,任意两点是不是就只有一条路径了,我们就可以求出要求的两点的\(LCA\),然后从两个点往上查找,直到找到他们的\(LCA\),取最小值,最后输出即可。
当然,可以优化的,具体应该是在\(tarjan\)过程中就求出他们的路径和最小值,但是我太菜了死活没想出来,只能想到这里了。
代码:
#include <bits/stdc++.h>
using namespace std;
struct node{
int l , r , w;
}; //存边
node ed[300010];
int n , m , q , now;
int fa[300010] , vis[300010] , lca[300010] , rf[300010]/*存往上走的路径*/ , wrf[300010]/*存LCA往上走时的边权*/ , qu1[300010] , qu2[300010]/*存问题的节点*/;
vector<pair<int , int> > e[300010]; //跑完最大生成树后再建边
vector<pair<int , int> > ques[300010]; //存问题
int find(int x){
if(fa[x] == x) return x;
return fa[x] = find(fa[x]);
}
bool cmp(node x , node y){ //最大生成树
return x.w > y.w;
}
void trajan(int x){
vis[x] = 2; //走过
for(int i = 0; i < e[x].size(); i++){
int nx = e[x][i].first;
if(vis[nx]) continue;
trajan(nx);
rf[nx] = x; //存往上走的路径
wrf[nx] = e[x][i].second; //存路径值
fa[nx] = x;
}
for(int i = 0; i < ques[x].size(); i++) //存LCA
if(vis[ques[x][i].first] == 1) lca[ques[x][i].second] = find(ques[x][i].first);
vis[x] = 1; //标记走过
}
int dfs(int x , int need){ //找路径最小值
if(x == need) return 0x3fffff; //为本身
if(rf[x] == need) return wrf[x]; //父亲是LCA就停止
return min(wrf[x] , dfs(rf[x] , need)); //取min
}
int main(){
cin >> n >> m;
for(int i = 1; i <= m; i++) cin >> ed[i].l >> ed[i].r >> ed[i].w;
for(int i = 1; i <= n; i++) fa[i] = i; //最大生成树并查集初始化
sort(ed + 1 , ed + m + 1 , cmp);
for(int i = 1; i <= m; i++){
int fx = find(ed[i].l) , fy = find(ed[i].r);
if(fx == fy) continue;
fa[fx] = fy;
e[ed[i].l].push_back(make_pair(ed[i].r , ed[i].w)); //建图
e[ed[i].r].push_back(make_pair(ed[i].l , ed[i].w));
now++;
if(now == n - 1) break;
}
cin >> q;
for(int i = 1; i <= n; i++) fa[i] = i;
for(int i = 1; i <= q; i++){
int x , y;
cin >> x >> y;
qu1[i] = x , qu2[i] = y;
ques[x].push_back(make_pair(y , i)); //存问题
ques[y].push_back(make_pair(x , i));
}
for(int i = 1; i <= n; i++)
if(!vis[i]) trajan(i);
for(int i = 1; i <= q; i++){
if(find(qu1[i]) != find(qu2[i])){ //不是同一个联通快
cout << -1 << endl;
continue;
}
int min1 = dfs(qu1[i] , lca[i]) , min2 = dfs(qu2[i] , lca[i]);
if(qu1[i] == qu2[i]) cout << 0 << endl; //如果两个相等
else cout << min(min1 , min2) << endl; //取min
}
return 0;
}
废话结束,正片开始,学\(Treap\)去了,把以前坑填了



 浙公网安备 33010602011771号
浙公网安备 33010602011771号