数据结构
数据结构
定义
数据结构就是设计数据以何种方式组织并存放在计算机中
eg:列表,字典,元组,堆,栈,队列
程序 = 数据结构(静态的数据) + 算法(动态的操作)
分类
- 逻辑结构
- 线性(一对一)
- 非线性
- 树结构(一对多)
- 图结构(多对多)
- 集合结构(除属于同一集合,别无其它关系)
- 存储结构(物理结构)
- 顺序存储结构(列表)
- 链式存储结构
注:逻辑上为非线性结构,存储结构可以以线性结构存储,eg:堆(在逻辑上试属于非线性结构中的树,但可以以线性存储结构中的列表存储)
c语言数组与python中列表的区别
- c语言需设置存储空间大小
- 两者空间存储内容范围不同
![image]()
c语言数组只能存储同一类型元素,python可存储不同类型元素,由于python不同类型元素所占的字节不同,无法定义数组容量,因此,python数组存储元素的地址,占用一片连续的空间。
插入删除的时间复杂度为:O(n)
栈
特点
后进先出(last in first out:LIFO)
基本操作
- 进栈:push
- 出栈:pop
- 取栈顶(不拿走):gettop
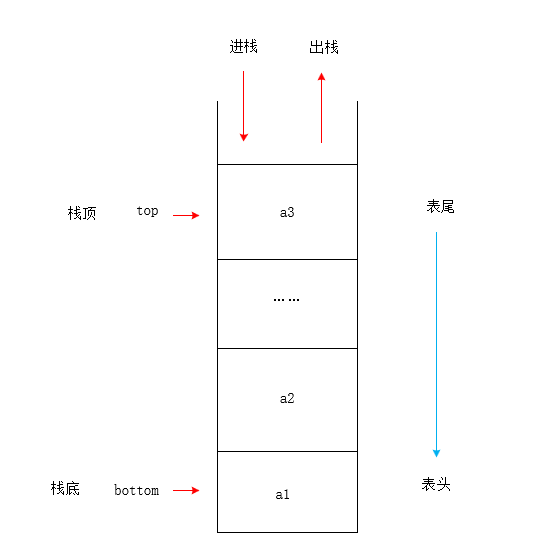
栈的实现
- 进栈:li.append
- 出栈:li.pop
- 取栈顶:li[len(li)-1]
# 栈
# 访问该类属性格式:self+.+属性
class Stack: # 定义一个栈类
def __init__(self): # 初始化栈
self.stack = []
def push(self,element): # 进栈方法
self.stack.append(element)
def pop(self): # 出栈方法
if len(self.stack) > 0: # 判断栈类是否有元素
return self.stack.pop()
else:
return None
def get_top(self): # 获取栈顶元素方法
if len(self.stack) > 0: # 判断是否存在栈顶元素
return self.stack[-1]
else:
return None
stack = Stack()
stack.push(9)
stack.push(6)
stack.push(6)
print(stack.pop())
print(stack.pop())
print(stack.get_top())
栈的应用
# 栈的括号匹配问题
class Stack:
def __init__(self):
self.stack = []
def push(self,element):
self.stack.append(element)
def pop(self):
if len(self.stack) > 0:
return self.stack.pop()
else:
return None
def get_top(self):
if len(self.stack) > 0:
return self.stack[-1]
else:
return None
def is_empty(self):
return len(self.stack) == 0
def brace_match(s):
stack = Stack()
catch = {"]":"[","}":"{",")":"("}
for i in s:
if i in "([{":
stack.push(i)
else:
if stack.is_empty():
stack.push(i)
elif catch[i] == stack.get_top():
stack.pop()
else:
stack.push(i)
if stack.is_empty():
print("匹配")
else:
print("不匹配")
str = str(input())
brace_match(str)
队列
特点
先进先出(first in first out:FIFO)
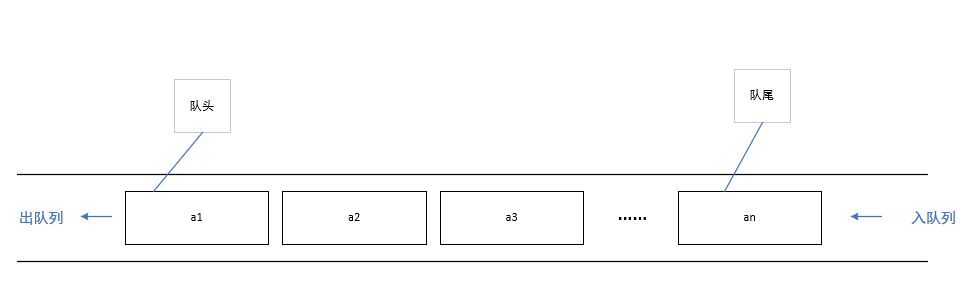
队列的实现——环形队列
原理
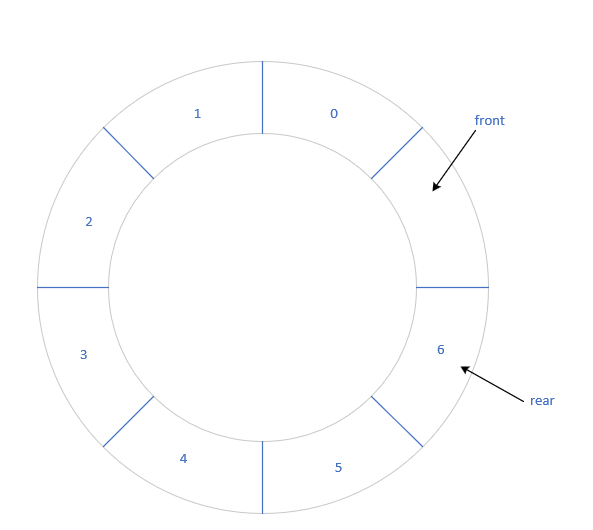
队首指针往下一格:(front+1)%MaxSize
队尾指针往下一格:(rear+1)%MaxSize
队满条件:(rear+1)%MaxSize == front
队空条件:font == rear
实现
# 堆的底层实现
class Queue:
def __init__(self,size): # 指定列表空间大小
self.size = size
self.queue = [0 for _ in range(size)]
self.rear = 0 # rear表示队尾元素
self.front = 0 # front表示队头元素
def push(self,element):
if not self.is_filled():
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = element
else:
raise Exception("队满了!")
def pop(self):
if not self.is_empty():
self.front = (self.front + 1) % self.size
return self.queue[self.front]
else:
raise Exception("队空了!")
# 队空情况
def is_empty(self):
return self.rear == self.front
# 队满情况
def is_filled(self):
return (self.rear + 1) % self.size == self.front
queue = Queue(7)
for i in range(6):
queue.push(i)
print(queue.pop())
双端队列
同时具有队列和栈的特点:元素可以从两端进行删除和插入操作
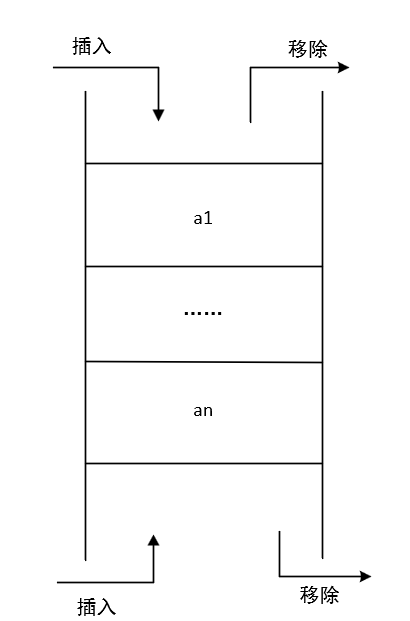
python队列内置模块的实现
from collections import deque
# 单向队列
queue = deque()
for j in range(10):
queue.append(j) # 在队尾插入元素
print(queue.popleft()) # 在队首移除元素
# 多向队列
for i in range(20,30):
queue.appendleft(i) # 在队首插入元素
print(queue.pop()) # 在队尾移除元素
队列的应用
# 队列的应用(从文件中读取后n行)
from collections import deque
def tail(n):
with open(r"C:\Users\hby\Desktop\1.txt","r") as f:
queue = deque(f,n)
# f表示初始化一个队列,n表示队列所能存放的最大空间,若超过,dequeue会将前面的元素移除,最后保留后加入的n给元素
return queue
for i in tail(5):
print(i,end="")
栈和队列的应用
背景
迷宫问题:给一个二维列表,表示迷宫(0表示通道,1表示围墙)。给出算法,求一条走出迷宫的路径。
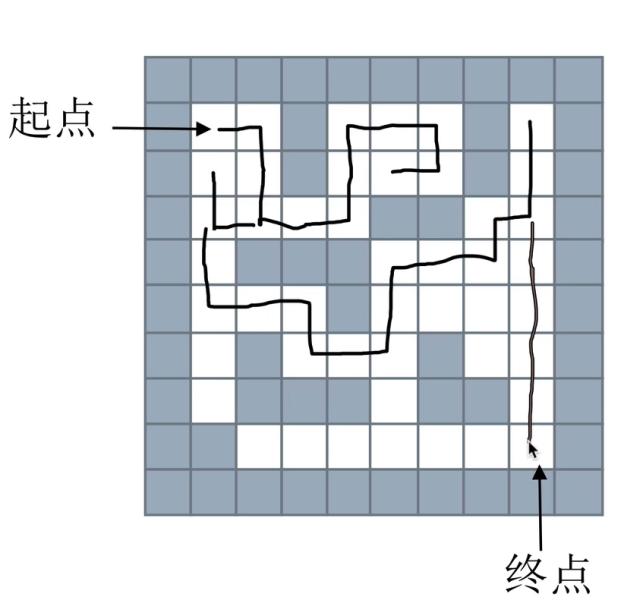
栈(深度优先搜索:一条路走到黑)
回溯法
- 原理:通过一定法则,进行搜索,并将路径保存在栈内存中,当元素走到头时,将该元素出栈,找到栈内还有可走路径的元素为止,停止出栈,最后到终点,则该栈中的元素则为到达终点的一条路径(并不一定是最短路径)
- 实现
# 迷宫
maze = [
[1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
direction = [ # 用于存储给出参数为(x,y)的上下左右坐标位置
lambda x,y:(x+1,y),
lambda x,y:(x,y+1),
lambda x,y:(x-1,y),
lambda x,y:(x,y-1)
]
def path(x1,y1,x2,y2): # x1,y1表示起始点;x2,y2表示终点
stuck = [] # 将路径点存放在列表(可进行增加和删除操作)stuck中
stuck.append((x1,y1))
while(len(stuck)>0): # 当列表还存在元素时(表示可能还有通路)
curNode = stuck[-1] # 记录已走到最末的当前点位置
if curNode == (x2,y2): # 当走到终点时,输出终点
for i in stuck:
print(i)
return True
for i in direction:
newNode = i(curNode[0],curNode[1]) # 找到末点的后面的点位置,得到一个坐标(x,y)
if maze[newNode[0]][newNode[1]] == 0: # 判断该点是否是通路
stuck.append(newNode) # 是通路则存放列表中
maze[newNode[0]][newNode[1]] = 2 # 改变该点的标志为2,说明该点已走过
break # 以新的点进行重新while循环,进行深度优先搜索
else:
# 若当前点都没有下一个可走位置,则去除该点,找到前一个点,如此循环,直到找到有可走路径的点为止
stuck.pop()
maze[newNode[0]][newNode[1]] = 2 # 并设该点为已走过的点
else: # 若列表内元素为空,则表明无通路
print("无通路!")
return False
path(1,1,8,8)
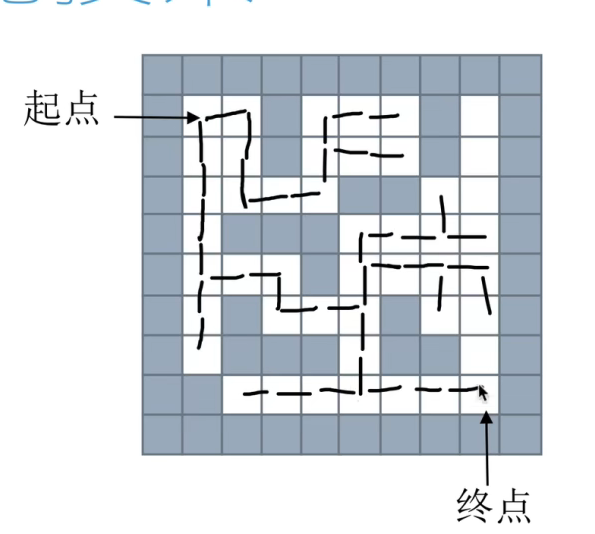
队列(广度优先搜索)
- 原理:考虑一个位置所有可走的位置,分叉多条路,最后得到的路径一定是最短路径,需要一个额外的数组来存储当前位置的源头下标。
- 实现
# 迷宫
maze = [
[1,1,1,1,1,1,1,1,1,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,1,0,0,0,1,0,1],
[1,0,0,0,0,1,1,0,0,1],
[1,0,1,1,1,0,0,0,0,1],
[1,0,0,0,1,0,0,0,0,1],
[1,0,1,0,0,0,1,0,0,1],
[1,0,1,1,1,0,1,1,0,1],
[1,1,0,0,0,0,0,0,0,1],
[1,1,1,1,1,1,1,1,1,1]
]
# 方向
directions = [
lambda x,y:(x+1,y),
lambda x,y:(x,y+1),
lambda x,y:(x-1,y),
lambda x,y:(x,y-1)
]
# 寻回队列前的元素
def maze_back(path):
Node = path[-1] # 从终点开始往回找
realPath = [] # 存放正确的路径
while Node[2] != -1: # 等于-1时即为起始点
realPath.append(Node[0:2])
Node = path[Node[2]]
path.append(Node[0:2])
realPath.reverse() # reverse能够使得列表本身发生颠倒
for i in realPath:
print(i)
# 广度优先搜索
from collections import deque # python内置队列
def maze_path_queue(x1,y1,x2,y2):
queue = deque()
path = [] # 存放移除队列的元素
queue.append((x1,y1,-1)) # -1表示该元素在path里源头的下标
while len(queue) > 0: # 判断找到终点元素前队列是否为空
curNode = queue.pop()
path.append(curNode) # 保存元素,以便后面从终点找起点
if curNode[0] == x2 and curNode[1] == y2:
maze_back(path)
return True
for i in directions:
newNode = i(curNode[0],curNode[1])
if maze[newNode[0]][newNode[1]] == 0:
queue.append((newNode[0],newNode[1],len(path)-1))
maze[newNode[0]][newNode[1]] = 2
else:
print("无通路!")
return False
maze_path_queue(1,1,8,8)
链表
定义
由一系列结点组成的元素集合
包含两部分:数据域(item)& 指针域(next)
数据域:存放数据
指针域:存放下一个结点的地址,指向下一个结点的位置
结点与结点之间不是顺序存放,结点内部之间则是顺序存放
链表的创建和遍历
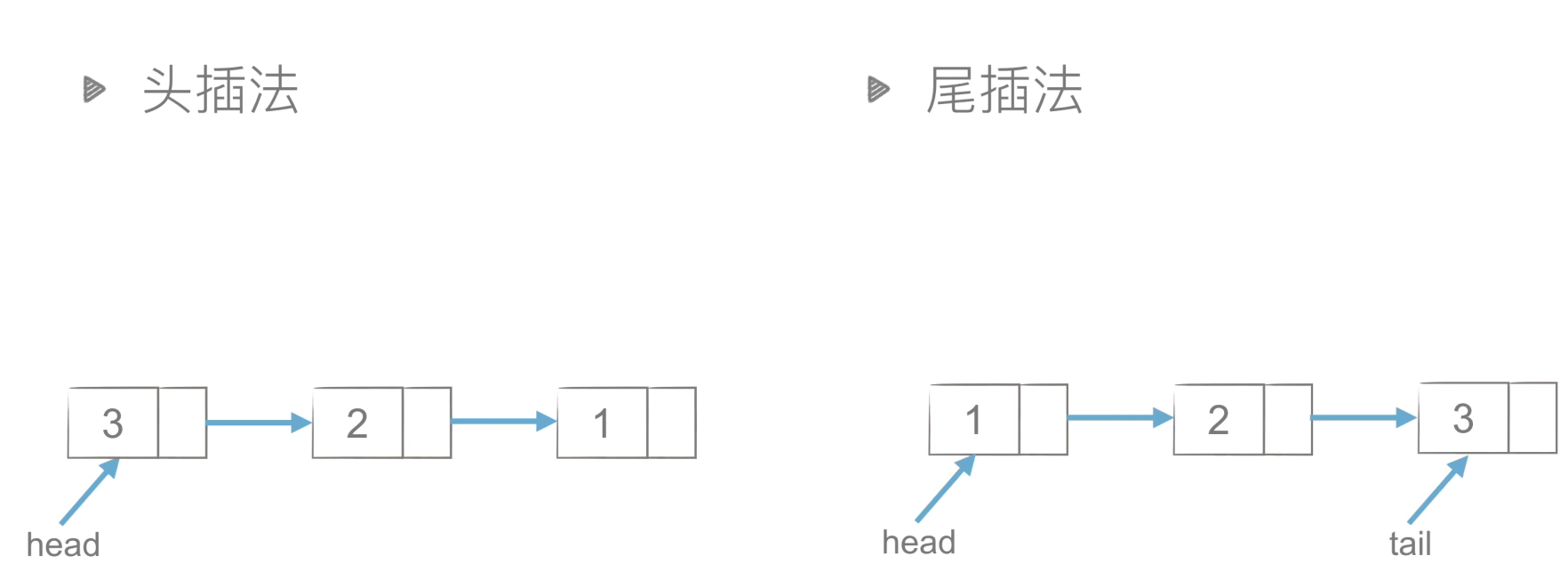
- 链表的创建
- 头插法:需要指向头节点的指针
- 尾插法:需要指向头节点和尾节点的指针
# 链表的创建
class Node:
def __init__(self,element): # 初始化结点(包括数据域和指针域)
self.element = element
self.next = None
# 头插法
def head_insert(li):
head = Node(li[0])
for i in li[1:]:
node = Node(i) # 创建新的结点
node.next = head
head = node
return head
head = head_insert([1,2,3,4,5,6])
print(head.element)
# 尾插法
def tail_insert(li):
head = Node(li[0])
tail = head
for i in li[1:]:
node = Node(i)
tail.next = node
tail = node
return head,tail
head,tail = tail_insert([1,2,3,4,5,6])
print(head.next.element,tail.element)
链表的插入和删除
链表的插入和删除操作的效率要高于列表
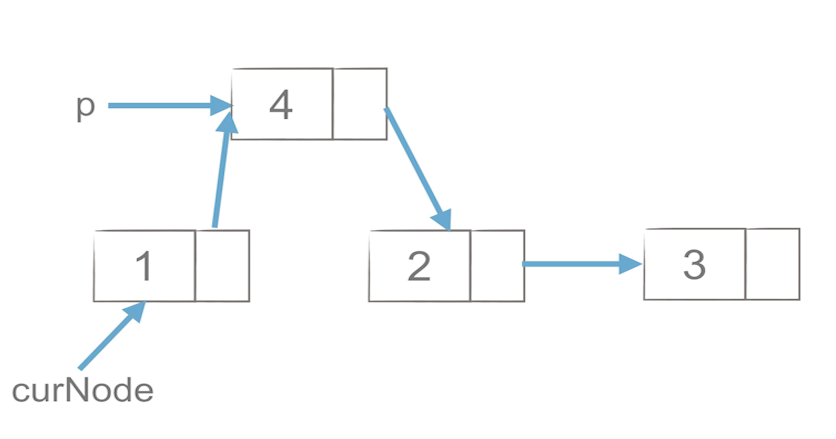
- 链表的插入:
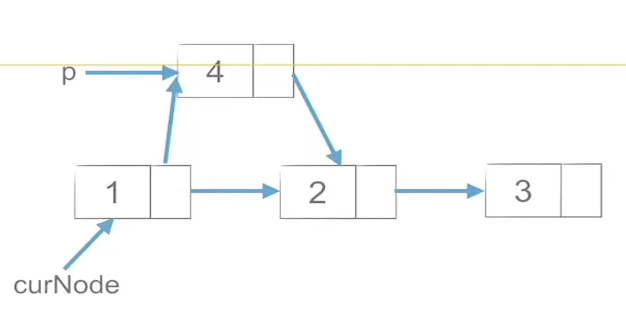
p.next = curNode.next
curNode.next = p
- 链表的删除:
![image]()
p=curNode.next
curNode.next = curNode.next.next
del p
双链表
双链表有两个指针(指向前一个结点的指针prior和指向后一个结点的指针next)
双链表的插入和删除
- 插入
![image]()
curNode.next.prior = p
p.next = curNode.next
curNode.next = p
p.prior = curNode
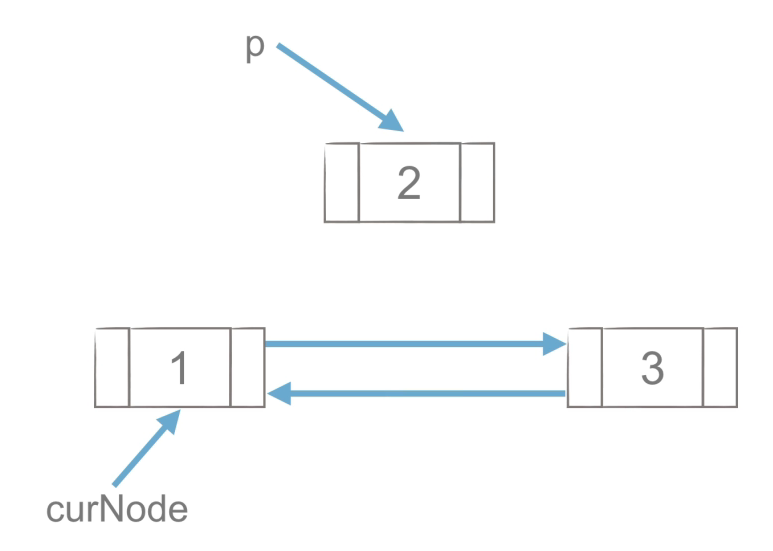
- 删除
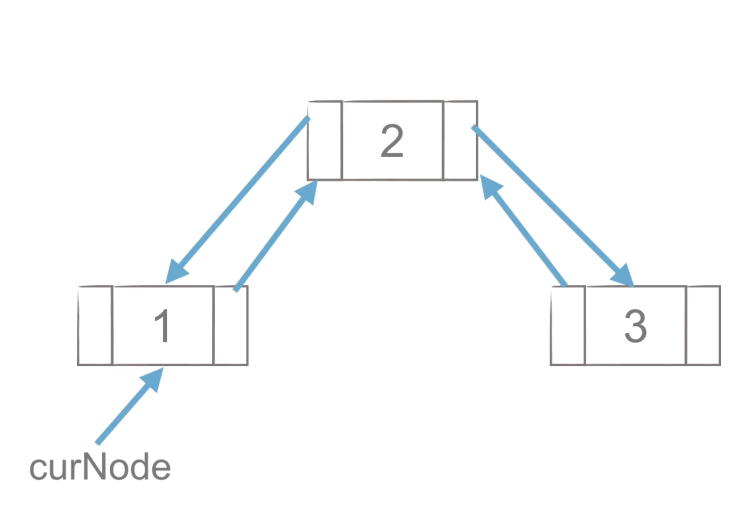
p = curNode.next
curNode.next = p.next
p.next.prior = curNode
del p
复杂度分析
顺序表(数组/列表)与链表
- 链表在插入和删除操作的时间效率要高于顺序表,顺序表在按下标查找元素的时间效率要高于链表
- 链表的内存可以更灵活的分配(不需要连续的且既定大小的空间)
哈希表(散列表)
通过哈希函数计算数据存储位置的数据结构,属于线性存储结构,通常支持如下操作:
- insert(key,value):插入键值对
- get(key):如果存在键为key的键值对则返回其value,否则返回空值
- delete(key):删除键为key的键值对
构成
①直接寻址表 ②哈希函数
哈希冲突
当有两个值通过哈希函数计算到了同一个位置上
python中的字典和集合以哈希表的形式实现的
哈希冲突解决方法
开放寻址法
通过哈希函数找到原本该存放的位置,当位置已有元素,接着通过以下方式进行空位的查找与存放;查找元素方法与存放元素方法必须一样。
- 线性探查法:如果位置i被占用,则探查i+1,i+2,……
- 二次探查法:如果位置i被占用,则探查i+12,i-12,i+22,i-22,……
- 二度哈希法:有n个哈希函数,当使用第一个哈希函数h1发生冲突时,则尝试使用h2,h3,……
拉链法
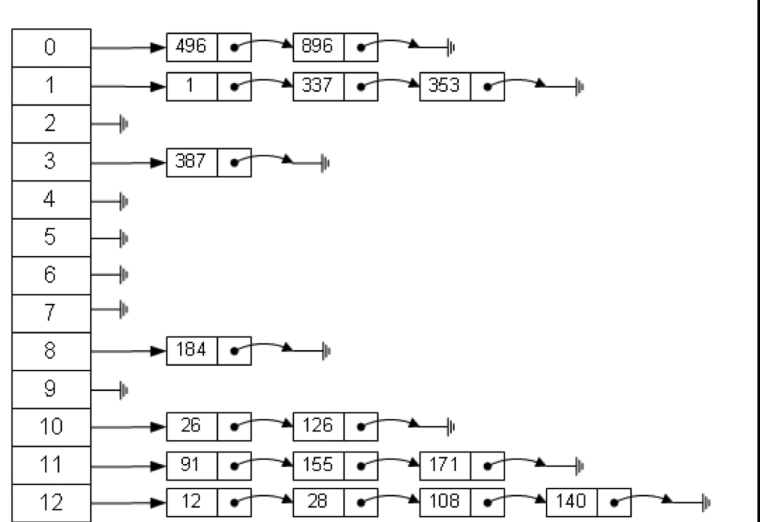
通过链表,将存放在同一位置的元素进行串联起来
直接寻址表(k的key为k)
- 原理
将可能的关键字范围建成一个长度为该范围的列表,关键字存放位置的下标即为该关键字的值(eg:2存放在下标为2的列表中)
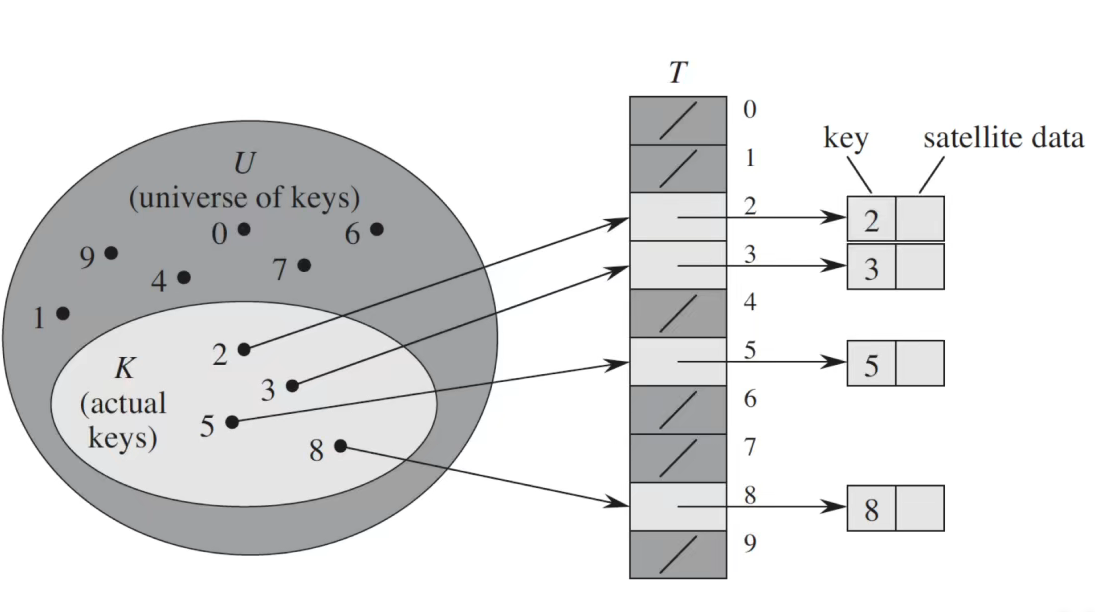
- 评价
优点:能够快速进行插入和删除操作
缺点:当关键字的域很大时,浪费空间;当域很多,而关键字较集中时(实际出现的key很少),浪费空间;无法处理关键字不为数字的情况
改进直接寻指标(哈希)(k的key为h(k))
- 思想
- 构建一个大小为m的列表
- 设置哈希函数h(k)使得关键域U映射在范围为[0,m-1]的列表中
哈希表的内部实现
# 链表功能的定义
class LinkList:
# 定义结点(包括数据域和指针域)
class Node:
def __init__(self,element=None):
self.element = element
self.next = None
# 迭代器的定义(必须有iter和next)
class LinkListIterator:
def __init__(self,head):
self.head = head
def __iter__(self):
return self
def __next__(self):
if self.head:
cur_node = self.head
self.head = cur_node.next
return cur_node.element
else:
raise StopIteration
# 链表的元素添加
def __init__(self,iterable=None):
self.head = None
self.tail = None
if iterable:
self.extend(iterable)
# 将元素进行拆分成单个元素
def extend(self,iterable):
for obj in iterable:
self.append(obj)
# 对单个元素进行添加
def append(self,obj):
s = LinkList.Node(obj)
if self.head:
self.tail.next = s
self.tail = s
else:
self.head = s
self.tail = s
# 对单个元素进行寻找
def find(self,obj):
for i in self:
if i == obj:
return True
else:
return False
# 设置链表迭代器
def __iter__(self):
return self.LinkListIterator(self.head)
# 输出
def __repr__(self):
return "<<"+",".join(map(str,self))+">>"
# 哈希数组的定义
class HashTable:
# 哈希数组
def __init__(self,size=101):
self.size = size
self.T = [LinkList() for i in range(self.size)]
# 哈希函数
def h(self,k):
return k % self.size
# 元素的插入
def insert(self,k):
key = self.h(k)
if self.T[key].find(k):
print("Duplicated Insert.")
else:
self.T[key].append(k)
hash = HashTable()
hash.insert(0)
hash.insert(1)
hash.insert(3)
hash.insert(102)
print(hash.T)
哈希表的应用
-
字典和集合都是通过哈希表来实现的
-
安全性上(将数据映射到128位的哈希值)
-
md5算法
-
SHA2算法(无法反推)
-
树
定义
树是一种非线性(一对多)且可以递归定义的数据结构
概念
-
根结点、叶子结点
- 根结点:第一个结点(无父结点)
- 叶子结点:无孩子的结点(无度的结点)
-
树的深度(高度)
-
树的度
整个结点中有最大度结点的度(结点的度:一个结点的分叉数)
树的实例
# 模拟文件系统(linus)
# 定义结点
class Node:
def __init__(self,name):
self.name = name
self.type = "dir"
self.childen = [] # 存放该结点的孩子结点
self.parent = None # 存放该结点的父结点
def __repr__(self):
return self.name
# 树结构
class FileSystemTree:
def __init__(self): # 初始化根目录
self.root = Node("/")
self.now = self.root
def mkdir(self,name): # 文件的创建
if name[-1] != "/":
name += "/"
newNode = Node(name)
self.now.childen.append(newNode)
newNode.parent = self.now
def ls(self): # 对当前文件的字文件进行查询
return self.now.childen
def cd(self,name): # 跳转文件
if name[-1] != "/":
name += "/"
for Name in self.now.childen:
if Name.name == name:
self.now = Name
return
raise ValueError("invalid dir")
file = FileSystemTree()
file.mkdir("bin")
file.mkdir("user")
file.cd("user")
file.mkdir("python")
print(file.ls())
二叉树
定义
- 每个结点的度都大于大于等于2
- 有左右结点孩子区分
存储形式
- 若为完全二叉树可采用顺序存储方式(如排序算法中的堆排序)
- 若不为完全二叉树可采用链式存储方式
结点的定义
class Node:
def __init__(self,name):
self.name = name
self.lchild = None # 左孩子
self.rchild = None # 右孩子
def __repr__(self): # 定义输出形式,默认输出地址
return self.name
a = Node("a")
b = Node("b")
c = Node("c")
d = Node("d")
e = Node("e")
root = a
a.lchild = c
a.rchild = b
b.rchild = d
print(root.rchild.rchild)
二叉树的遍历
遍历方式(主要思想:前中后序采用递归,层次采用队列)
- 前序遍历:EACBDGF
- 中序遍历:ABCDEGF
- 后续遍历:BDCAFGE
- 层次遍历:EAGCFBD
例子:
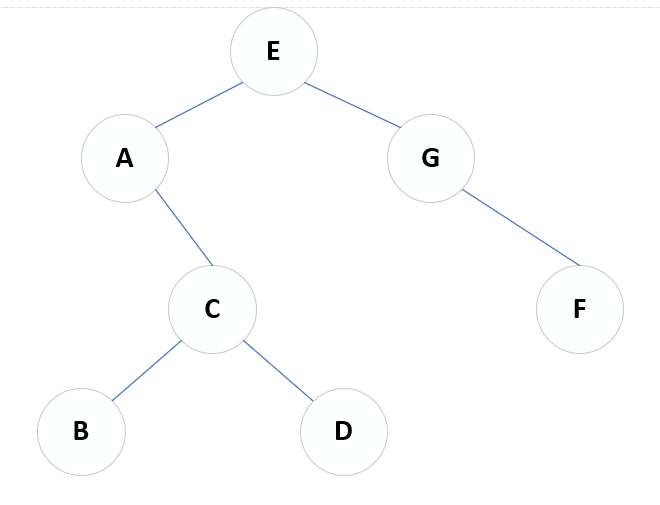
# 定义结点
class Node:
def __init__(self,element):
self.element = element
self.lchild = None
self.rchild = None
# 初始化各结点
e = Node("E")
a = Node("A")
g = Node("G")
c = Node("C")
f = Node("F")
b = Node("B")
d = Node("D")
# 结点关系存放
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f
root = e
# 递归遍历
# 前序遍历
def pre_order(root):
if root: # 遍历条件
print(root.element,end="") # 前序先打印
pre_order(root.lchild) # 遍历左孩子
pre_order(root.rchild) # 遍历右孩子
print("前序遍历为:",end="")
pre_order(root)
print()
# 中序遍历
def in_order(root):
if root:
in_order(root.lchild)
print(root.element,end="")
in_order(root.rchild)
print("中序遍历为:",end="")
in_order(root)
print()
# 后序遍历
def post_order(root):
if root:
post_order(root.lchild)
post_order(root.rchild)
print(root.element,end="")
print("后序遍历为:",end="")
post_order(root)
print()
# 层次遍历(队列思想)
from collections import deque
def level_order(root):
queue = deque() # 创建一个队列
if root: # 若存在根节点
queue.append(root) # 将根节点先入队
while len(queue)>0: # 判断队列是否还存在结点(不存在则所有元素全输出完毕)
node = queue.popleft() # 存在出队列,保存该结点(用以寻找其左右孩子)
print(node.element,end="") # 出队列的元素打印
if node.lchild: # 判断出队列元素是否存在左孩子
queue.append(node.lchild) # 存在则入队
if node.rchild: # 判断出队列元素是否存在右孩子
queue.append(node.rchild) # 存在则入队
print("层次遍历为:",end="")
level_order(root)
二叉搜索树(BST)
定义
所有左子树的值小于等于根节点,所有右子树的值大于等于根节点
操作
- 查询
# 二叉树插入算法
# 定义二叉树结点
class BiTreeNode:
def __init__(self,data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
# 定义二叉树方法
class BST:
# 初始二叉树无根结点
def __init__(self,li = None): # li为待插入元素的数组
self.root = None
if li: # 内部进行插入比较方便
for i in li:
self.insert_no_rec(i)
# 递归思想插入结点(效率会慢)
def insert(self,node,val): # node判断所插入的位置是否为空,val为待插入结点的值
if not node:
node = BiTreeNode(val) # 当找到的位置为空时,为val设置结点并存放在该位置中
elif val < node.data:
node.lchild = self.insert(node.lchild,val) # 递归插入,直到找到有空位置存放结点为止,返回插入节点本身
node.lchild.parent = node # 为结点设置父结点
elif val > node.data:
node.rchild = self.insert(node.rchild,val)
node.rchild.parent = node
return node
# 非递归思想,通过循环进行插入
def insert_no_rec(self,val):
p = self.root # 判断该二叉树是否存在根节点,p为指针,指向每个结点的位置
if not p: # 若不存在则将第一个结点存放在根节点处,该插入节点为根节点
self.root = BiTreeNode(val)
return
while True:
if val < p.data: # 当插入的值是否小于已有结点的值
if p.lchild: # 判断被比结点是否还有左孩子
p = p.lchild # 若有,则将指针移向被比结点的左孩子
else:
p.lchild = BiTreeNode(val) # 若无,则直接将结点存放在被比结点的左孩子处
p.lchild.parent = p # 设置插入结点的父亲结点
return
elif val > p.data:
if p.rchild:
p = p.rchild
else:
p.rchild = BiTreeNode(val)
p.rchild.parent = p
return
else:
return
# 二叉树遍历方法
# 中序遍历
def pre_order(self,node):
if node:
self.pre_order(node.lchild)
print(node.data, end="")
self.pre_order(node.rchild)
# 二叉树的查询
# 递归思想
def query(self,node,val):
if not node:
return None
else:
if node.data > val:
return self.query(node.lchild,val) # 只需要进入递归函数,递归函数执行完成后无需再往下执行原本的代码行(有return)
elif node.data < val:
return self.query(node.rchild,val) # 没有return返回不了True or None
else:
return True
# 非递归思想
def query_no_rec(self,val):
p = self.root
while p:
if p.data > val:
p = p.lchild
elif p.data < val:
p = p.rchild
else:
return True
return None
import random
li = list(range(0,500,2))
random.shuffle(li)
tree = BST(li)
# tree.pre_order(tree.root)
print(tree.query_no_rec(6))
print(tree.query(tree.root,6))
- 插入
# 二叉树插入算法
# 定义二叉树结点
class BiTreeNode:
def __init__(self,data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
# 定义二叉树方法
class BST:
# 初始二叉树无根结点
def __init__(self,li = None): # li为待插入元素的数组
self.root = None
if li: # 内部进行插入比较方便
for i in li:
self.insert_no_rec(i)
# 递归思想插入结点(效率会慢)
def insert(self,node,val): # node(用来递归的)判断所插入的位置是否为空,val为待插入结点的值
if not node:
node = BiTreeNode(val) # 当找到的位置为空时,为val设置结点并存放在该位置中
elif val < node.data:
node.lchild = self.insert(node.lchild,val) # 递归插入,直到找到有空位置存放结点为止,返回插入节点本身
node.lchild.parent = node # 为结点设置父结点
elif val > node.data:
node.rchild = self.insert(node.rchild,val)
node.rchild.parent = node
return node
# 非递归思想,通过循环进行插入
def insert_no_rec(self,val):
p = self.root # 判断该二叉树是否存在根节点,p为指针,指向每个结点的位置
if not p: # 若不存在则将第一个结点存放在根节点处,该插入节点为根节点
self.root = BiTreeNode(val)
return
while True:
if val < p.data: # 当插入的值是否小于已有结点的值
if p.lchild: # 判断被比结点是否还有左孩子
p = p.lchild # 若有,则将指针移向被比结点的左孩子
else:
p.lchild = BiTreeNode(val) # 若无,则直接将结点存放在被比结点的左孩子处
p.lchild.parent = p # 设置插入结点的父亲结点
return
elif val > p.data:
if p.rchild:
p = p.rchild
else:
p.rchild = BiTreeNode(val)
p.rchild.parent = p
return
else:
return
# 二叉树遍历方法
# 中序遍历
def pre_order(self,node):
if node:
self.pre_order(node.lchild)
print(node.data, end="")
self.pre_order(node.rchild)
import random
li = list(range(50))
random.shuffle(li)
tree = BST(li)
tree.pre_order(tree.root)
- 删除
- 三种情况(都要判断删除的结点是否为根节点)
- 删除的对象为叶子结点:直接删除
- 删除的对象有一个孩子结点:将孩子给删除对象的父亲结点,再对对象进行删除(注意,当删除的是根结点时,要重新赋值根节点root)
- 删除的对象有两个孩子结点:找到左孩子的最大结点/右孩子的最小结点替换删除的结点,转化为删除找到的那个结点
- 三种情况(都要判断删除的结点是否为根节点)
# 二叉树插入算法
# 定义二叉树结点
class BiTreeNode:
def __init__(self,data):
self.data = data
self.lchild = None
self.rchild = None
self.parent = None
# 定义二叉树方法
class BST:
# 初始二叉树无根结点
def __init__(self,li = None): # li为待插入元素的数组
self.root = None
if li: # 内部进行插入比较方便
for i in li:
self.insert_no_rec(i)
# 递归思想插入结点(效率会慢)
def insert(self,node,val): # node判断所插入的位置是否为空,val为待插入结点的值
if not node:
node = BiTreeNode(val) # 当找到的位置为空时,为val设置结点并存放在该位置中
elif val < node.data:
node.lchild = self.insert(node.lchild,val) # 递归插入,直到找到有空位置存放结点为止,返回插入节点本身
node.lchild.parent = node # 为结点设置父结点
elif val > node.data:
node.rchild = self.insert(node.rchild,val)
node.rchild.parent = node
return node
# 非递归思想,通过循环进行插入
def insert_no_rec(self,val):
p = self.root # 判断该二叉树是否存在根节点,p为指针,指向每个结点的位置
if not p: # 若不存在则将第一个结点存放在根节点处,该插入节点为根节点
self.root = BiTreeNode(val)
return
while True:
if val < p.data: # 当插入的值是否小于已有结点的值
if p.lchild: # 判断被比结点是否还有左孩子
p = p.lchild # 若有,则将指针移向被比结点的左孩子
else:
p.lchild = BiTreeNode(val) # 若无,则直接将结点存放在被比结点的左孩子处
p.lchild.parent = p # 设置插入结点的父亲结点
return
elif val > p.data:
if p.rchild:
p = p.rchild
else:
p.rchild = BiTreeNode(val)
p.rchild.parent = p
return
else:
return
# 二叉树遍历方法
# 中序遍历
def pre_order(self,node):
if node:
self.pre_order(node.lchild)
print(node.data, end="")
self.pre_order(node.rchild)
# 二叉树的查询
# 递归思想
def query(self,node,val):
if not node:
return None
else:
if node.data > val:
return self.query(node.lchild,val) # 只需要进入递归函数,递归函数执行完成后无需再往下执行原本的代码行(有return)
elif node.data < val:
return self.query(node.rchild,val) # 没有return返回不了True or None
else:
return node
# 非递归思想
def query_no_rec(self,val):
p = self.root
while p:
if p.data > val:
p = p.lchild
elif p.data < val:
p = p.rchild
else:
return p
return None
# 删除算法
def __delete_condition_1_(self,node): # 情况一:当删除的是叶子节点时
if not node.parent: # 当该叶子结点是根节点时
self.root = None
elif node == node.parent.lchild: # 判断该叶子结点是该结点父亲的左孩子还是右孩子
node.parent.lchild = None
else:
node.parent.rchild = None
def __delete_condition_21_(self,node): # 情况二1:删除的结点结点只有一个孩子(左孩子)
if not node.parent:
self.root = node.lchild
node.lchild.parent = None
elif node == node.parent.lchild:
node.parent.lchild = node.lchild
node.lchild.parent = node.parent
else:
node.parent.rchild = node.lchild
node.lchild.parent = node.parent
def __delete_condition_22_(self,node): # 情况二2:删除的结点结点只有一个孩子(右孩子)
if not node.parent:
self.root = node.rchild
node.rchild.parent = None
elif node == node.parent.lchild:
node.parent.lchild = node.rchild
node.rchild.parent = node.parent
else:
node.parent.rchild = node.rchild
node.rchild.parent = node.parent
# 结点的删除操作
def delete(self,val):
node = self.query_no_rec(val)
if not self.root and not node: # 判断是否存在树以及是否有删除的该结点
return False
if not node.lchild and not node.rchild: # 情况一:当为叶子节点时
self.__delete_condition_1_(node)
elif not node.rchild: # 情况二1:当只有一个左孩子时
self.__delete_condition_21_(node)
elif not node.lchild: # 情况二2:当只有一个右孩子时
self.__delete_condition_22_(node)
else: # 情况三:左右孩子都有时
min_lchild = node.rchild # 找到删除结点右子树的最小结点
while min_lchild.lchild:
min_lchild = min_lchild.lchild
node.data = min_lchild.data # 直接将删除部分的数据域换成替换的数据域(好处,不用再重新指回左右孩子)
if min_lchild.rchild: # 当替换的结点有右孩子时
self.__delete_condition_22_(min_lchild)
else: # 当替换的结点为叶子节点时
self.__delete_condition_1_(min_lchild)
bst = BST([2,5,3,4,1,9,7,8,6])
bst.pre_order(bst.root)
print()
bst.delete(4)
bst.delete(8)
bst.pre_order(bst.root)
AVL树(不是算法考察重点)
二叉树平均时间效率为O(logn),有时会出现极端情况(即形状呈现线性结构)。解决措施:随机化插入、AVL树
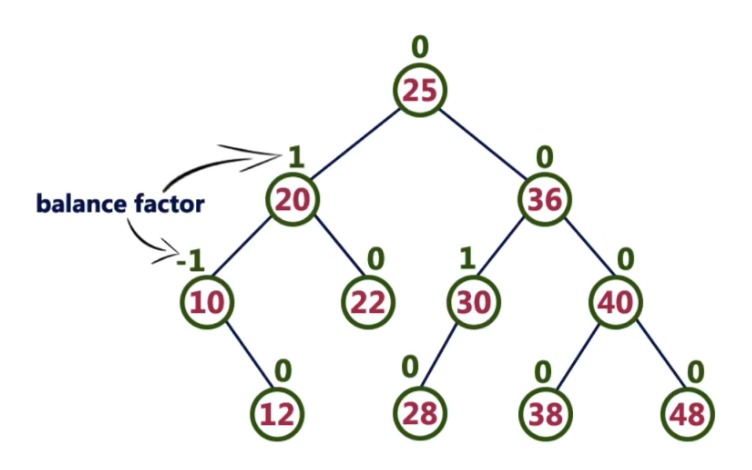
定义
是一棵自平衡的二叉搜索树
性质
- 根的左右子树的高度差的绝对值不超过1
- 根的左右子树都是平衡二叉树
旋转
- 插入一个新的结点时,可能会破坏AVL树的平衡,可通过旋转操作来进行修正
- 插入的结点只可能导致其中树的一半造成不平衡想象,且插入后结点的高度差不超过3
不平衡的四种情况
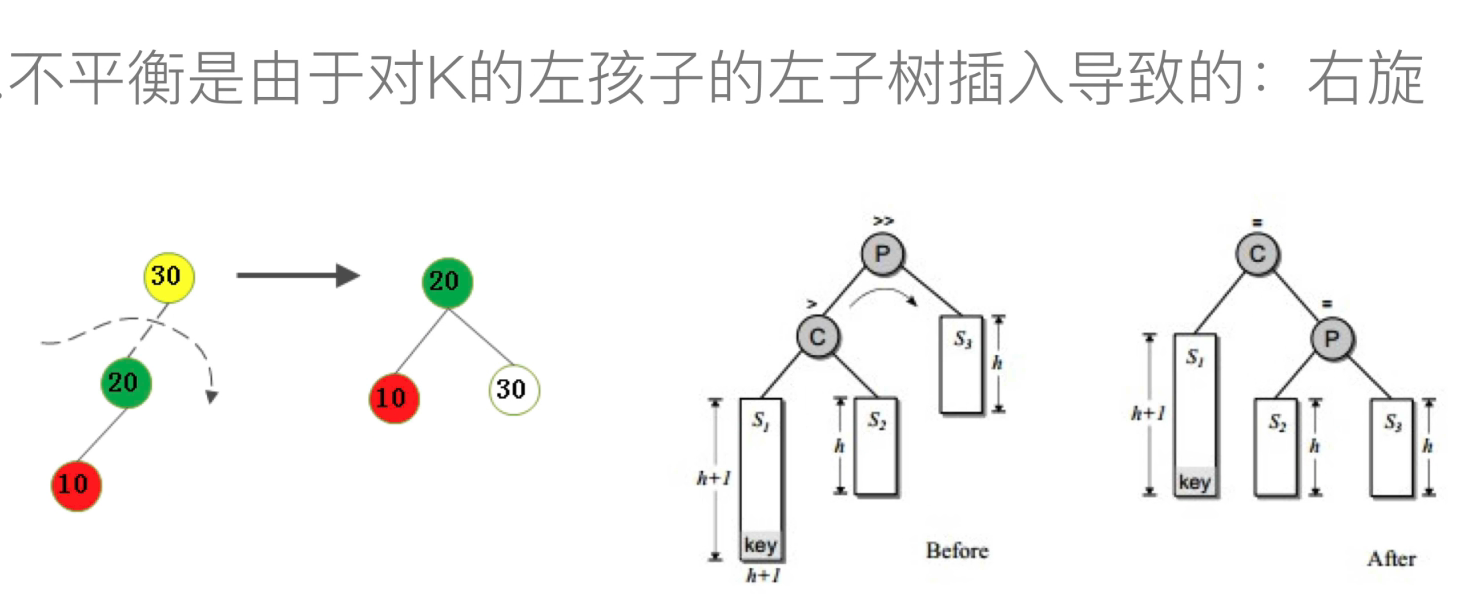
-
左左:右旋
![image]()
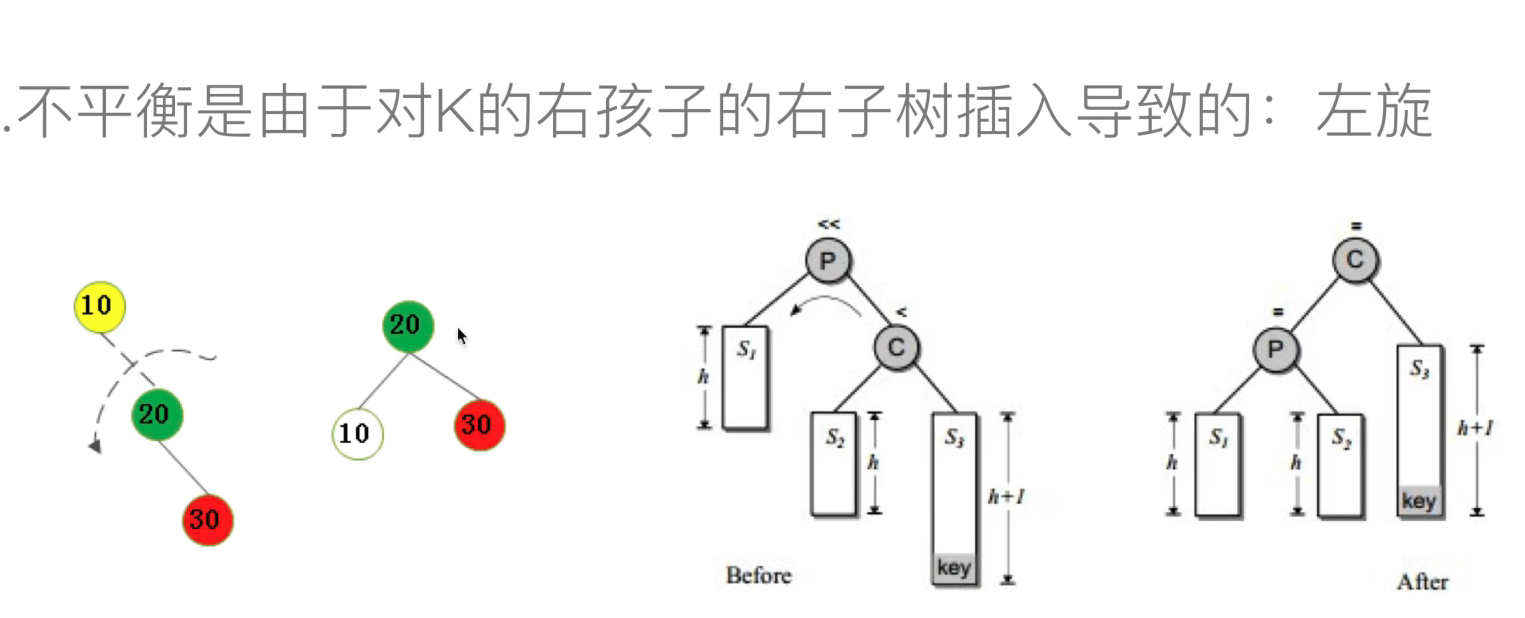
-
右右:左旋
![image]()
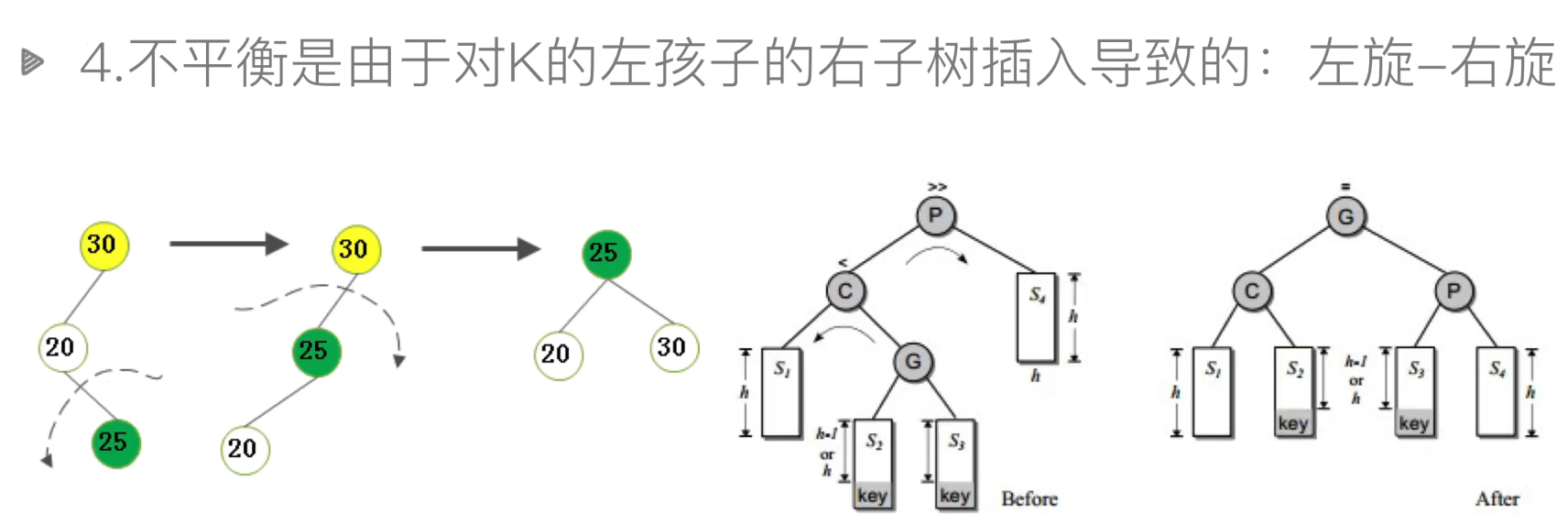
-
左右:左右旋
![image]()
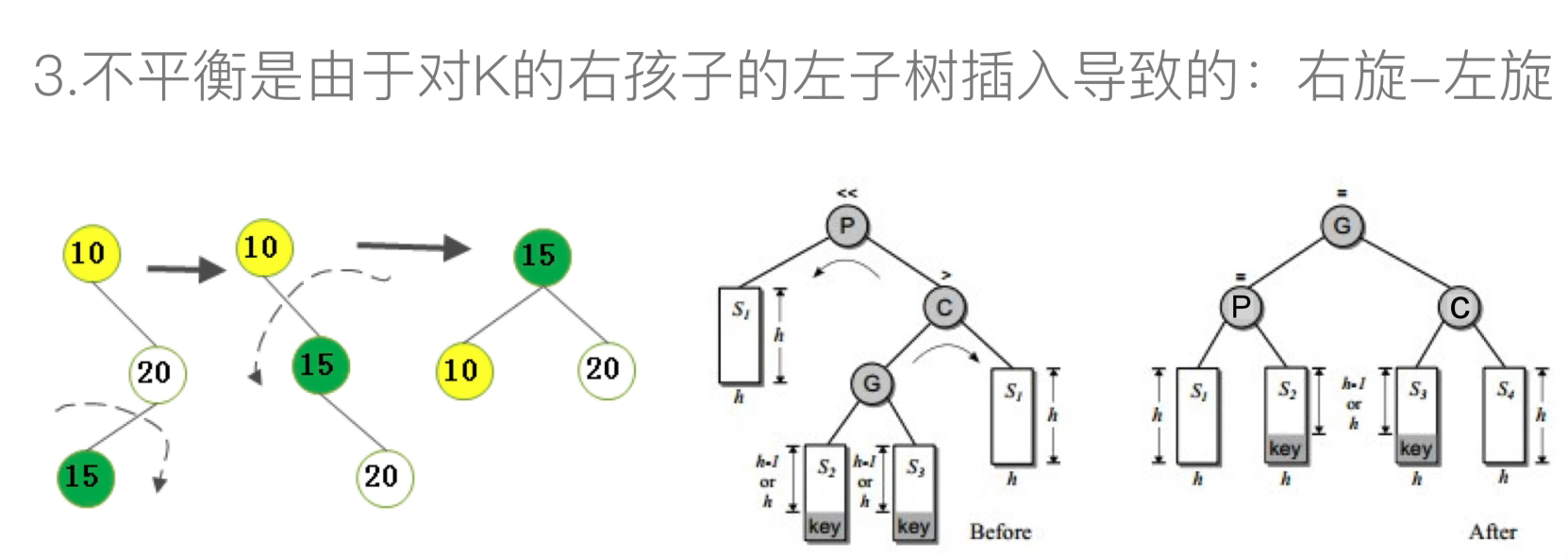
-
右左:右左旋
![image]()
旋转的实现
from main import BiTreeNode,BST # 导入先前写的二叉树(结点的生成和二叉树的遍历等方法)
class AVLNode(BiTreeNode):
def __init__(self,data):
BiTreeNode.__init__(self,data)
self.bf = 0 # 在二叉树结点属性的基础上加上一个结点左右孩子的高度差变量
class AVLTree(BST):
def __init__(self,li = None):
BST.__init__(li)
def rotate_right(self,p,c): # 不平衡情况一根左左:右转(p为由下往上找第一个bf大于1的结点,c则为该分支中p的下一个结点)
s2 = c.rchild # 若c(代替根节点,成为根节点的结点)存在右孩子,则把右孩子给根节点,根节点变为c的右孩子
if s2:
p.lchild = s2
s2.parent = p
c.rchild = p
p.parent = c
p.bf = 0 # 更改变化后各节点的高度差
c.bf = 0
def rotate_left(self,p,c): # 不平衡情况二根右右:左转(与情况一类似)
s2 = c.lchild
if s2:
p.rchild = s2
s2.parent = p
c.lchild = p
p.parent = c
p.bf = 0
c.bf = 0
def rotate_left_right_(self,p,c): # 不平衡情况三根左右:左右转(p为由下往上找第一个bf大于1的结点,c则为该分支中p的下一个结点)
g = c.rchild # 找到g(替换根节点,成为根节点的结点)
# 判断待成为根节点的结点是否存在左右孩子(左孩子成为其父结点的右孩子,父结点成为其左孩子;右孩子成为根节点的左孩子,根结点成为其右孩子)
if g.lchild:
g.lchild.parent = c
c.rchild = g.lchild
g.lchild = c
c.parent = g
if g.rchild:
g.rchild.parent = p
p.lchild = g.rchild
g.rchild = p
p.parent = g
# 判断待成为根节点的结点原始的高度差,若为1,则右孩子与根节点的右孩子高度差一样,左孩子比父结点左孩子的高度差小1;若为-1,则相反;
# 若为零,则在插入过程中,插入的是g(待成为根节点的结点),各结点的左右孩子高度差为0
if g.bp > 0:
c.bp = -1
p.bp = 0
elif g.bp < 0:
c.bp = 0
p.bp = 1
else:
c.bp = 0
p.bp = 0
def rotate_right_left(self,p,c): # 不平衡情况四根右左:右左转(与情况三类似)
g = c.lchild
if g.lchild:
g.lchild.parent = p
p.rchild = g.lchild
g.lchild = p
p.parent = g
if g.rchild:
g.rchild.parent = c
c.lchild = g.rchild
g.rchild = c
c.parent = g
if g.bp > 0:
p.bp = -1
c.bp = 0
elif g.bp < 0:
p.bp = 0
c.bp = 1
else:
p.bp = 0
c.bp = 0
# g.bp为原本的数,不改变
插入操作
- 原理思想:当插入在左(右)子树上,该结点的父结点的balance factor的值-(+)1,若从左(右)子树上到(子)树的根节点,则该根节点-(+)1,当中间balance factor的值有超过1时,进行旋转操作,当旋转后的根节点不为0时,进行进行向上的balance factor值的变化,直到达到整棵树的根节点或者当有个结点-(+)1为0时,停止向上更改balance factor。每插入一个结点都要更改其向上分支的balance factor值
B树(B-Tree)(二叉搜索树扩展应用)
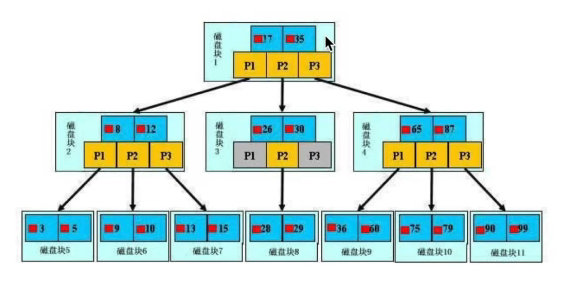
定义
B树是一棵自平衡的多路搜索树。常用于数据库的索引
原理
如图:一块地方存放两个数据域,37,25,(分2+1个分支),当新加入的数据域小于17,则存放在左边,若大于17小于35时,存放在中间,若大于35时,则存放在右边。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号