队列、栈算法笔记

今天说说队列和栈

队列

概念

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出（First in First Out）的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为队头。假设队列是q=（a1,a2,…,an），那么a1就是队头元素，而an是队尾元素。这样我们就可以删除时，总是从a1开始，而插入时，列在最后。这也比较符合我们通常生活中的习惯，排在第一个的优先出列，最后来的当然在队伍的最后。(如图)

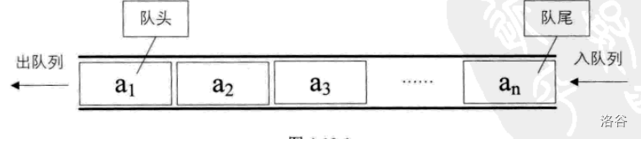
实现

定义：

#include<queue>
queue<数据类型>队列名

常用函数：

q.empty()// 如果队列为空返回true，否则返回false
q.size() // 返回队列中元素的个数  
q.pop()  //删除队列首元素但不返回其值  
q.front()  // 返回队首元素的值，但不删除该元素 
q.push(X) //在队尾压入新元素 ，X为要压入的元素
q.back() //返回队列尾元素的值，但不删除该元素

例题：约瑟夫问题

题目描述

n个人围成一圈，从第一个人开始报数,数到m的人出列，再由下一个人重新从 1开始报数，数到 m的人再出圈，依次类推，直到所有的人都出圈，请输出依次出圈人的编号。

输入格式

输入两个整数 n,m。

输出格式

输出一行 nn 个整数，按顺序输出每个出圈人的编号。

输入

10 3

输出

3 6 9 2 7 1 8 5 10 4

先上代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,bs;
queue<int>xss;
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++)
		xss.push(i);
	for(int i=1;!xss.empty();i++)
	{
		if(i%m!=0)
		{
			bs=xss.front();
			xss.pop();
			xss.push(bs);
			bs=0;
		}
		else
		{
			cout<<xss.front()<<" ";
			xss.pop();
		}
	}
	return 0;
}

思路：此题我认为比较水（可我还是卡了好一会）

先输入n和m，然后用for和push函数创建一个n到m的初始队列。接着不断循环，结束条件是队列为空（即人全出列）然后用if判断是否报到m，没报到把队首扔回队尾，是的话输出并在队列中删除。

栈

概念

栈，是一种存储受限的线性数据结构，在存储和访问数据的时候只能访问栈的一端。栈类似于一摞盘子，只能拿去最上面的盘子，也只能把盘子放到最上面。由于这种特点，栈是一种后进先出（Last in / First out, LIFO）的数据结构。

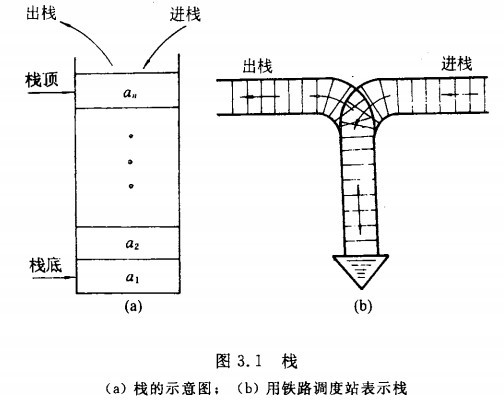
实现

定义：

#include<stack>
stack<数据类型>  栈名;

常用函数：

s.empty()//如果栈为空返回true，否则返回false  
s.size()//返回栈中元素的个数  
s.pop()//删除栈顶元素但不返回其值  
s.top()//返回栈顶的元素，但不删除该元素  
s.push(X)//在栈顶压入新元素，参数X为要压入的元素

例题：后缀表达式

题目描述

所谓后缀表达式是指这样的一个表达式：式中不再引用括号，运算符号放在两个运算对象之后，所有计算按运算符号出现的顺序，严格地由左而右新进行（不用考虑运算符的优先级）。

如：3(5–2)+7对应的后缀表达式为：3．5．2．-7．+@。’@’为表达式的结束符号。‘.’为操作数的结束符号。

输入格式

输入：后缀表达式

输出格式

输出：表达式的值

输入

3.5.2.-*7.+@

输出

16

代码first：

#include<bits/stdc++.h>
using namespace std;
stack<int>q;
string s;
int main()
{
	cin>>s;
	int a=0;
	int i,j;
	for(int k=0;k<=s.length();k++)
	{
		if(s[k]=='@')
			break;
			else if (s[k]=='.')
				q.push(a),a=0;
				else if(s[k]<='9'&&s[k]>='0')
					a=a*10+(s[k]-'0');
					else
					{	
						i=q.top(),q.pop();
						j=q.top(),q.pop();
						if(s[k]=='-')
							q.push(j-i);
						if(s[k]=='+')
							q.push(j+i);
						if(s[k]=='*')
							q.push(j*i);
						if(s[k]=='/')
							q.push(j/i);
					}
	}
	cout<<q.top()<<endl;
	return 0;
}

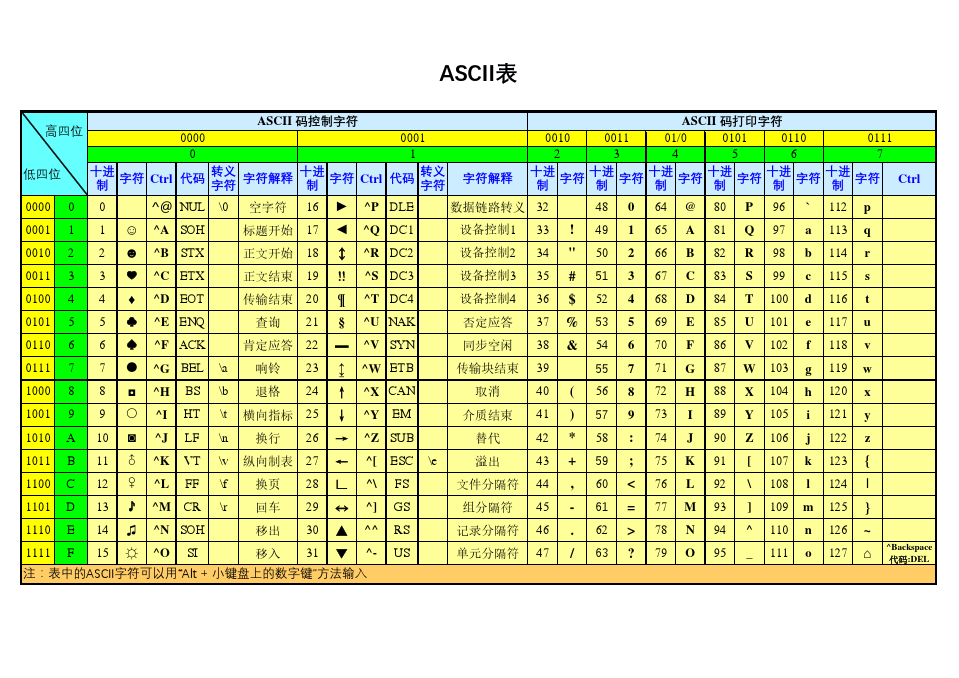
(ASCII码有点忘了所以再在这里贴一下)

思路：

把所有的数字先放入一个栈中，然后一个个识别运算符，识别到一个就拿出两个数进行运算，最后栈的最顶一个一定是结果。