Python实现7个排序算法

复习整理7个排序算法，注释和说明是自己的表达，若看出有错，欢迎找我改错。

冒泡排序

冒泡排序是最简单的排序之一，其大体思想就是通过与相邻元素的比较和交换来把大的数交换到最后面。

#冒泡排序，对列表进行升序排序
def bubble_sort(alist):
    #相邻两个元素进行比较，如果发现位置错误（前一个比后一个大）则进行交换
    for k in range(len(alist)-1):
        count = 0  #用于判断列表原来是否有序
        for i in range(len(alist)-1-k):
            # 冒泡
            if alist[i]>alist[i+1]:
                alist[i],alist[i+1] = alist[i+1],alist[i]
                count += 1
        if count == 0:
            break       

alist = [6,43,57,24,34,46]
bubble_sort(alist)
print(alist)

 

稳定性：如果遇到相同的两个元素，排序完和排序之前这两个元素的相对位置还是相同的，则这个排序算法是稳定的
最优时间复杂度：O(n)注：就是数组原本就是有序的情况

最坏时间复杂度O(n^2)

稳定性：稳定

 

插入排序

大体思想就是数组分为已排序和待排序两部分，通过插入待排序部分的数字到前面已排序的数组完成排序。

unsort = [0,10,90,50,60,30,55,1,-1]
def insert_sort(unsort):
    for i in range(1,len(unsort)):# 从第二个开始，假装第一个数字为有序序列
        while i>0:# i=0为最坏情况，要比较的这个数字比前面有序序列里的数都要小
            if unsort[i]<unsort[i-1]:
                # 拿新的未比较的数与前面有序序列的值进行比较，在合适位置插入，或者说是一路替换到合适它的坑
                unsort[i], unsort[i-1] = unsort[i-1], unsort[i]
            else:
                # 当它比有序序列的值大时意味着已经到了合适它的坑~
                break
            i -= 1
    print(unsort)

insert_sort(unsort)

 

最坏时间复杂度O(n^2)
最优时间复杂度O(n)
稳定性：稳定，比如可以想想数组[17, 20, 31, 44, 54, 55, 77, 93, 77,226]

 

选择排序

每次循环选出待排序数组的最大值（最小值），替换到正确位置。然后寻找次大或次小的数值继续替换，直到数组有序。

def select_sort(alist):
    n = len(alist)
    for k in range(n-1):
        #剩余列表最小值索引
        min_index = k
        for i in range(k+1,n):
            if alist[min_index]>alist[i]:
                min_index = i
        if min_index != k:  #如果元素不在这个位置才要交换
            alist[k],alist[min_index] = alist[min_index],alist[k]
alist = [10,4,56,7,2]
select_sort(alist)
print(alist) 

最坏时间复杂度O(n^2)

最优时间复杂度O(n^2)

稳定性：不稳定 也可以以数组[17, 99, 31, 54, 43, 55, 99, 77]为例，当选择的是最大值时。是不是不稳定呢？

 

归并排序

先分解数组到最小，然后排序整合。

比如：[2,3,4,1]

分解（最后一次分解）：[2],[3],[4],[1]

排序整合：   [2,3],[1,4]

　　　　　　[1,2,3,4]

def merg_sort(alist):
    n = len(alist)
    # 递归出口 分解到最小（即一个元素）
    if n<=1:
        return alist
    mid = n //2
    left_li = merg_sort(alist[0:mid])  # 递归分解左边的列表，直到递归出口
    right_li = merg_sort(alist[mid:])  # 递归分解右边的列表，直到递归出口
    # 合并，并排序结果列表
    result = []  # 结果
    left_pointer,right_pointer = 0,0  # 两边列表的指针
    while left_pointer<len(left_li) and right_pointer<len(right_li):  # 当左指针小于左列表且右指针小于右列表时
        if left_li[left_pointer] < right_li[right_pointer]:  # 当左列表当前指针指向的值小于右列表当前指针指向的值
            result.append(left_li[left_pointer])  # 小的值先加入结果列表
            left_pointer += 1  # 已经使用过当前指针的值，指针需要加一
        else:
            result.append(right_li[right_pointer])
            right_pointer += 1
    
    # 退出循环后，将不为空的列表的剩余元素添加到result后
    result += left_li[left_pointer:]
    result += right_li[right_pointer:]
    
    # 返回排序好的列表
    return result

alist = [54,26,93,17,77,31,44,55]
print(merg_sort(alist))

 最优时间复杂度O(nlogn)

最差时间复杂度O(nlogn)

稳定性：稳定

 

快速排序

 先选中数组一个数为基准数，然后以这个数为准，左边放比它小的数，右边放比它大的数。然后对其左右的数组继续这个操作，直到数组有序

def quick_sort(alist,start,end):
    #递归退出条件
    if start >= end:
        return
    #基准数
    mid = alist[start]
    low = start
    high = end
    while low<high:
        #从右到左alist[high]>mid 则high-=1
        while low<high and alist[high]>mid:
            high -= 1
        #当alist[high]<mid时，将high索引对应的元素赋值给low
        alist[low] = alist[high]
        print('high',alist)
        
        #从左到右alist[low]<mid 则low+=1
        while low<high and alist[low]<mid:
            low += 1
        alist[high] = alist[low]
        print('low',alist)
    #将基准数放到对应位置,因为此时随着low的增加到了low=high即刚好放mid
    alist[low] = mid
    
    #比基准数小的即左边的数据，要重复调用quick_sort()
    quick_sort(alist,start,low-1)
    #比基准数大的即右边的数据，要重复调用quick_sort()
    quick_sort(alist,low+1,end)

    
alist = [54,26,93,17,77,31,44,55,20]
quick_sort(alist,0,len(alist)-1)    
print(alist)

最优时间复杂度O(nlog2(n))
最差时间复杂度O(n^2)注：就是数组原本就是有序的情况
稳定性：不稳定比如[54,26,93,17,77,31,44,55,(20,1),(20,2)]

 

希尔排序

和插入排序很像，只不过有一个gap的存在。它是让数组按gap长度分裂子数组，然后就是按插入排序进行排序。

当最后gap=1时确实也就是插入排序了，可以减少像直接插入排序算法的数字间比较次数

def shell_sort(alist):
    n = len(alist)
    #设置间隔为n//2
    gap = n//2
    while gap > 0:  # gap会不断减小，当gap=1时就相当于是插入排序了
        for j in range(gap,n):  #从gap开始，因为之前的元素被当做每分组已排好序的元素
            i = j  #j是递增1的，表示一次循环就完成所有假设分组的排序
            while i > 0:
                #插入排序算法
                if alist[i-gap] > alist[i]:
                    alist[i-gap], alist[i] = alist[i],alist[i-gap]
                    i -= gap
                else:
                    break
        #gap不断减小
        gap //= 2

alist = [54,26,93,17,77,31,44,55,20]
shell_sort(alist)
print(alist)

 最优时间复杂度O(n^(1.3))
最差时间复杂度O(n^2)
稳定性：不稳定

 

堆排序

首先要明白这个叫最大堆的东东：

 

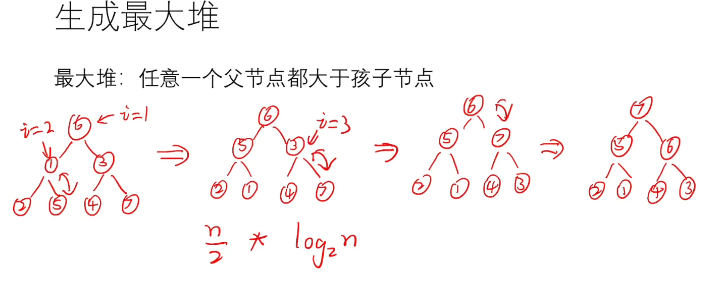
最大堆的生成就是不断地将数值较大的子节点替换到父节点，直到满足最大堆的定义

上面就是堆排序算法，不断将根节点（最大值，所以结果是降序的）pop出来后用最后一位节点填上，然后继续计算最大堆。如此反复，直到存储堆列表的长度为1。

 

def adjust_heap(l, parent):
    '''
    l为要构造的最大堆（二叉树）
    parent为父节点的index
    视l为一棵树，第一个元素为树的根节点
    '''
    length = len(l)
    parent_value = l[parent]  #获取父节点的值
    child = parent * 2 + 1  #获取左节点的index
    while child < length:  #存在左节点，因为l是列表来的，当child的index超过length时说明这个节点没有子节点
        if child + 1 < length and l[child + 1] > l[child]: #判断右节点值是否比左节点大
            child += 1  #index换成右节点，用于后面和父节点比较，就是左右子节点最大的与父节点作比较

        if l[child] <= parent_value:
            break
        l[parent] = l[child]  #当子节点值大于父节点时，将子节点和父节点的值互换
        parent = child  #子节点变父节点
        child = 2 * parent + 1  
        #当前parent的子节点，继续当前循环，寻找还有没有比这个父节点大的子节点，
        #大的子节点直接覆盖父节点是没有问题的，因为parent_value保存了最初被覆盖的值
    #print(l)
    l[parent] = parent_value  # 当子节点没有比父节点大的值时，把最初被替换的值替换到子节点


def heap_sort(l, result=None):
    if len(l) == 1:  #递归终止条件
        result.append(l[0])
        return l
    if result is None:
        result = []
    parents = [i for i in range(len(l))]
    parents.reverse()
    #print(parents)
    #parents为lindex的逆序
    for parent in parents:
        adjust_heap(l, parent)  #从最后的一个子节点开始，构造最大堆

    tmp = l[0]  #构造好最大堆后，取根节点（最大值）
    l[0] = l[len(l) - 1]  #用最后一个节点代替根节点
    l[len(l) - 1] = tmp  #根节点的值放到最后一个节点

    result.append(l.pop())  #把最大值pop到result
    heap_sort(l, result)  #递归调用，直到l的长度为1
    return result
def test():
    l = [99,7, 4, 5, 3, 6, 9, 7, 8, 0]
    print (l)
    print (heap_sort(l))
test()

 最优时间复杂度O(nlogn)
最差时间复杂度O(nlogn)
稳定性：不稳定