Soluton Set - ZJOI历年真题
大概是不会再写了。
ZJOI2022 Day1T1
tag:组合计数,容斥
假设固定了第二棵树,只考虑第一棵树,一个平凡的 DP 是:定义 \(dp_{i,j}\) 为考虑了前 \(i\) 个点,其中有 \(j\) 个非叶结点的方案数。但是这里并不容易转移,我们每次只能选择一个点的父亲,然后选择是否把一个点加入“非叶结点集合”中,但并不能保证这个点真的是非叶结点。当然这个问题很容易解决,容斥就可以。
再考虑两棵树的情况,会发现不好像之前那样按顺序转移,因为要同时选择一个点在两棵树上的父亲,而总有一棵树还没有确定。这时不一定就要改变转移方式,可以在初始值上做手脚。可以设计一个这样的 DP:\(dp_{i,j,k}\) 表示前 \(i-1\) 个点中有 \(j\) 个第一棵树的非叶结点(和上面说的一样,是一个“非叶结点集合”),后 \(n-i\) 个点中有 \(k\) 个第二棵树的非叶结点的情况数。当然是在容斥的意义下。初始值设置为 \(dp_{1,1,k}=1,\forall k=1,2,\cdots,n-1\),最后的答案就是 \(\sum\limits_{a}a\times dp_{n-1,a,1}\)。
最后来设计转移时的容斥系数。会发现如果第一棵树的非叶结点集合大小为 \(x\),第二棵树的非叶结点集合大小为 \(y\),则它对答案的容斥系数是 \((-2)^{n-x-y}\),相当于每个剩下的点都可以有两种选择——进入第一棵树或者进入第二棵树。所以只要在进行既不选入第一棵树,也不选入第二棵树的决策时乘上 \(-2\) 就可以了。转移方程就是
时间复杂度 \(O(n^3)\)。
另外官方题解是什么神仙东西。
ZJOI2022 Day1T2
tag:根号分治
引用题解里的一句话:一般 “出现次数” 都与根号分治挂钩,因为出现次数少的数可以直接考虑出现次数,出现次数多的数可以直接考虑每个数,这样就出现了根号。
这就作为这道题的突破口。设定阈值 \(B\),把出现次数大于 \(B\) 的数称为大数,出现次数小于等于 \(B\) 的数称为小数。原问题显然可以转化成:对所有区间 \([l,r]\),求区间内众数出现次数与区间外众数出现次数和的最大值,以及此时所有可能的区间外众数。
根号分治一般要找到两个暴力。第一个暴力是相对明显的:固定两个众数之一,\(O(n)\) 求出每个前缀中这个数的出现次数,枚举另一个数。显然区间的端点只会在另一个数的位置附近(\(\pm 1\)),然后对一个区间,它对答案的贡献的式子关于左右端点独立。因此只用维护一个前缀最大值。
这是考虑每个数的情形,所以应该对大数应用这个暴力,这一步的时间复杂度是 \(O(\frac{n^2}{B})\)。剩下的情况是内外众数都是小数的情况。
这时我们需要应用“众数出现次数不超过 \(B\)”的性质。考虑对每个左端点,求出最小的右端点,使得这个区间内的众数出现次数为 \(x\)。这个问题可以双指针做,对所有 \(x=1,2,\cdots,B\) 做一遍的复杂度就是 \(O(nB)\)。然后对于每个小数,枚举它作为区间外众数的情况,此时的区间的端点一定在这个数值附近。利用刚刚处理出来的东西更新答案即可。精细实现也可以做到 \(O(nB)\)。
取块长 \(B=\sqrt n\),理论复杂度 \(O(n\sqrt n)\)。实测 \(B=\frac{\sqrt n}{2}\) 跑的更快。
ZJOI2022 Day1T3
tag:图论,圆方树
首先对题目给出的性质做一些分析。显然这个性质对点双独立,手玩一下点双的情况会发现每个点双似乎只能是两点间连若干条链的形态(形如纺锤体)。事实上的确如此。
那么对每个点双预处理出链的数目,链的总长以及每个点在点双里的位置,就可以 \(O(\log)\) 查询该点双内两点间路径数目及总长度(\(\log\) 来自离散化)。注意特判查询时两点有一个是“纺锤体”的端点的情形,剩下的分在同一条链上与不在同一条链上讨论即可。
然后肯定是在圆方树上考虑询问,会发现除了 LCA 处都是一个点和它的二级祖先之间的路径数,可以预处理出来。LCA 处可能需要一次单独的询问。这里可以直接预处理出根到每个点的情况,因为 \((\text{路径数目},\text{路径长度总和})\) 这个二元组是可减的。
代码比较长,但是没有用到什么数据结构。时间复杂度容易做到 \(O(n\log n)\)(视 \(n,m,q\) 同阶)。一点细节是要把边分到点双里,可以先建出圆方树,然后就容易判断了。
ZJOI2022 Day2T2
tag:组合计数
神仙题。考察了选手的想象力。
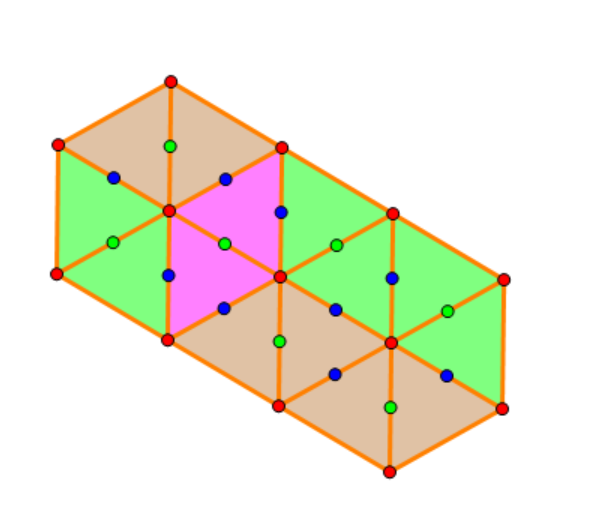
以样例的第一组数据为例,蓝色,绿色的点是可以选的点,绿色点是一种选择方式。如图构造出一些辅助线和图形,题目就可以看成是正方形堆叠。若记 \(a'=b+c-a,b'=c+a-b,c'=a+b-c\),会发现问题变成在 \(a'\times b'\) 的方格表上堆叠正方形,要求高度不超过 \(c'\),且从左往右,从上往下高度不增。那么标记出每个位置的高度 \(h_{i,j}\),要求 \(h_{i,j}\ge h_{i+1,j},h_{i,j+1}\)。发现这个东西很像杨表,记 \(h'_{i,j}=h_{i,j}+i\) 就可以转化成值域在 \([1,a'+c']\) 内的半标准杨表。用勾长公式计算方案数:(省略了 \(a',b',c'\) 的 \('\))
\(O(n)\) 预处理,\(O(1)\) 回答。至于点数也可以轻松得到,是 \(a'b'+b'c'+c'a'\)。当然有一点 corner case 就是 \(a',b',c'\) 有小于等于 \(0\) 的。不妨设为 \(a+b\le c\),此时整个图形(原来的点阵)近似一个平行四边形,容易得到点数是 \(4ab\),方案唯一。
ZJOI2020 Day1T2
tag:DP,矩阵乘法
首先显然把期望变成每个结点的概率。
对于一次修改 \([L,R]\),称完全包含在 \([L,R]\) 内的区间为 A 类,与 \([L,R]\) 没有交集的区间为 B 类,剩下的区间为 C 类(有交但不被包含)。考虑一次修改对一个线段树上区间的标记影响。如果这个区间是 C 类,它的标记会因为push_down消失;如果这个区间是 A 类,且它的父亲是 C 类,它会获得标记;如果这个区间是 B 类,且它的父亲是 C 类,则当它的祖先中有区间有标记时,它会获得标记。
那么我们发现还要考虑一个结点祖先的标记情况。当这个区间的父亲是 A 类时,它一定有一个祖先满足“本身是 A 类,父亲是 C 类(或没有父亲)”,所以祖先会得到标记;当这个区间的父亲是 B 类时,一定有一个祖先满足“本身是 B 类,父亲是 C 类”,所以祖先的标记情况不会改变;当这个区间的父亲是 C 类时,所有祖先都是 C 类,所以祖先会失去标记。
那么就可以定义状态:\(dp_{i,0/1,0/1}\) 表示进行了 \(i\) 次操作后,当前考虑的结点有/无标记,当前结点的祖先有/无标记的概率。设当前结点的区间为 \([l,r]\),父亲结点的区间为 \([l_0,r_0]\),考虑五种情况:
- 父亲是 A 类。情况数为 \(l_0(n-r_0+1)\)。除掉总情况数得到概率(下同),此时这个概率乘以 \(dp_{i,x,y}\rightarrow dp_{i+1,x,1}\)。
- 父亲是 B 类。情况数为 \(\frac{1}{2}(l_0(l_0-1)+(n-r_0)(n-r_0+1))\)。此时 \(dp_{i,x,y}\rightarrow dp_{i+1,x,y}\)。
- 父亲是 C 类,自身是 A 类。可以分 \(l_0=l\) 和 \(r_0=r\) 讨论,以前者为例,情况数为 \(l(r_0-r)\)。此时 \(dp_{i,x,y}\rightarrow dp_{i+1,1,0}\)。
- 父亲是 C 类,自身是 B 类。同样以 \(l_0=l\) 为例,情况数为 \(\frac{1}{2}(r_0-r)((n-r+1)+(n-r_0))\)。此时 \(dp_{i,x,y}\rightarrow dp_{i+1,x|y,0}\)。
- 父亲是 C 类,自身是 C 类。情况数为 \((r-l)(n-r+1)+\frac{1}{2}(l+r-1)(r-l)\)。此时 \(dp_{i,x,y}\rightarrow dp_{i,0,0}\)。
目标是 \(dp_{k,1,0}+dp_{k,1,1}\)。这个 DP 显然可以用矩阵优化。直接构建 \(4\times 4\) 的矩阵已经足以通过,复杂度 \(O(4^3n\log k)\)。实际上可以优化到 \(3\times 3\),把 \(dp_{\star,1,0}\) 和 \(dp_{\star,1,1}\) 加起来当作一个状态,仍然可以转移。
最后根结点可能需要特判一下,它的概率是区间数的倒数。
ZJOI2020 Day2T2
tag:DP,多项式
把期望变成概率,概率再变成方案数,来求有多少种取出 \(i\) 个数的方法是不合法的(没有连续 \(k\) 个数的)。取出第 \(i\) 个数的期望步数为 \(\frac{n}{i}\),因此若记这个数目为 \(cnt_i\),可以算出最终期望为 \(\sum \frac{cnt_i}{C_{n-1}^{i}}\)。
注意到每个连续段互不影响,所以可以分开来处理,最后使用分治 FFT 合并即可。令 \(f_{i,j}\) 表示考虑到(当前连续段)第 \(i\) 个数字,选择了 \(j\) 个数字的不合法方案数,则转移方程为 \(f_{i,j}=f_{i-1,j-1}+f_{i-1,j}-f_{i-k-1,j-k}\)。特别的,可以认为 \(f_{-1,j}=[j=0]\),这样方便定义 \(f_{k,k}\)。
将 DP 刻画成生成函数的形式:\(F_i(x)=(1+x)F_{i-1}(x)-x^kF_{i-k-1}(x),F_{-1}(x)=1\)。仅凭这个式子不好递推,但是可以用组合意义:对 \(F_m\),枚举走了 \(i\) 次 \(k+1\),\(m-i(k+1)\) 次 \(1\),则有
减去后面的东西是因为从 \(-1\) 直接跳一步 \(x^k\) 是不合法的。\(G\) 的式子可以分治 FFT 计算,只要维护出 \(\sum_{i=L}^{R}x^{(i-L)k}(x+1)^{(R-i)(k+1)}C_{m-i(k+1)}^{i}\) 和 \((1+x)^{R-L+1}\) 即可。总的时间复杂度是 \(O(n\log^2n)\)。
ZJOI2019 Day1T1
tag:DP,DP套DP
首先有一个大致的思路:只要求出有多少个 \(k\) 元集合包含给定的集合,并且是胡牌的,就可以求出答案。然后考虑 DP,定义 \(dp_{i,j,\star}\) 表示已经考虑了前 \(i\) 种牌,已经选了 \(j\) 张,判定胡牌的状态为 \(\star\)。
至于内层的 \(\star\),不难想到用 DP of DP 处理,也就是我们再设计一个判定胡牌的 DP。因为顺子可能出现的后效性,所以需要记下前面两种牌留了多少,上一种牌留了多少,这两维的范围不会超过 \(2\)(否则直接构造刻子)。另外还要记是否留了对子。在这些条件下,记下面子的最大数目。枚举进行转移,转移是容易的。七个对子的情况单独记一下就好。
最后我们直接把整个状态记下来,包括所有 \(18\) 种状态的一个状态,这样转移就是唯一的了。预处理会发现状态数并不大,在 \(2000\) 左右,然后跑 DP 就完了。
ZJOI2019 Day1T2
tag:线段树,矩阵乘法
考虑所有时刻线段树的每个结点有多少个标记。为了转移,根据自身有无和祖先有无分成四类,和20年D1T2的套路一模一样,就可以转移了。方便起见仍然用矩阵维护。则线段树上的每个结点乘 \(5\) 个矩阵之一。前三种的总点数在 \(O(\log n)\) 级别,后两种是 \(O(\log n)\) 棵子树的并。可以借用线段树的结构打懒标记,然后就做完了。
ZJOI2019 Day2T2
tag:树上启发式合并,虚树
考虑把所有点对分成两类:具有祖先后代关系的和不具有这种关系的。
对于前者,我们直接把给出的 \(m\) 条路径拆成(一条或两条)从祖先到后代的链,然后在深度较大的点统计答案。那就只需要把链较浅端点的深度挂在链较深的端点上,然后查询每个点子树内的最小值。可以用树上启发式合并 set 解决,时间复杂度是两只 \(\log\),当然也可以用线段树或 ST 表之类的,这里可以少一个 \(\log\)(虽然并不是瓶颈)。
对于后者,覆盖这个点对的路径的 LCA 一定与这两点的 LCA 相同,所以把所有路径挂在 LCA 处。假设当前考虑 LCA 为 \(x\) 的情况。把在每条路径的一个端点处记录它的另一个端点,那么一个点对答案的贡献就是它子树内标记的点到 \(x\) 路径的并集大小。这个问题按照 dfs 序排序之后很容易解决,就是所有点到 \(x\) 的距离和减去相邻两点的 LCA 到 \(x\) 的距离和(而且正好不会把 \(x\) 算进去)。那可以用一个 set 维护,在插入的时候计算新产生的贡献。同样使用树上启发式合并就可以解决。注意这个部分每个点对被算了两次。
如果用倍增求 LCA,复杂度会来到三只 \(\log\),不太优秀。可以用 DFS 序求 LCA ,这样总复杂度就是 \(O(n\log^2n)\)。实际表现很不错勉强能排到 uoj 和 loj 最优解的第一页。
ZJOI2017 Day1T1
tag:DP
先考虑树上问题。可以认为要用若干条路径覆盖所有边,然后对于长度大于 \(1\) 的路径在两端点间连边即可。那么使用 DP,设 \(dp_i\) 表示 \(i\) 子树内的边加上它到父亲的边构成的图的方案数。转移时只要把一个点的所有邻边用某种方式连接起来,这可以预处理一个 \(f_i\) 表示 \(i\) 条边的方案数。有 \(f_i=f_{i-1}+(i-2)f_{i-2},dp_u=f_{deg_u}\prod dp_v\)。一般问题,首先判断原图是否是仙人掌。然后找出所有的环,可以直接删掉,因为环上的边不能再被覆盖。那就变成了多棵树,直接方案数相乘即可。
ZJOI2017 Day1T2
tag:树套树
熟知发现题目中求了后缀和,那么正确的概率就是 \(a_{l-1}=a_r\) 的概率。考虑一个修改操作 \([l,r]\) 对 \(a_x-a_y\) 的影响。如果 \(x,y\) 都在区间内,则有 \(\frac{2}{r-l+1}\) 的概率变化;如果恰有一个在区间内,则有 \(\frac{1}{r-l+1}\) 的概率变化。
假设每一步分别有 \(a_1,a_2,\cdots,a_k\) 的概率变化,要求变化偶数次的概率。设 \(f(x)=\prod ((1-a_i)-a_ix)\),会发现偶数次的概率就是 \(\frac{1}{2}(f(1)+f(-1))\)。而 \(f(-1)=1\),所以只用求 \(f(1)\)。问题就可以刻画成:在二维平面上,每次给一个矩形内的点乘以 \(x\),询问单点值。这只要用树套树维护即可。
注意要特判 \(l=1\) 的情况。
ZJOI2017 Day2T2
tag:树状数组,倍增
将答案分为三部分:\(S_{[l,r]}\) 内所有点的深度和,加上 \(S_{[l,r]}\) 内的点数乘以 \(u\) 的深度,再减去所有 LCA 的深度和的两倍。
第一部分,对每个叶子结点,赋权值 \(d\);对非叶子结点,赋权值 \(-d-2\),这里 \(d\) 是深度。会发现只要求出询问区间 \([x,y]\) 内的所有结点权值之和就得到答案。这可以离线二维数点。第二部分也类似,对叶子结点赋权值 \(1\),非叶子结点赋权值 \(-1\) 即可。
第三部分,会发现所有 LCA 的深度和就是 \(u\) 的所有祖先(根结点除外)子树内在 \(S_{[x,y]}\) 内的数目的和。考虑从一个结点 \(a\) 到它的父亲结点 \(b\) ,这个数目变化了多少。发现如果 \(a,b\) 和询问区间 \([x,y]\) 都处于相交的状态,那么答案一定增加 \(0\) 或 \(1\),取决于变化的边界是否在 \([x,y]\) 内。所以可以考虑倍增,求出第一个“包含 \([x,y]\) 的祖先结点”和第一个 “与 \([x,y]\) 有交但不被包含的结点”,除去在中间部分增加的贡献,就是询问这两个区间内部包含 \(S_{[x,y]}\) 内结点的数目,同样使用上面的方法,进行离线二维数点;中间部分增加的贡献可以用矩阵来刻画,进一步优化会发现只用记录矩阵里的三个值,倍增维护即可。
总时间复杂度 \(O(n\log n)\)。
ZJOI2016 Day1T2
tag:分治,最短路
直接考虑对矩形分治。把长边切开,求出中间一列到所有点的距离,更新所有询问的答案,然后把两侧的询问递归下去。可以算出时间复杂度是 \(O(S\sqrt S\log S)\) 的。
ZJOI2016 Day1T3
tag:DP,容斥原理
会发现“排列”的限制,也就是要求互不相同的限制难以处理。所以考虑容斥。给树上每个结点赋一个集合 \(S\) 中的编号,只要求树上相邻的两个编号在图中也相邻,不要求互不相同。这可以直接在树上 DP 求解方案数,复杂度 \(O(n^3)\)。容斥枚举 \(S\) 即可。时间复杂度 \(O(n^32^n)\)。
ZJOI2016 Day2T2
tag:DP
先考虑一个朴素的 DP。固定一个值 \(x\),设 \(dp_{x,i,l,r}\) 表示 \(i\) 次操作后区间 \([l,r]\) 是一个小于 \(x\) 的极长段的方案数。转移是容易的。令 \(x=val_j\),\(val\) 是离散化数组,求出 \(f_{j,i}=\sum_{i\in[l,r]}dp_{x,q,l,r}\),则最终位置 \(i\) 值为 \(val_j\) 的方案数是 \(f(j,i)-f(j-1,i)\)。然后会发现一个 \(f(j,i)\) 的贡献系数是 \(val_j-val_{j+1}\),于是直接把这个贡献丢到 DP 里面,即设 \(g_{i,l,r}=\sum dp_{val_j,q,l,r}(val_j-val_{j+1})\),转移不变。前缀和优化转移,复杂度就变成了 \(O(n^2q)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号