CF1753D 题解

因为最后要找的是“腾出空位”的最小代价。

所以不妨把“障碍的移动”转化为“空位的移动”。

令 \(f_{x,y}\) 为：使得 \((x,y)\) 为空，至少需要多少代价。

下面来找转移方程，显然转移方程与空格子移动有关。所以观察空格子移动的规律。

若当前格子 \((x,y)\) 为 L。

• 以 \((x,y+1)\) 为顶点顺时针或逆时针旋转当前障碍，就可以使 \((x,y)\) 格子变为空。

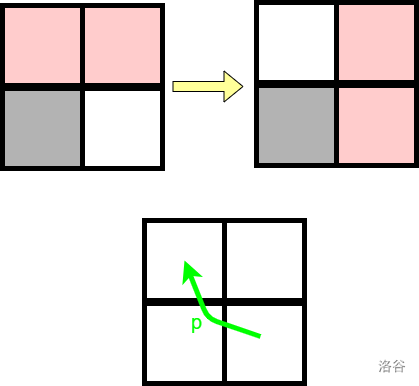
上图中，粉色格子为当前障碍，白色格子为空。如果按逆时针旋转90度，粉色障碍就会发生如上的变化，那么右下角的空格子就会移动到左上角。所以从有 \(f_{x,y}=f_{x+1,y+1}+p\)。同理，如果按顺时针旋转90度，\((x+1,y-1)\) 的空格子可以移动到 \((x,y)\)（读者不妨在草稿本上自己画一下图）。所以有 \(f_{x,y}=f_{x+1,y-1}+p\)。

• 如果把当前障碍整体向右平移一格，那么 \((x,y+2)\) 的格子可以移动到 \((x,y)\)，所以有式子 \(f_{x,y}=f_{x,y+2}+q\)。

现在把三个式子合并起来，取最小值，就是 \(f_{x,y}=\min(f_{x+1,y-1}+p,f_{x+1,y+1}+p,f_{x,y+2})\)。我们现在就已经得到了当前格子为 L 的转移。

另外三种障碍的情况也差不多，画一画图就能写出式子。注意 # 的情况设为 \(inf\)，. 的情况设为 \(0\).

---

好了我们已经 DP 式子了，但是怎我们找不到一个合适的顺序取遍历所有格子呀？一个常见的 trick 是把 DP 转化成图论问题。

如果有 \(f_{x,y}=f_{x',y'}+v\)。那么就从 \((x',y')\) 向 \((x,y)\) 连一条值为 \(v\) 的边，最后在整个图上跑最短路就可以了。

一个小细节，在实现代码时可以建立虚拟源点 \(s\)。如果我们把 \(f_{x,y}\) 设为 \(0\)，就从 \(s\) 向 \((x,y)\) 连接一条值为 \(0\) 的边。

Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=3e5+5;
int n,m,p,q;
struct node{int to;ll w;};
bool operator <(const node &x,const node &y){return x.w>y.w;}
vector<node> G[MAXN];
ll dis[MAXN];
bool vis[MAXN];
void dij(){
    priority_queue<node> q;
    q.push({0,0});
    memset(dis,0x3f,sizeof(dis));
    dis[0]=0;
    while(!q.empty()){
        int u=q.top().to;q.pop();
        if(vis[u])  continue;
        vis[u]=1;
        for(node t:G[u]){
            int v=t.to;
            if(dis[v]>dis[u]+t.w){
                dis[v]=dis[u]+t.w;
                q.push({v,dis[v]});
            }
        }
    }
}
int dir[8][2]={{0,1},{0,-1},{1,0},{-1,0}};
const ll INF=0x3f3f3f3f3f3f3f3f;
int main(){
    #ifndef ONLINE_JUDGE
        freopen(".in","r",stdin);
        freopen(".out","w",stdout);
    #endif
    scanf("%d%d%d%d\n",&n,&m,&p,&q);
    vector<string> mp(n);
    for(int i=0;i<n;i++)   cin>>mp[i];
    auto get=[&](int x,int y)->int {return x*m+y+1;};
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            
            auto link=[&](int x,int y,int w)->void {
                if(x<0||y<0||x>=n||y>=m)    return;
                G[get(x,y)].push_back({get(i,j),1ll*w});
                // cerr<<get(i,j)<<" "<<get(x,y)<<" "<<w<<endl;
            };

            if(mp[i][j]=='L')   link(i-1,j+1,p),link(i+1,j+1,p),link(i,j+2,q);
            if(mp[i][j]=='R')   link(i-1,j-1,p),link(i+1,j-1,p),link(i,j-2,q);
            if(mp[i][j]=='U')   link(i+1,j-1,p),link(i+1,j+1,p),link(i+2,j,q);
            if(mp[i][j]=='D')   link(i-1,j-1,p),link(i-1,j+1,p),link(i-2,j,q);
            if(mp[i][j]=='.')   G[0].push_back({get(i,j),0});
        }
    }
    dij();
    ll ans=INF;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            for(int k=0;k<4;k++){
                int di=i+dir[k][0],dj=j+dir[k][1];
                if(di<0||di>=n||dj<0||dj>=m)    continue;
                ans=min(ans,dis[get(i,j)]+dis[get(di,dj)]);
            }
        }
    }
    if(ans==INF)    ans=-1;
    printf("%lld",ans);
    return 0;
}