LCA性质

参考博客

1

\[LCA(p_1,p_2,p_3...p_n)=LCA(LCA(LCA(p_1,p_2),p_3),...p_n) \]

证明略

2

\[LCA(p_1,p_1,p_2)=LCA(p_1,p_2) \]

所以LCA相关可以用ST表维护。

3

若 \(\{p_n\}\) 为树的一个DFS序，则

\[LCA(p_l,...p_r)=LCA(p_l,p_r) \]

证明：

考虑归纳证明。假设 \(LCA(p_l,...p_{r-1})=LCA(p_l,p_{r-1})\) 成立，考虑证明 \(LCA(p_l,...p_r)=LCA(p_l,p_r)\)

\(LCA(p_l,...p_r)=LCA(LCA(p_l,...p_{r-1}),p_r)=LCA(LCA(p_l,p_{r-1}),p_r)\)

即证：\(LCA(LCA(p_l,p_{r-1}),p_r)=LCA(p_l,p_r)\)

设 \(l=LCA(p_l,p_{r-1})\).

需要证明 \(LCA(p_l,p_r)\) 是 \(l\) 和 \(p_r\) 的祖先（下面称为合法的），且是不能再往下移动（下面称为最优的）。（意思就是找出来的LCA是最深的）

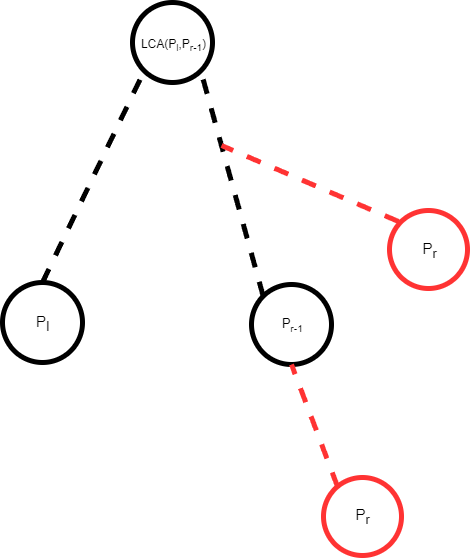
1. 若 \(p_r\) 在 \(l\) 子树内。那么显然是合法的。为什么是最优的？因为根据dfn序的性质，如果 \(LCA\) 还能往下移动，说明 \(p_r\) 的DFN序比 \(p_{r-1}\) 更小。但是 \(dfn_{p_r} > dfn_{p_{r-1}}\)

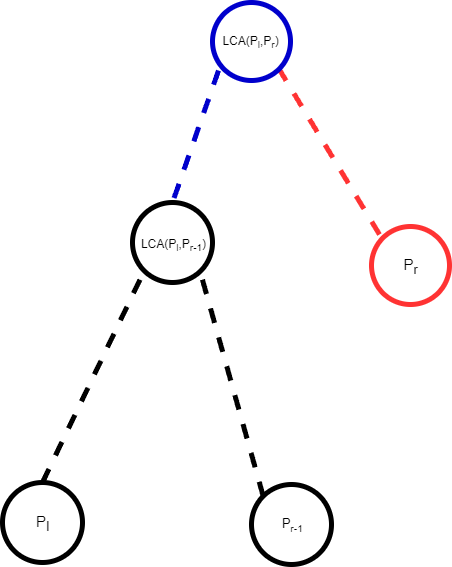
2. 若 \(p_r\) 不在 \(l\) 子树内。合法性：\(LCA(p_l,p_r)\) 必定在 \(p_l\) 到根的路径上， \(l\) 也在 \(p_l\) 到根的路径上，且肯定深度大于 \(LCA(p_l,p_r)\)，所以 \(LCA(p_l,p_r)\) 为 \(l\) 和 \(p_r\) 的公共祖先。最优性： 略。

4

若 \(\{p_n\}\) 为树的一个DFS序，则 对于给定的 \(i\)，随着 \(j\) 增大，\(dep[LCA(p_i,p_j)]\) 非严格递减。

另一种说法：对于给定的 \(u\)，\(v\) 在 \(DFS\) 序上越靠近 \(u\) , \(dep[LCA(u,v)]\) 越大。

证明：

其实画个图就很好理解了。具体的数学证明运用性质 \(3\) 。

\(dep[LCA(p_i,p_j)]\)

\(=dep[LCA(p_i,...,p_j)]\)

\(=dep[LCA(LCA(p_i,...,p_{j-1}),p_j)]\)

\(\leq dep[LCA(p_i,...p_{j-1})]\)

5

若 \(\{ p_n \}\) 为树的一个排列。

\(LCA(p_l,...p_r)\) 就是 \(LCA(p_i,p_{i+1})\) 中深度最小的 \(LCA\).

当然也有下面的结论：

\[dep[LCA(p_l,...p_r)]=\min _{i=l}^{i<r}(dep[LCA(p_i,p_{i+1})]) \]

证明

大概思路，设 \(l=LCA(p_l,...p_r)\).那么一定存在一个 \(i\)，满足 \(p_i\) 和 \(p_{i+1}\) 不在 \(l\) 的同一个儿子的子树内。这时，\(l=LCA(p_i,p_{i+1})\)

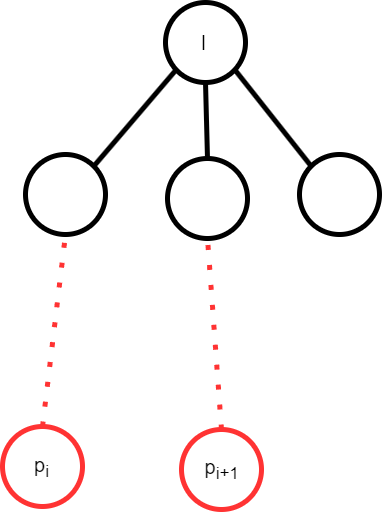
更详细的证明请看 参考博客