模拟赛（1~10）

一、高一高二联合模拟赛一

T1:灰烬十字

根据 $n$ 的范围，容易想到$dp$.因为“同一斜线上”的象会互相攻击，所以不妨将矩阵旋转90°。下文的行和列指旋转后的行、列。发现奇偶性相同的列会互相攻击。所以把奇数列，偶数列分开讨论。以奇数列举例，因为他们的长度先增加后减少，不好进行转移。所以关于中心两列对称的两列要一起考虑。定义 $dp_{i,j}$ 为长度前 $i$ 小的列中，总共放了 $j$ 个的方案数。每一列最多只能放一个，所以对于“一对列”来说，只有两个情况，取一个或取两个。

如图，红色列和蓝色列不会相互影响，红色列和红色列之间会相互影响。蓝色列和蓝色列之间会相互影响。

当计算蓝色列时，$dp_{i,j}$ 为前 $i$ 列，和后 $i$ 列中，总共放了 $j$ 个的方案数。

T2:斗鸡

区间问题，先排序看性质。先按左端点从左到右排序，右端点暂时不清楚怎么排。先不考虑左端点重合的情况。“恰好”有 $m$ 个区间满足要求。那么思考怎么涂色能确定 这种方案会影响多少个区间。因为左端点不同，所以在最左边放两个 $1$,后面的区间不会被这两个 $1$ 影响。前面的区间，若右端点大于第二个$1$ ，则会被影响。如果一个一个判断太麻烦，不妨把前面所有的区间都变成满足条件的。所以方案就是，对前 $m$ 个区间，在其最左边放两个$1$。但是这是左端点不同的情况。有相同左端点怎么办？若当前区间为 $[l,r]$，还是对$a_l,a_{l+1}$ 赋值为$1$。那么所有左端点为 $l$ 的区间都会成为满足条件的区间。可以计算出左端点为 $l$ 的区间个数 $cnt$.如果“左端点小于 $l$ 的，满足条件的” 区间数量 $sum$ 加上 $cnt$ 小于$m$.直接把$a_l,a_{l+1}$ 赋值为 $1$ 就可以了，$sum+=cnt$。但如果不能全部都加到“满足条件的区间”。那该怎么办？此时按照右端点从大到小排序，设最后一个能加到$m$ 个”满足条件区间"的区间为 $x$。把 $x$ 的右端点赋值为 $1$，就可以使所有与 $x$ 左端点相同的，右端点大于 $r_x$ 的区间满足条件。因为这是最后一个满足条件的区间了，所以不用考虑 $r_x$ 为 $1$ 对后面区间的影响。最后，对每个没有被赋值为 $1$ 的点，赋值不同的值就好了。

T3:

T4：

二、高一高二联合模拟赛二

T1: 英雄 \

要找 $[l,r]$ 的最小公倍数的 $0$ 的个数。将 $x$ 分解为$2^{c2} \times 3^{c3} \times 5^{c5} \times ...$。$0$ 的个数等于 $\min(c2,c5)$ ，而 $c2$ 取决于 $[l,r]$ 中最大的 $c2$. $c5$ 取决于 $[l,r]$ 中最大的 $c5$.所以直接枚举$c2$。若在 $[l,r]$ 中有 $2^{c2}$ 的倍数，则 $c2$ 满足题意。$c5$ 同理。

T2: 卢娜

下文的合并即指合并后去除。

答案分成两部分：合并的部分（$n/2$），交换的部分。

要具体地知道怎么交换很难。但是每一对相同的数，设为$a_l,a_r$，有一个简单的贪心：$[l,r]$ 中如果出现了相同的数，那么一定先合并那一对。所以要让$a_l,a_r$合并，代价为 $[l,r]$ 中只出现一次的数的个数。用树状数组维护。

感觉很妙，从单个点的角度计算了对答案的贡献。想这种求最优方案的题，可以用$dp$(很常见)，构造（如T1），还有就是这个题的做法。

T3:

T4

三、高一高二联合模拟赛三

T1. 切蛋糕 \

注意到 $n,m$ 都很小，所以暴力搜索横着怎么切 $O(2^{14})$。然后题目就变成了，怎么竖着切，让最小值最大。就变成了经典二分问题。区别是从一维变成了二维，但是预处理一下同一列上，某一区间内的最小值就可以了。

T2. 羊了个羊

T3. 彩树

T4. 剪刀石头布

四、高一高二联合NOIP模拟赛4

T1:

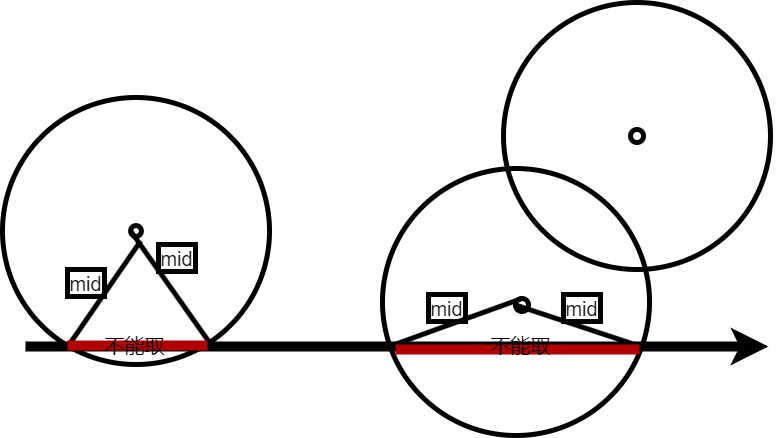
求线段上的点离最近的点最远的距离，显然二分。下文中，要在线段上选的点为 $x$。设二分值为 $mid$.那么所有点到 $x$ 的距离大于等于 $mid$。又因为，我们知道每个点的纵坐标，就可以算出在线段上的某一个不能取的区间（见下图）。所以只需要判断线段上是否有可以取的位置就可以了。但是这个地方有一个优化，我在考场上打的做法是，求出每个点对应的不能取的区间并按左端点排序，然后遍历区间并判断。其实可以在二分外提前排序，因为每个点对应的区间可以转化为半径为$mid$的圆与线段的交点。每个点对应的圆大小相同但位置不同，而位置只取决与圆心。显然圆心就是点。点在二分之前就已经固定了。

T2:

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int T;
int n,m;
typedef long long ll;
const int MAXN=2e5+5;
struct node{
	ll x,y;
}a[MAXN],b[MAXN];
bool cmp1(node p,node q){return p.x<q.x;}
bool cmp2(node p,node q){return p.x>q.x;}
int main(){
    // freopen("1.in","r",stdin);
// 	scanf("%d",&T);
    T=1;
	while(T--){
		scanf("%d",&n);
		for(int i=1;i<=n;i++)
			scanf("%lld%lld",&a[i].x,&a[i].y);
        scanf("%d",&m);
        ll tot=0;
        for(int i=1;i<=m;i++){
            scanf("%lld%lld",&b[i].x,&b[i].y);
            tot+=b[i].y;
        }
        sort(a+1,a+1+n,cmp2);
        sort(b+1,b+1+m,cmp1);
        ll cnt1=0,cnt2=0;//有多少行，多少列
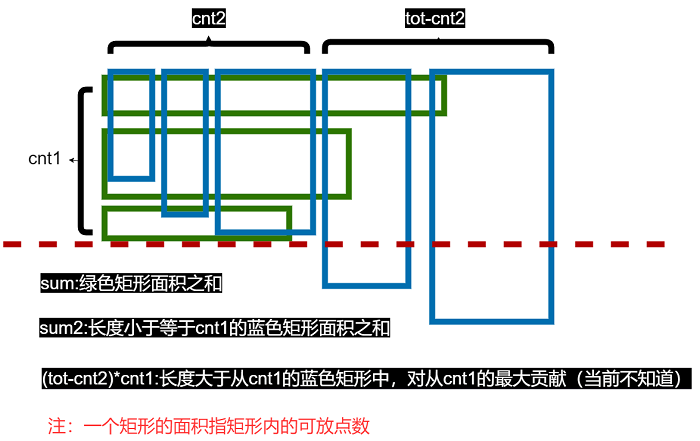
        ll sum1=0,sum2=0;//有多少个点
        bool flag=1;
        int j=1;
        for(int i=1;i<=n;i++){
            cnt1+=a[i].y;
            sum1+=a[i].x*a[i].y;
            while(j<=m&&b[j].x<=cnt1){
                cnt2+=b[j].y;
                sum2+=b[j].x*b[j].y;
                j++;
            }
            if(sum1>sum2+(tot-cnt2)*cnt1){
                flag=0;
                break;
            }
        }
        printf("%d\n",flag);
	}
    return 0;
}

五、高一联合NOIP模拟赛5

T1.失落的世界

容易想到的50分做法：还是二分找数，设当前值为mid，上一次询问为las。在las+mid和las-mid中选一个合法的数查询，如果两个数都不合法，就先询问一次1，再询问mid+1.最多会询问$2\log n$次。

考虑怎么减少“询问1”的次数。发现产生不合法是因为之前在las+mid和las-mid都合法时，无法判断选哪一个，所以随便选了一个。所以倒着求一遍答案，假定x=n（可以证明每次选右半部分能成立的话，选左半部分也能成立）。

T2.谜域的界外\

容易发现：1.碎片的数量很小 2.从左到右，碎片的从坐标递增，可以视为一条上升的斜线。

若初始位置在斜线上，会发现，最优的方案是先沿着斜线向上走一段，把这一段上的点收集了，如果时间还允许，就再向下返回到起点，再继续往下走。

若初始位置不在起点上，最优的方案是从初始位置先走到斜线上的某一点，然后就和第一种情况一样了。

T3.聚合的塔尖

注意到：$\sum k \le 1e5$，考虑根号分治设 $B=\sqrt n$

先预处理出，对于每个点 $u$，能到达 $u$ 的距离前 $B$ 小的碎片。（建反图，合并时双指针维护）

如果当前的 $k \ge B$.这样的 $k$ 不会超过 $\sqrt n$ 个.就直接暴力标记那些点不能走，然后 $O(n)$ DP；

如果当前的 $k \le B$.直接用预处理的值，找到最小的合法的点就可以了。

T4:沉眠的回声

六、高一高二联合NOIP模拟赛6

T1.糗大了

删除点可能有点抽象（但是可做的，并查集删点）。转化成加点。答案反着存就可以了。

警告：longlong！

T2. 快哭了

摘录的题解，有一些补充

考虑在 $k$次 $f$ 操作后，原数组中位置 $(i,j)$ 对答案的贡献，$(^{k}_{i})\times(^{k}_{j})$次（把$(i,j)$想象成二维坐标系中的点，他要走到 $(0,0)$）。由于是异或操作，所以只有在贡献次数为奇数时才有实际的贡献。根据Lucas定理，$(^{k}_{i})\times(^{k}_{j})$为奇数等价于 $k i=i$，$k \land j=j$ （按位与），即 $(k \land (i \lor j))=(i \lor j)$（按位或），这个东西不就很像前缀和了吗。那么真正需要考虑的 $k$ 就是 $max(n,m)$ 在二进制下最高位以内的数位。也就是只需要预处理出 $0 \le k \le 2^{23}$的答案。使用高维前缀和优化即可。时间复杂度$O(max(n, m)\log max(n, m) +q)$。

T3.色 (se)

还没调出来\流汗

T4.发怒

摘录题解：

考虑点分治，每次求出在当前处理的这个连通块中，包含分治中心且符合条件的方案数。求出以分治中心为根的dfs序，考虑$f(i,j)$表示考虑了dfs序中的前 $i$ 项，目前点集内乘积为 $j$ 的方案数。注意到状态里记录乘积恰好为 $j$ 很浪费，可以记录最大还能乘到多少，即 $f(i,\lfloor {m \over j}\rfloor)$ 表示考虑了dfs序中的前 $i$ 项，目前点集内乘积为$j$ 的方案数，这样第二维就只有 $O(\sqrt m)$ 种取值。转移的话，每次在递归的时候将这个点的方案传给儿子，再在回溯的时候将儿子的贡献加回父亲上即可。总的时间复杂度 $ O(n\sqrt m \log n)$。

有两个trick:

点分治对联通块计数
记录整数的乘积的值时，而乘积较大时，分为两部分，若当前值$w \le sqrt(V)$，直接记录；否则在另外的数组里记录 $\lfloor {V \over w}\rfloor$

七、高一高二联合NOIP模拟赛7

T1.大梦的曲调

单独写了一篇题解

T2.方碑解密（decrypt）

每一段操作对应一个 cnt 数组，判断某一子段是否等价于原段，判断 cnt 数组是否相等即可。暴力判断数组相等是 $O(len)$，$len$ 为数组长度，考虑优化，用哈希维护数组。

用哈希维护后，要询问子段，就转化成了前缀和。表示子段 $[l,r]$ 的 cnt 可以用 $[1,r]$ 的哈希值和 $[1,l-1]$ 的哈希值来表示。两个问题：1.怎么维护前缀 2.怎么用前缀表示区间

考虑求前 $[1,i]$ 次操作对应的哈希值 $S_i$.若 $a_i=$ "<"或">"，$S_i=S_{i-1}$，位置改变。若$a_i=$ "+"或"-"，$S_i$ 在 $S_{i-1}$ 的基础上加上当前位置 $x$ 对应的值，位置不变。
用前缀表示区间：不能直接 $S_r-S_{l-1}$.因为在 $[1,l-1]$ 之间的位移不应该对 $[l,r]$ 区间的哈希值产生影响，但$S_r-S_{l-1}$ 是算了 $[1,l-1]$ 之间的位移的影响的，所以要消掉，想象一下，为了消除影响，整个 cnt 数组会整体平移一段区间，方向与 $[1,l]$ 区间中的移动方向相反，大小与 $[1,l]$ 区间中的移动大小相同。怎么用哈希表示呢？二进制的位移可以用乘法或除法表示，显然这里也可以。具体的式子看代码。

预处理前缀和，枚举区间右端点 $r$，设左端点为 $l$，可以列出一个有 $S_r, S_l,S_n$ 的方程， $S_r,S_n$ 已知，所以可以求出 $S_l$ 所以找 $[1,r]$ 中有多少个 $S_l$ 即可，用map存一下。

细节：双哈希。

King

八、高一高二联合NOIP模拟赛8

T1.学飞机

最优策略，贪心

若 $k=1$，很简单的贪心：每一次将所有能学的模块都学了，知道所有模块都学完。（学习模块的顺序其实没有影响）

$k \neq 1$，瓶颈在于如何判断当前能学的模块有那些。一个模块有 $k$ 个性质，因为我们只关心k个性质有没有全部满足，而不在乎哪些满足。用类似拓扑排序的思路，维护 cnt[i] 表示 i 模块有多少个性质还没有被满足。若 cnt[i]=0 就可学。i 可学后，更新 k 个性质。因为每个 i 只会更新性质 1 次。所以时间复杂度为 $O(nk)$

T2.造飞机

暴力，

T3.开飞机

最优策略，分析性质

一个性质是：在上升过程中，不上升一定不会优于上升。在下降过程中，不下降一定不会优于下降。所以我们大概的路线就是先从起点一直上升到某个点 x，再从 x 平移一段到 y，再从y下降到n（在上升和下降过程中，一个时间会上下移动一个单位，所以也要求起点到x与x到n的时间一样）。又发现，把中间平移的一段换为上升后再下降，答案也是一样的，这样做的好处就是省去了枚举 y 的时间。但是当 x 到 y 的距离为奇数时，中间必定有一段平移（因为要求上升和下降的时间平分）。枚举 x 的相邻结点 y 即可。

T4.隐身飞机

九、高一高二联合NOIP模拟赛9

T1.早操\

最优策略，找性质。

遇到这种整个数组中只有两种值的情况（这道题是 L 和 R）。一般可以考虑把一段连续的相同的值划分为同一段，整个数组也就被划分为若干段。

T2.采购

最优策略