欧拉函数

一、 定义

\(\varphi (x)\) 表示的是小于等于 \(n\) 和 \(n\) 互质的数的个数。

二、 特殊值

\(\varphi (1)=1\)

当\(x\)为质数时，\(\varphi (x)=x-1\)。

三、性质

1. 欧拉函数是积性函数。 即\(\varphi (x \times y)= \varphi(x)\times\varphi(y)\)，\(\gcd ({a},{b})=1\)

2. 若 \(n=p^k\)，\(p\) 为质数，\(\varphi (n)=p^k-p^{k-1}\)

四、求解

分解出 \(n=x1^{k1}x2^{k2}...xm^{km}\)

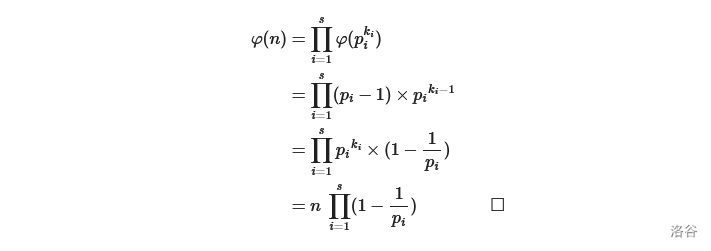
所以求欧拉函数的关键在于求它的质因子。

方法一：朴素算法

直接分解质因数

ll euler_phi (ll x) {
	ll ans = x;
	for (int i = 2; i * i <= x; i++) {
		if (x % i == 0)	ans = ans - ans / i;
		while (x % i == 0)	x /= i;
	}
	if (x > 1)	ans = ans - ans / x;
	return ans;
}

方法二：用欧拉筛求欧拉函数

在欧拉筛的时候可以得到每个数的最小质因子。

const int N = 100005;
typedef long long ll;
int T, n;
bool f[N];
int p[N], tot;
ll phi[N], s[N];
void pre () {
	f[1] = f[0] = 1;
	phi[1] = 1;
	for (int i = 2; i <= N; i++) {
		if (!f[i])	p[++tot] = i, phi[i] = i - 1;
		for (int j = 1; j <= tot && p[j] * i <= N; j++) {
			f[p[j]*i] = 1;
			if (i % p[j] == 0) {//k1>1
				phi[p[j]*i] = (ll)p[j] * phi[i]; 
				break;
			} else phi[p[j]*i] = (ll)(p[j] - 1) * phi[i];
		}
	}
}