Loading

Map集合、散列表、红黑树介绍

一、Map介绍

Map与Collection的区别

Map集合的特点：

  • 将键映射到值的对象，一个映射不能包含重复的键，每个键最多只能映射到一个值

Map和Collection集合的区别：

  • Map集合存储的元素时成对出现的，Map的键时唯一的，值时可以重复的
  • Collection集合存储的元素时单独出现的，Collection的儿子Set时唯一的，List时可重复的

要点：

  • Map集合的数据结构针对键有效，和值无关
  • Collection集合的数据结构针对元素无效

 

Map的功能

下面我们来看Map的源码

image.png

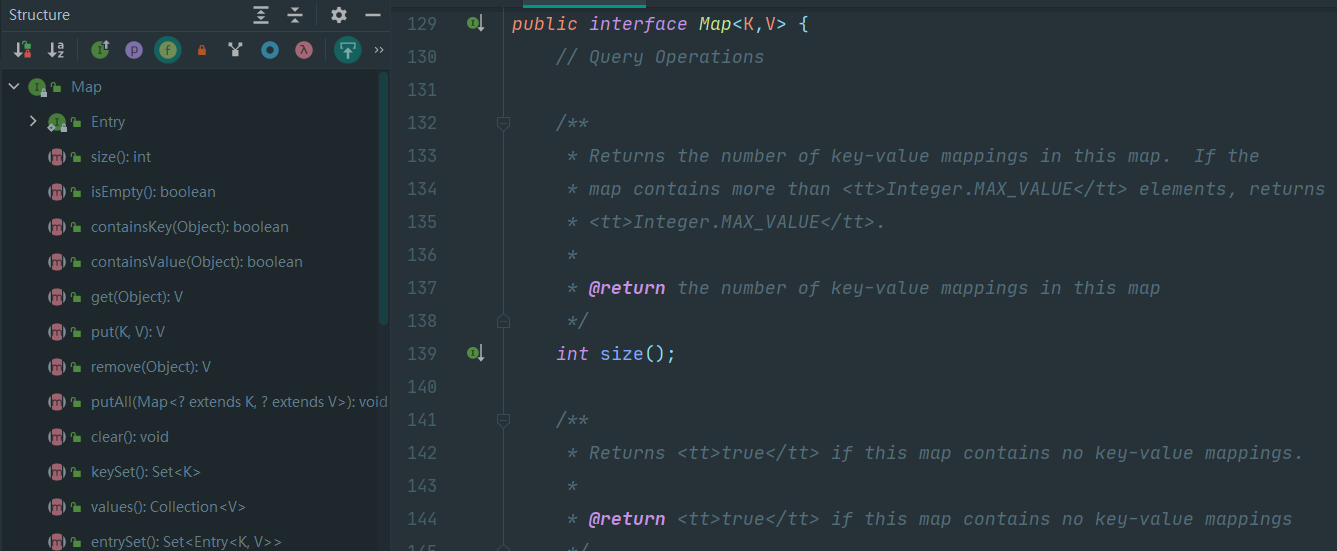
常用的Map方法

image.png

Map的子类结构

image.png

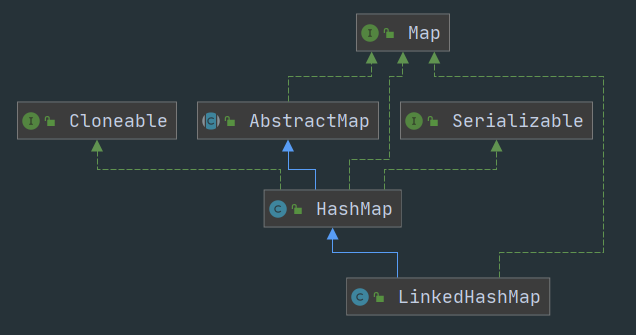
二、散列表介绍

无论是Set还是Map，我们会发现都会有对应的-->HashSet,HashMap

首先我们也先得回顾一下数据和链表：

  • 链表和数组都可以按照人们的意愿来排列元素的次序，他们可以说是有序的(存储的顺序和取出的顺序是一致的)
  • 但同时，这会带来缺点：想要获取某个元素，就要访问所有的元素，直到找到为止。
  • 这会让我们消耗很多的时间在里边，遍历访问元素~

而还有另外的一些存储结构：不在意元素的顺序，能够快速的查找元素的数据

  • 其中就有一种非常常见的：散列表

 

算散列表工作原理

散列表为每个对象计算出一个整数，称为散列码。根据这些计算出来的整数(散列码)保存在对应的位置上！

在Java中，散列表用的是链表数组实现的，每个列表称之为桶。

 

一个桶上可能会遇到被占用的情况(hashCode散列码相同，就存储在同一个位置上)，这种情况是无法避免的，这种现象称之为：散列冲突

  • 此时需要用该对象与桶上的对象进行比较，看看该对象是否存在桶子上了~如果存在，就不添加了，如果不存在则添加到桶子上
  • 当然了，如果hashcode函数设计得足够好，桶的数目也足够，这种比较是很少的~
  • 在JDK1.8中，桶满时会从链表变成平衡二叉树

如果散列表太满，是需要对散列表再散列，创建一个桶数更多的散列表，并将原有的元素插入到新表中，丢弃原来的表~

  • 装填因子(load factor)决定了何时对散列表再散列~
  • 装填因子默认为0.75，如果表中超过了75%的位置已经填入了元素，那么这个表就会用双倍的桶数自动进行再散列

 

三、红黑树介绍

上面散列表中已经提过了：如果桶数满的时候，JDK8是将链表转成红黑树的~。并且，我们的TreeSet、TreeMap底层都是红黑树来实现的。

所以，在这里学习一波红黑树到底是啥玩意。

 

各种常见树的用途

AVL树:最早的平衡二叉树之-。应用相对其他数据结构比较少。windows对进程地址空间的管理

用到了AVL树。

红黑树:平衡二叉树，广泛用在C+ +的STL中。如map和set都是用红黑树实现的。

B/B+树:用在磁盘文件组织数据索引|和数据库索引。

Trie树(字典树):用在统计和排序大量字符串,如自动机。

 

回顾二叉查找树

首先我们来回顾一下：利用二叉查找树的特性，我们一般来说可以很快地查找出对应的元素。

可是二叉查找树也有个例(最坏)的情况(线性)：

image.png

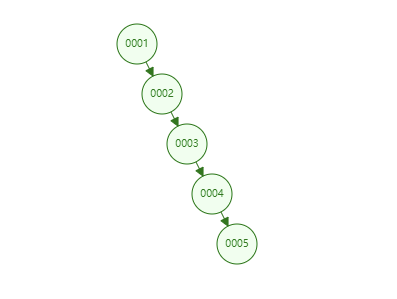
上面符合二叉树的特性，但是它是线性的，完全没树的用处~

树是要“均衡”才能将它的优点展示出来的~，比如下面这种：

image.png

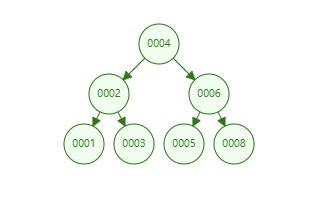
因此，就有了平衡树这么一个概念~红黑树就是一种平衡树，它可以保证二叉树基本符合矮矮胖胖(均衡)的结构

 

知新2-3树

讲到了平衡树就不得不说最基础的2-3树，2-3树长的是这个样子：

image.png

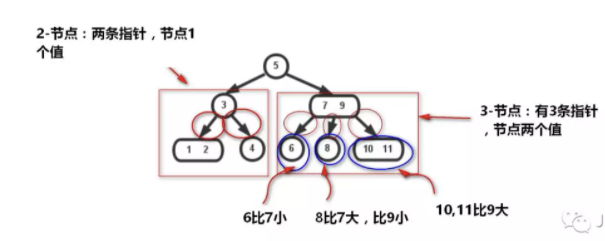
在二叉查找树上，我们插入节点的过程是这样的：小于节点值往右继续与左子节点比，大于则继续与右子节点比，直到某节点左或右子节点为空，把值插入进去。这样无法避免偏向问题

而2-3树不一样：它插入的时候可以保持树的平衡！

在2-3树插入的时可以简单总结为两个操作：

  • 合并2-节点为3-节点，扩充将3-节点扩充为一个4-节点
  • 分解4-节点为3-节点，节点3-节点为2-节点
  • ……..至使得树平衡~

合并分解的操作还是比较复杂的，要分好几种情况

 

红黑树

由于2-3树为了保持平衡性，在维护的时候是需要大量的节点交换的！这些变换在实际代码中是很复杂的，大佬们在2-3树的理论基础上发明了红黑树(2-3-4树也是同样的道理，只是2-3树是最简单的一种情况，所以我就不说2-3-4树了)。

  • 红黑树是对2-3查找树的改进，它能用一种统一的方式完成所有变换。

红黑树是一种平衡二叉树,因此它没有3-节点。那红黑树是怎么将3-节点来改进成全都是二叉树呢？

红黑树就字面上的意思，有红色的节点，有黑色的节点：

image.png

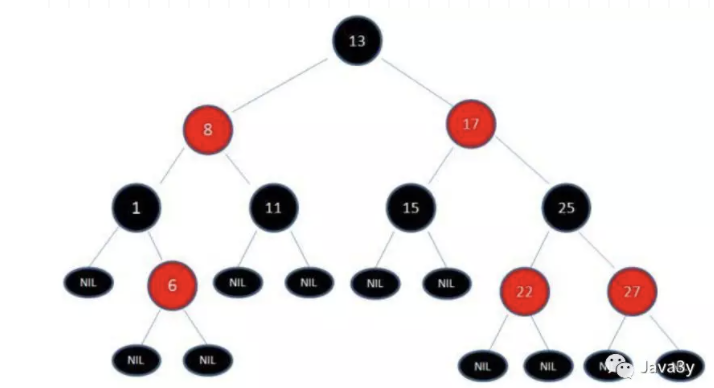
我们可以将红色节点的左链接画平看看：

image.png

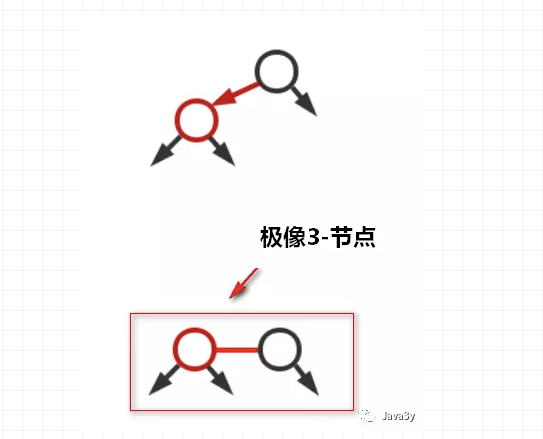
一颗典型的二叉树：

image.png

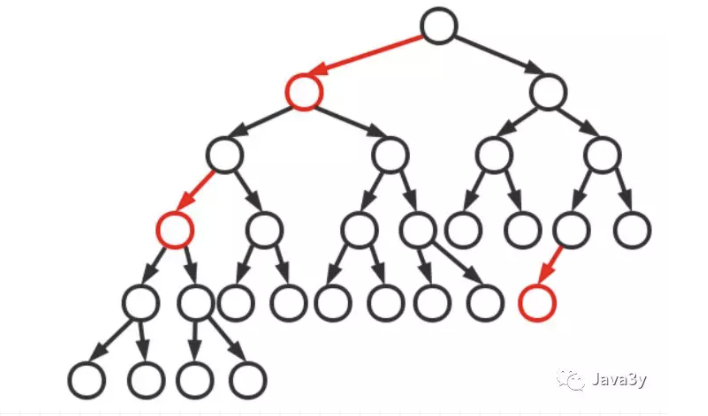
将红色节点的左链接画平之后：得到2-3平衡树:

image

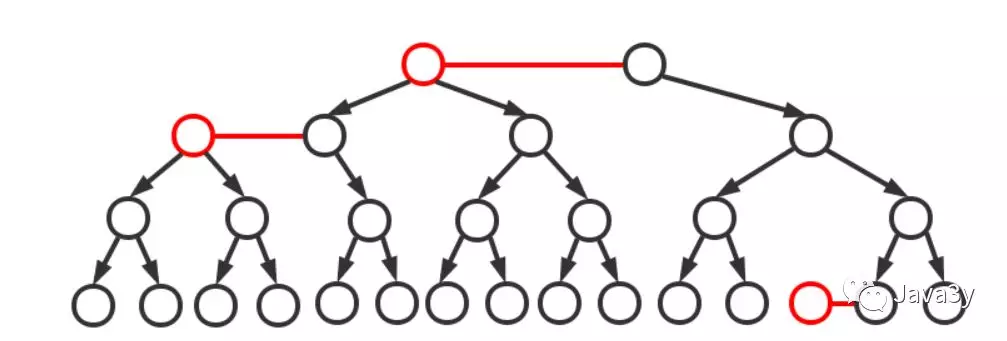
红黑树基础知识

前面已经说了，红黑树是在2-3的基础上实现的一种树，它能够用统一的方式完成所有变换。很好理解：红黑树也是平衡树的一种，在插入元素的时候它也得保持树的平衡，那红黑树是以什么的方式来保持树的平衡的呢？

 

红黑树用的是也是两种方式来替代2-3树不断的节点交换操作：

 

  • 旋转：顺时针旋转和逆时针旋转
  • 反色：交换红黑的颜色
  • 这个两个实现比2-3树交换的节点(合并，分解)要方便一些

 

红黑树为了保持平衡，还有制定一些约束，遵守这些约束的才能叫做红黑树：

 

    1. 红黑树是二叉搜索树。
    2. 根节点是黑色。
    3. 每个叶子节点都是黑色的空节点（NIL节点）。
    4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
    5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(每一条树链上的黑色节点数量（称之为“黑高”）必须相等)。
posted @ 2020-09-11 20:21  _bwang  阅读(411)  评论(0)    收藏  举报