洛谷 P4066 [SHOI2003]吃豆豆 解题报告

P4066 [SHOI2003]吃豆豆

题目描述

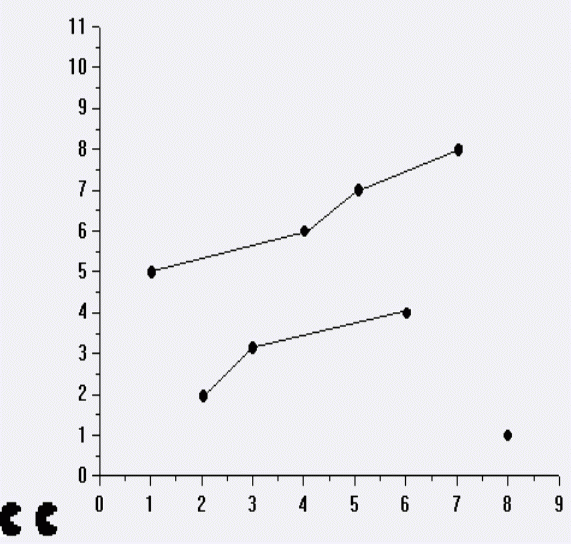
两个PACMAN吃豆豆。一开始的时候，PACMAN都在坐标原点的左下方，豆豆都在右上方。PACMAN走到豆豆处就会吃掉它。PACMAN行走的路线很奇怪，只能向右走或者向上走，他们行走的路线不可以相交。 请你帮这两个PACMAN计算一下，他们俩加起来最多能吃掉多少豆豆。

输入输出格式

输入格式：

第一行为一个整数N，表示豆豆的数目。 接下来 N 行，每行一对正整数，表示第i个豆豆的坐标。任意两个豆豆的坐标都不会重合。

输出格式：

仅有一行包含一个整数，即两个PACMAN加起来最多能吃掉的豆豆数量

输入输出样例

输入样例#1：

8
8 1
1 5
5 7
2 2
7 8
4 6
3 3
6 4

输出样例#1：

7

说明：

N < = 2000

---

先考虑暴力一点的

其实应该算是个比较裸的费用流建模了。

拆点分别连容量和权值边各为1，代表通过这个点获得1且仅可以走一次。

源点1连源点2容量2，表示两个人走。其余容量inf，权值为0

关于两个人相交的部分，其实是无所谓的，可以交换

直接跑最大费用最大流即可

---

考虑优化

连边时连接了很多无用的边，比如某两个点本来就间接可达，又连接了直接的边。

我们可以只连间接可达的边。然而这样会出现问题，因为我们限制了一个点只能走一次。

好办，我们把拆的点再连一个容量为inf，权值为0的点，代表可以多次走但不产生答案

关于连边，按两个关键字排序以后，从左往右只连接x递增而y递减的边。其实有点计算几何的影子

---

Code:

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
const int N=4050;
const int M=400010;
const int inf=0xcfcfcfcf;
int head[N],edge[M],f[M],to[M],Next[M],cnt=1,t,ans;
void add(int u,int v,int w,int flow)
{
    to[++cnt]=v;edge[cnt]=w;f[cnt]=flow;Next[cnt]=head[u];head[u]=cnt;
    to[++cnt]=u;edge[cnt]=-w;f[cnt]=0;Next[cnt]=head[v];head[v]=cnt;
}
std::pair <int,int > dx[N>>1];
int n;
std::queue <int > q;
int dis[N],used[N],pre[N];
bool spfa()
{
    memset(dis,0xcf,sizeof(dis));
    dis[0]=0;
    q.push(0);
    while(!q.empty())
    {
        int u=q.front();
        used[u]=0;
        q.pop();
        for(int i=head[u];i;i=Next[i])
        {
            int v=to[i],w=edge[i];
            if(f[i]&&dis[v]<dis[u]+w)
            {
                dis[v]=dis[u]+w;
                pre[v]=i;
                if(!used[v])
                {
                    used[v]=1;
                    q.push(v);
                }
            }
        }
    }
    return dis[t]!=inf;
}
void augment()
{
    ans+=dis[t];
    int now=t;
    while(now)
    {
        f[pre[now]^1]+=1;
        f[pre[now]]-=1;
        now=to[pre[now]^1];
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d%d",&dx[i].first,&dx[i].second);
    std::sort(dx+1,dx+1+n);
    for(int i=1;i<=n;i++)
    {
        int mi=-inf;
        for(int j=i+1;j<=n;j++)
            if(dx[j].second<mi&&dx[j].second>=dx[i].second)
            {
                add(i+n,j,0,-inf);
                mi=dx[j].second;
            }
    }
    t=n*2+2;
    for(int i=1;i<=n;i++)
    {
        add(i,i+n,1,1);
        add(i,i+n,0,-inf);
        add(n*2+1,i,0,-inf);
        add(i+n,t,0,-inf);
    }
    add(0,n*2+1,0,2);
    while(spfa())
        augment();
    printf("%d\n",ans);
    return 0;
}

---

2018.7.13