洛谷 P2233 [HNOI2002]公交车路线 解题报告
P2233 [HNOI2002]公交车路线
题目背景
在长沙城新建的环城公路上一共有8个公交站,分别为A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行,因此你从某一个公交站到另外一个公交站往往要换几次车,例如从公交站A到公交站D,你就至少需要换3次车。
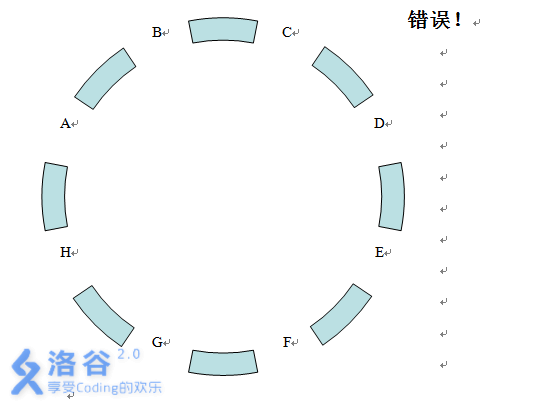
Tiger的方向感极其糟糕,我们知道从公交站A到公交E只需要换4次车就可以到达,可是tiger却总共换了n次车,注意tiger一旦到达公交站E,他不会愚蠢到再去换车。现在希望你计算一下tiger有多少种可能的乘车方案。
题目描述
输入输出格式
输入格式:
输入文件由bus.in读入,输入文件当中仅有一个正整数n(4<=n<=10000000),表示tiger从公交车站A到公交车站E共换了n次车。
输出格式:
输出到文件bus.out。输出文件仅有一个正整数,由于方案数很大,请输出方案数除以 1000后的余数。
先看普通的DP做法
\(dp[i][j]\)表示换了\(i\)次车目前在\(j\)车站的方案数
转移:\(dp[i][j]=dp[i-1][j-1]+dp[i-1][j+1]\)
发现每一轮都是一样的,每一个车站也是
考虑矩阵优化
初始矩阵为(1代表出发点)
0 0 0 0 1 0 0 0 0
单次操作矩阵为
0 0 0 0 0 0 0 0 0
1 0 1 0 0 0 0 0 0
0 1 0 1 0 0 0 0 0
0 0 1 0 1 0 0 0 0
0 0 0 1 0 1 0 0 0
0 0 0 0 1 0 1 0 0
0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0 1
0 0 0 0 0 0 0 0 0
矩阵快速幂即可
Code:
#include <cstdio>
#include <cstring>
#define mod 1000
struct matrix
{
int dx[10][10];
matrix()
{
memset(dx,0,sizeof(dx));
}
matrix friend operator *(matrix n1,matrix n2)
{
matrix n3;
for(int i=1;i<=9;i++)
for(int j=1;j<=9;j++)
for(int k=1;k<=9;k++)
n3.dx[i][j]=(n3.dx[i][j]+n1.dx[i][k]*n2.dx[k][j])%mod;
return n3;
}
};
matrix quick_pow(matrix d,int k)
{
matrix f;
for(int i=1;i<=9;i++) f.dx[i][i]=1;
while(k)
{
if(k&1)
f=f*d;
d=d*d;
k>>=1;
}
return f;
}
int main()
{
int n;
scanf("%d",&n);
matrix d;
for(int i=2;i<=8;i++)
d.dx[i][i+1]=1;
for(int i=2;i<=8;i++)
d.dx[i][i-1]=1;
d=quick_pow(d,n);
printf("%d\n",(d.dx[5][1]+d.dx[5][9])%mod);
return 0;
}
2018.7.13


 浙公网安备 33010602011771号
浙公网安备 33010602011771号