「NOI2016」网格 解题报告
「NOI2016」网格
容易注意到,答案最多为2,也就是说答案为-\(1,0,1,2\)四种,考虑逐个判断。
无解的情况比较简单
如果\(nm\le c+1\),显然无解
如果\(nm=c+2\),判断2个跳蚤(如无说明,以下白点指跳蚤)是否四联通(如无说明,以下联通均指四联通),如果是,无解。
先不考虑复杂度
\(0\)的情况,就是白点有两个以上联通块,可以直接bfs判断
\(1\)的情况,就是白点存在割点,可以通过tarjan判断
\(2\)的情况,就是其他情况
这样的复杂度是\(O(Tnm)\)的
考虑可能成为割点的点其实不多,定义它们为关键点,然后提取关键点再进行操作
我们发现,只有黑点(以下均指蛐蛐)周围8联通的8个格子可能成为割点
我们把这些点拎出来,编一个号然后对每个白点联通块跑tarjan判断割点,就可以判断原图是否有割点。
但是只提出可能成为割点的点建出的图可能会把不是割点的点判断成割点
比如这种情况
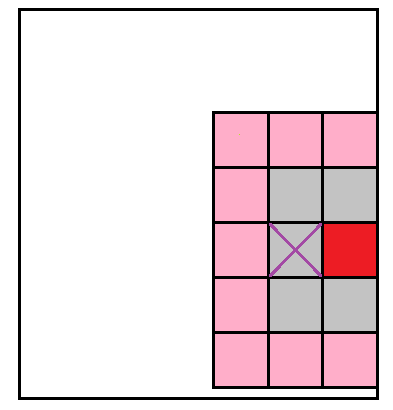
黑点是红色的,建出\(3\times 3\)会使打叉的点成为割点,但实际上它不是
所以我们需要提取以黑点为中心的\(5\times 5\)个格子
这样就可以判断答案是否为\(1\)了
然后如何判断白点的连通性呢?
还是只考虑关键点,我们用并查集处理出每个关键点白点所在的联通块编号,然后遍历每个黑点联通块,如果某个黑点联通块边界接触到了至少两个不同的白点联通块,那么这个白点就是不连通的了。
考虑特殊情况,我们上面提取关键点后\(n=1\)或者\(m=1\)的情况就无法判断了,进行特判。
考虑实现,因为点数实际上比较大,如果用\(map\)去定位关键点会很慢,考虑使用Hash定位关键点
总复杂度\(O(\sum c)\)
Code:
#include <cstdio>
#include <cctype>
#include <cmath>
#include <algorithm>
using std::min;
using std::max;
const int SIZE=1<<21;
char ibuf[SIZE],*iS,*iT;
//#define gc() (iS==iT?(iT=(iS=ibuf)+fread(ibuf,1,SIZE,stdin),iS==iT?EOF:*iS++):*iS++)
#define gc() getchar()
template <class T>
void read(T &x)
{
x=0;char c=gc();
while(!isdigit(c)) c=gc();
while(isdigit(c)) x=x*10+c-'0',c=gc();
}
const int N=2e6+5e5+10;
const int mod=19260817;
int n,m,c,dx[N],dy[N];
void ckmin(int &x,int y){x=x<y?x:y;}
void ckmax(int &x,int y){x=x>y?x:y;}
struct Hash
{
int dx[N],dy[N],dis[N],is[N];
int head[mod],Next[N],cnt;
void ins(int x,int y,int isbla,int d)//ququ is 1
{
if(x<=0||y<=0||x>=n+1||y>=m+1) return;
int p=(1ll*(x-1)*m+y)%mod;
for(int i=head[p];i;i=Next[i])
if(dx[i]==x&&dy[i]==y)
{
ckmin(dis[i],d);
ckmax(is[i],isbla);
return;
}
Next[++cnt]=head[p],head[p]=cnt;
dx[cnt]=x,dy[cnt]=y,dis[cnt]=d,is[cnt]=isbla;
}
int qry(int x,int y)
{
if(x<=0||y<=0||x>=n+1||y>=m+1) return -1;
int p=(1ll*(x-1)*m+y)%mod;
for(int i=head[p];i;i=Next[i])
if(dx[i]==x&&dy[i]==y)
return i;
return -1;
}
void clear()
{
for(int i=1;i<=cnt;i++)
{
head[(1ll*(dx[i]-1)*m+dy[i])%mod]=0;
dx[i]=dy[i]=dis[i]=is[i]=Next[i]=0;
}
cnt=0;
}
}Ha;
//int ct=0;
bool ck()
{
if(1ll*n*m<=c+1) return true;
if(1ll*n*m==c+2)
{
//++ct;
/*printf("ct is:%d\n",ct);
if(ct==5)
{
puts("");
}*/
int kx[5]={},ky[5]={};
for(int i=1;i<=c;i++)
Ha.ins(dx[i],dy[i],1,0);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(Ha.qry(i,j)==-1)
{
kx[++kx[0]]=i;
ky[++ky[0]]=j;
}
int d=abs(kx[1]-kx[2])+abs(ky[1]-ky[2]);
Ha.clear();
if(d==1) return true;
}
return false;
}
const int px[5]={0,-1,0,1,0};
const int py[5]={0,0,-1,0,1};
int f[N],vis[N];
int Find(int x){return f[x]=f[x]==x?x:Find(f[x]);}
void Merge(int x,int y)
{
f[Find(y)]=Find(x);
}
void dfs(int x,int y,int anc)
{
int now=Ha.qry(x,y);
if(now==-1||Ha.is[now]||vis[now]) return;
vis[now]=1;
Merge(anc,now);
for(int i=1;i<=4;i++)
{
int tx=x+px[i],ty=y+py[i];
dfs(tx,ty,anc);
}
}
void dfs(int x,int y,int col,int &flag)
{
int now=Ha.qry(x,y);
if(now==-1||vis[now]||flag) return;
vis[now]=1;
for(int i=1;i<=4;i++)
{
int tx=x+px[i],ty=y+py[i],to=Ha.qry(tx,ty);
if(to!=-1&&!Ha.is[to])
{
if(!col) col=Find(to);
else if(col!=Find(to))
{
flag=1;
return;
}
}
}
for(int i=1;i<=4;i++)
{
int tx=x+px[i],ty=y+py[i];
dfs(tx,ty,col,flag);
}
}
bool ck0()
{
for(int i=1;i<=Ha.cnt;i++) f[i]=i,vis[i]=0;
for(int i=1;i<=Ha.cnt;i++)
if(!Ha.is[i]&&!vis[i])
dfs(Ha.dx[i],Ha.dy[i],i);
int flag=0;
for(int i=1;i<=Ha.cnt;i++)
if(Ha.is[i]&&!vis[i])
{
dfs(Ha.dx[i],Ha.dy[i],0,flag);
if(flag) return true;
}
return false;
}
int head[N],to[N<<2],Next[N<<2],cnt;
void add(int u,int v)
{
to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;
}
int dfn[N],low[N],dfsclock;
void tarjan(int now,int fa,int &cut)
{
if(cut) return;
dfn[now]=low[now]=++dfsclock;
int chi=0;
for(int v,i=head[now];i&&!cut;i=Next[i])
if((v=to[i])!=fa)
{
if(!dfn[v])
{
++chi;
tarjan(v,now,cut);
if(low[v]>=dfn[now]&&now!=fa&&Ha.dis[now]==1)
{
cut=1;
return;
}
low[now]=min(low[now],low[v]);
}
else
low[now]=min(low[now],dfn[v]);
}
if(now==fa&&chi>1&&Ha.dis[now]==1) cut=1;
}
void work()
{
read(n),read(m),read(c);
for(int i=1;i<=c;i++) read(dx[i]),read(dy[i]);
if(ck())
{
puts("-1");
return;
}
if(n==1)
{
std::sort(dy+1,dy+1+c);
int ans=1,p=1;
while(p<=c)
{
int loc=p;
while(loc<=c&&dy[loc+1]==dy[loc]+1) ++loc;
if(dy[p]>1&&dy[p]<m)
{
ans=0;
break;
}
p=loc+1;
}
printf("%d\n",ans);
return;
}
if(m==1)
{
std::sort(dx+1,dx+1+c);
int ans=1,p=1;
while(p<=c)
{
int loc=p;
while(loc<=c&&dx[loc+1]==dx[loc]+1) ++loc;
if(dx[p]>1&&dx[p]<n)
{
ans=0;
break;
}
p=loc+1;
}
printf("%d\n",ans);
return;
}
for(int x,y,i=1;i<=c;i++)
{
x=dx[i],y=dy[i];
for(int j=-2;j<=2;j++)
for(int k=-2;k<=2;k++)
{
int d=max(abs(j),abs(k));
if(!j&&!k) Ha.ins(x+j,y+k,1,d);
else Ha.ins(x+j,y+k,0,d);
}
}
for(int x,y,i=1;i<=Ha.cnt;i++)
{
if(Ha.is[i]) continue;
x=Ha.dx[i],y=Ha.dy[i];
for(int l=1;l<=4;l++)
{
int tx=x+px[l],ty=y+py[l];
int v=Ha.qry(tx,ty);
if(~v&&!Ha.is[v]) add(i,v);
}
}
if(ck0())
{
puts("0");
for(int i=1;i<=Ha.cnt;i++) head[i]=0;
cnt=0;
Ha.clear();
return;
}
int cut=0;
for(int i=1;i<=Ha.cnt;i++)
if(!dfn[i])
{
tarjan(i,i,cut);
if(cut) break;
}
if(cut) puts("1");
else puts("2");
for(int i=1;i<=Ha.cnt;i++)
head[i]=dfn[i]=low[i]=0;
cnt=dfsclock=0;
Ha.clear();
}
int main()
{
int T;read(T);
while(T--) work();
return 0;
}
2019.5.31


 浙公网安备 33010602011771号
浙公网安备 33010602011771号