数据结构之平衡二叉树

1.背景

面试中经常问到关于二叉平衡树的知识点

2.左旋

 

 

 /**
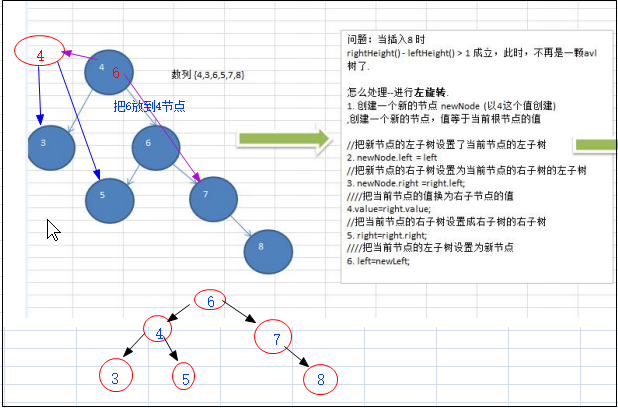
     * 左旋
     * 右边高就左旋
     */
    public void leftRotate() {
        // 定义一个新的当前节点
        Node nodeNew = new Node(value);
        // 新节点的左节点为:当前节点的左节点
        nodeNew.leftNode = leftNode;
        // 新节点的右节点:当前节点的右节点的左节点
        nodeNew.rightNode = rightNode.leftNode;
        // 值替换:当前节点的值替换为当前节点右节点的值
        value = rightNode.value;
        // 当前节点的左节点为: 新的节点
        leftNode = nodeNew;
        // 当前节点的右节点为: 当前节点的右节点的右节点
        rightNode = rightNode.rightNode;
    }

 

3.右旋

 

 

 /**
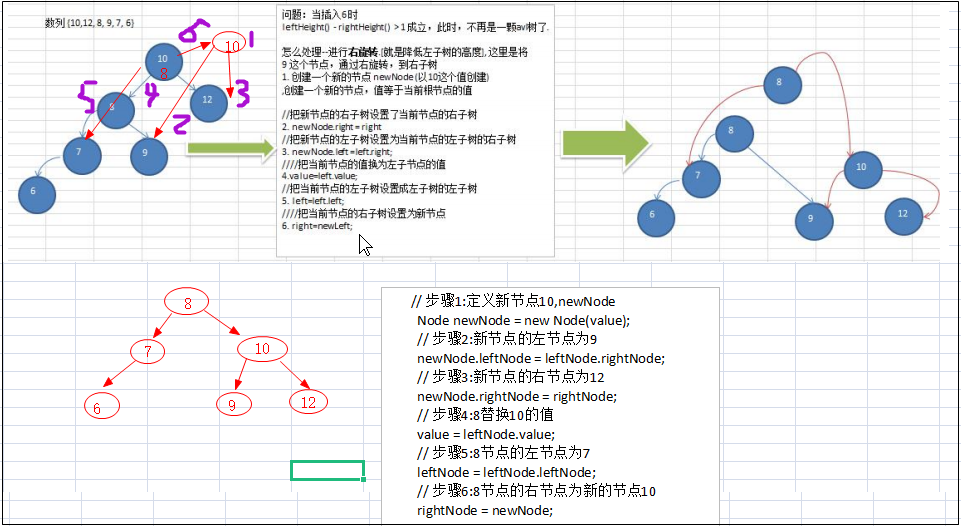
     * 右旋
     * 左边边高就右旋
     */
    public void rightRotate() {
        // 步骤1:定义新节点10,newNode
        Node newNode = new Node(value);
        // 步骤2:新节点的左节点为9
        newNode.leftNode = leftNode.rightNode;
        // 步骤3:新节点的右节点为12
        newNode.rightNode = rightNode;
        // 步骤4:8替换10的值
        value = leftNode.value;
        // 步骤5:8节点的左节点为7
        leftNode = leftNode.leftNode;
        // 步骤6:8节点的右节点为新的节点10
        rightNode = newNode;
    }

 

4.双旋

 

 

 /**
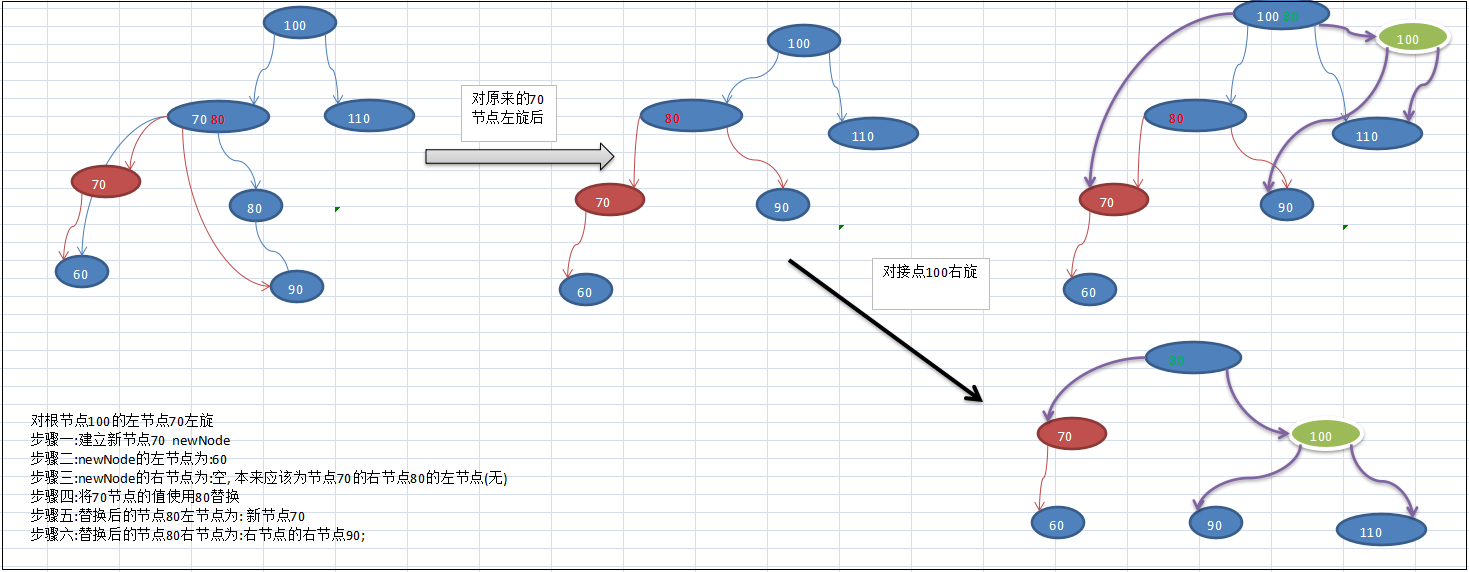
     * 添加一个节点
     *
     * @param node
     */
    public void add(Node node) {
        if (node.value < this.value) { // 放在左边
            if (this.leftNode == null) {
                this.leftNode = node;
            } else {
                this.leftNode.add(node);
            }
        } else {// 放在右边
            if (this.rightNode == null) {
                this.rightNode = node;
            } else {
                this.rightNode.add(node);
            }
        }
        // 当添加完节点后,如果(右子树的高度-左子树的高度>1),左旋
        if (rightHeight() - leftHeight() > 1) {
            // 如果(它的右子树的左子树高度-它的右子树的右子树高度>0)
            if (rightNode != null && rightNode.leftHeight() - rightNode.rightHeight() > 0) {
                // 先对右子节点进行右旋
                rightNode.rightRotate();
                // 然后在对当前节点进行左旋
                leftRotate();
            } else {
                // 直接左旋
                leftRotate();
            }
            // 当前情况处理完成后返回,避免继续往下面执行
            return;
        }
        // 当添加完成一个节点后,如果(左子树的高度-右子树的高度>1),右旋
        if (leftHeight() - rightHeight() > 1) {
            // 如果它的左子树的右子树高度大于它的左子树的左子树的高度
            if (leftNode != null && leftNode.rightHeight() - leftNode.leftHeight() > 0) {
                // 它的左子树左旋
                leftNode.leftRotate();
                // 当前节点右旋
                rightRotate();
            } else {
                // 当前节点右旋
                rightRotate();
            }
            return;
        }
    }

 

 

5.代码

package com.ldp.structure.demo08AVLTree;

import org.junit.Test;

/**
 * @create 05/03 11:18
 * @description <p>
 * 二叉平衡树
 * </p>
 */
public class Test01 {
    /**
     * 二叉排序树,添加测试
     */
    @Test
    public void test01() {
        int[] array = {100, 110, 70, 80, 60, 90};
        BstTree bstTree = new BstTree();
        // 添加到二叉树
        for (int i : array) {
            bstTree.add(new Node(i));
        }
        // 中序遍历
        bstTree.middleList();
    }
}

class BstTree {
    Node root;

    /**
     * 添加节点
     *
     * @param node
     */
    public void add(Node node) {
        if (root == null) {
            root = node;
        } else {
            root.add(node);
        }
    }

    /**
     * 删除节点
     *
     * @param value
     */
    public void delete(Integer value) {
        Node targetNode = getTargetNode(value);
        if (targetNode == null) {
            System.out.println("该节点不存在:value=" + value);
            return;
        }
        Node targetNodeParent = getTargetNodeParent(value);
        // 1.待删除的节点有零个叶子节点(本身是叶子节点)
        if (targetNode.leftNode == null && targetNode.rightNode == null) {
            deleteZero(targetNodeParent, value);
            System.out.println("节点删除成功:value=" + value);
        } else if (targetNode.leftNode != null && targetNode.rightNode != null) {
            // 3.待删除的节点有两个叶子节点
            deleteTwo(targetNode);
            System.out.println("节点删除成功:value=" + value);
        } else {
            // 2.待删除的节点有一个叶子节点
            deleteOne(targetNodeParent, targetNode, value);
            System.out.println("节点删除成功:value=" + value);
        }
    }

    /**
     * 待删除的节点有零个叶子节点(本身是叶子节点)
     * 1.找到待删除的节点 targetNode;
     * 2.找到targetNode的父节点 parentNode;
     * 3.判定targetNode是parentNode的左节点还是右节点
     * 如果targetNode是parentNode的左节点:parentNode.leftNode=null;
     * 如果targetNode是parentNode的右节点:parentNode.rightNode=null;
     */
    private void deleteZero(Node nodeParent, Integer value) {
        if (nodeParent == null) {
            root = null;
            return;
        }
        if (nodeParent.leftNode.value == value) {
            nodeParent.leftNode = null;
        } else {
            nodeParent.rightNode = null;
        }
    }

    /**
     * 待删除的节点有一个叶子节点
     * 1.找到待删除的节点 targetNode;
     * 2.找到targetNode的父节点 parentNode;
     * 3.判定targetNode是parentNode的左节点还是右节点
     * 如果targetNode是parentNode的左节点:
     * 且targetNode的叶子节点是左节点:parentNode.leftNode=targetNode.leftNode
     * 且targetNode的叶子节点是右节点:parentNode.leftNode=targetNode.rightNode
     * 如果targetNode是parentNode的右节点:
     * 且targetNode的叶子节点是左节点:parentNode.rightNode=targetNode.leftNode
     * 且targetNode的叶子节点是右节点:parentNode.rightNode=targetNode.rightNode
     */
    private void deleteOne(Node nodeParent, Node targetNode, Integer value) {
        Node tempNode;
        if (targetNode.leftNode != null) {// targetNode的叶子节点是左节点
            tempNode = targetNode.leftNode;
        } else {
            tempNode = targetNode.rightNode;
        }
        // 如果父节点为空
        if (nodeParent == null) {
            root = tempNode;
            return;
        }
        if (nodeParent.leftNode != null && nodeParent.leftNode.value == value) {// 如果targetNode是parentNode的左节点
            nodeParent.leftNode = tempNode;
        } else {
            nodeParent.rightNode = tempNode;
        }
    }

    /**
     * 待删除的节点有两个叶子节点
     * 1.找到待删除的节点 targetNode;
     * 2.targetNode的右节点开始找,找到最小节点
     * 3.用一个临时节点minNode保存
     * 4.删除最小节点
     * 5.targetNode.value=minNode.value
     *
     * @param targetNode
     */
    private void deleteTwo(Node targetNode) {
        Node minNodeParent = targetNode;
        Node minNode = targetNode.rightNode;
        if (targetNode.rightNode.leftNode == null) { // 如果股目标节点的右节点没有左子节点,则右节点是最小节点
            minNodeParent.rightNode = null;
            targetNode.value = minNode.value;
        } else {// 如果股目标节点的右节点有左子节点,则一直往最左边找,最后一个左节点是最小节点
            while (true) {
                if (minNode.leftNode != null) {
                    minNodeParent = minNode;
                    minNode = minNode.leftNode;
                } else {
                    break;
                }
            }
            minNodeParent.leftNode = null;
            targetNode.value = minNode.value;
        }
    }


    /**
     * 根据value找到目标节点
     *
     * @param value
     * @return
     */
    public Node getTargetNode(Integer value) {
        Node tempNode = root;
        while (tempNode != null) {
            if (tempNode.value.equals(value)) {// 已找到
                break;
            } else if (value < tempNode.value) {
                tempNode = tempNode.leftNode;
            } else {
                tempNode = tempNode.rightNode;
            }
        }
        return tempNode;
    }

    /**
     * 根据value找到目标节点的父节点
     *
     * @param value
     * @return
     */
    public Node getTargetNodeParent(Integer value) {
        if (this.root.value.equals(value)) {
            System.out.println("该节点没有父节点.....");
            return null;
        }
        Node parentNode = null;
        Node tempNode = root;
        while (tempNode != null) {
            if (tempNode.value.equals(value)) {// 已找到
                break;
            } else if (value < tempNode.value) {
                parentNode = tempNode;
                tempNode = tempNode.leftNode;
            } else {
                parentNode = tempNode;
                tempNode = tempNode.rightNode;
            }
        }
        if (tempNode == null) {
            return null;
        }
        return parentNode;
    }

    public void middleList() {
        if (root == null) {
            System.out.println("节点为空...");
        } else {
            root.middleList();
        }
    }
}

class Node {
    Integer value;
    Node leftNode;
    Node rightNode;

    public Node(Integer value) {
        this.value = value;
    }

    /**
     * 添加一个节点
     *
     * @param node
     */
    public void add(Node node) {
        if (node.value < this.value) { // 放在左边
            if (this.leftNode == null) {
                this.leftNode = node;
            } else {
                this.leftNode.add(node);
            }
        } else {// 放在右边
            if (this.rightNode == null) {
                this.rightNode = node;
            } else {
                this.rightNode.add(node);
            }
        }
        // 当添加完节点后,如果(右子树的高度-左子树的高度>1),左旋
        if (rightHeight() - leftHeight() > 1) {
            // 如果(它的右子树的左子树高度-它的右子树的右子树高度>0)
            if (rightNode != null && rightNode.leftHeight() - rightNode.rightHeight() > 0) {
                // 先对右子节点进行右旋
                rightNode.rightRotate();
                // 然后在对当前节点进行左旋
                leftRotate();
            } else {
                // 直接左旋
                leftRotate();
            }
            // 当前情况处理完成后返回,避免继续往下面执行
            return;
        }
        // 当添加完成一个节点后,如果(左子树的高度-右子树的高度>1),右旋
        if (leftHeight() - rightHeight() > 1) {
            // 如果它的左子树的右子树高度大于它的左子树的左子树的高度
            if (leftNode != null && leftNode.rightHeight() - leftNode.leftHeight() > 0) {
                // 它的左子树左旋
                leftNode.leftRotate();
                // 当前节点右旋
                rightRotate();
            } else {
                // 当前节点右旋
                rightRotate();
            }
            return;
        }
    }

    /**
     * 中序遍历
     */
    public void middleList() {
        if (this.leftNode != null) {
            this.leftNode.middleList();
        }
        System.out.println(this);
        if (this.rightNode != null) {
            this.rightNode.middleList();
        }
    }

    public int leftHeight() {
        if (leftNode == null) {
            return 0;
        }
        return leftNode.height();
    }

    public int rightHeight() {
        if (rightNode == null) {
            return 0;
        }
        return rightNode.height();
    }

    /**
     * 计算树的高度
     *
     * @return
     */
    public Integer height() {
        return Math.max(leftNode == null ? 0 : leftNode.leftHeight(), rightNode == null ? 0 : rightNode.rightHeight()) + 1;
    }

    /**
     * 左旋
     * 右边高就左旋
     */
    public void leftRotate() {
        // 定义一个新的当前节点
        Node nodeNew = new Node(value);
        // 新节点的左节点为:当前节点的左节点
        nodeNew.leftNode = leftNode;
        // 新节点的右节点:当前节点的右节点的左节点
        nodeNew.rightNode = rightNode.leftNode;
        // 值替换:当前节点的值替换为当前节点右节点的值
        value = rightNode.value;
        // 当前节点的左节点为: 新的节点
        leftNode = nodeNew;
        // 当前节点的右节点为: 当前节点的右节点的右节点
        rightNode = rightNode.rightNode;
    }

    /**
     * 右旋
     * 左边边高就右旋
     */
    public void rightRotate() {
        // 步骤1:定义新节点10,newNode
        Node newNode = new Node(value);
        // 步骤2:新节点的左节点为9
        newNode.leftNode = leftNode.rightNode;
        // 步骤3:新节点的右节点为12
        newNode.rightNode = rightNode;
        // 步骤4:8替换10的值
        value = leftNode.value;
        // 步骤5:8节点的左节点为7
        leftNode = leftNode.leftNode;
        // 步骤6:8节点的右节点为新的节点10
        rightNode = newNode;
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }
}

 

完美!