位置化数字系统
位置化数字系统,符号S占据的位置决定了数字表示的值。
数字表示为:$\pm(S_{k-1}...S_2S_1S_0.S_{-1}S_{-2}...S_{-l})_b$
数字的值为:$\pm$ $S_{k-1} \times b^{k-1} +...+ S_1 \times b^1 +S_0 \times b^0$ + $S_{-1} \times b^{-1} +S_{-2} \times b^{-2} +...+S_{-l} \times b^{-l}$,b是底。
一、 常用进制
十进制: 以10为底(基数),即b=10;且用十个符号表示一个数,符号集为S{0,1, 2, 3, 4, 5, 6, 7, 8, 9}。
二进制: 以2为底(基数),即b=2;且用两个符号表示一个数,符号集为S{0, 1}。
八进制: 以8为底(基数),即b=8;且用八个字符表示一个数,符号集为S{0, 1, 2, 3, 4, 5, 6, 7}。
十六进制: 以16为底(基数),即b=16;且用十六个字符表示一个数,符号集为S{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}。英文字母A、B、C、D、E、F分别代表10、11、12、13、14、15。
二、进制转换
-
不常用八进制和十六进制表示实数。
1. R进制转十进制
十进制转十进制:
eg:$(24.13)_{10}$ = $ 2\times10^{1} + 4\times10^{0} $ + $1\times10^{-1} +3\times10^{-2}$ = $(24.13)_{10}$
二进制转十进制:
eg:$(101.11)_2$ = $ 1\times2^2 + 0\times2^1 + 1 \times2^0$ + $1\times2^{-1} + 1\times2^{-2}$ = $(5.751)_{10}$
八进制转十进制:
eg:$(1256)_8$ = $ 1\times8^3 + 2\times8^2 + 5\times8^2 + 6 \times 8^0 $ = $(686)_{10}$
十六进制转十进制:
eg:$(2AE)_{16}$ = $ 2\times16^2 + 10\times16^1 + 14\times16^0 $ = $(686)_{10}$
2. 十进制转R进制
-
整数部分: 除底取余,逆序排列。
eg:将十进制的35转换成二进制数。
$35=(100011)_2$
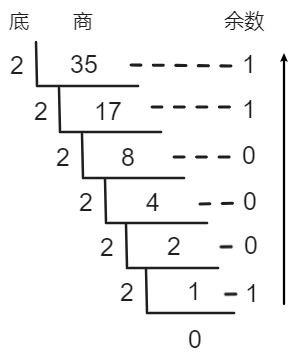
十进制数除以底,得到的商继续除底,直至商为0,然后反向取余数。直至商为0,然后反向取余数。
-
实数部分: 乘底取整,顺序排列。
eg:将十进制的85转化成八进制数。(精确小数点后4位)
$0.634=(0.5044)_8$

小数乘底,取整数,再将小数乘底,取整数,直至小数为零或目标位数足够。
-
十进制转二进制的变通方法
$2^7 \quad 2^6 \quad 2^5 \quad 2^4 \quad 2^3 \quad 2^2 \quad 2^1 \quad 2^0 = 128 \quad 64 \quad 32 \quad 16 \quad 8 \quad 4 \quad 2 \quad 1$
$2^{-1} \quad 2^{-2} \quad 2^{-3} \quad 2^{-4} \quad 2^{-5} \quad 2^{-6} \quad 2^{-7} = \frac{1}{2} \quad \frac{1}{4} \quad \frac{1}{16} \quad \frac{1}{32} \quad \frac{1}{64} \quad \frac{1}{128}$
3. 二进制与八进制
- 3位=1位
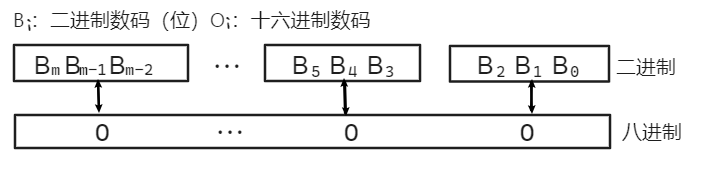
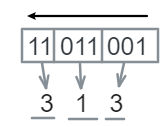
- 二进制转八进制: 从右至左
eg:$(11 \, 001 \, 011)_2 =(313)_8$
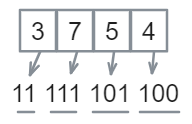
- 八进制转二进制
eg:$(3754)_8 =(11 \, 111 \, 101 \, 100)_2$
4. 二进制与十六进制
- 4位=1位
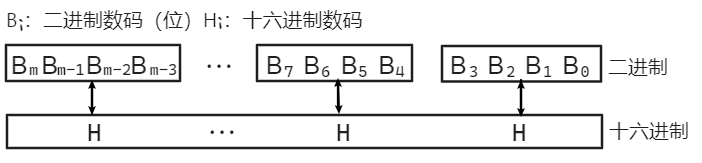
- 二进制转十六进制: 从右至左
eg:$(10 \, 1100 \, 1011)_2 = (2CB)_{16}$
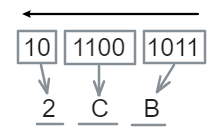
- 十六进制转二进制:
eg:$(4B39F)_{16} = (100 \, 1011 \, 0011 \, 1001 \, 1111)_2$
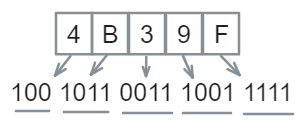
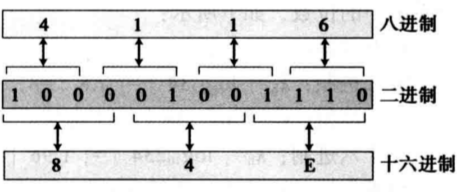
5.八进制与十六进制
- 八进制与十六进制通过二进制相互转化。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号