Leetcode 262周赛 题解

Leetcode 232周赛

备注：由于学校基本上安全方向学习为零，个人也有在刷leetcode为了后续面开发岗做准备 232周赛是碰巧看到的 个人感觉题目难度适中(并不是说没打过acm的小菜鸟没办法接受的) 挺适合开拓思路的

仅执行一次字符串交换能否使两个字符串相等

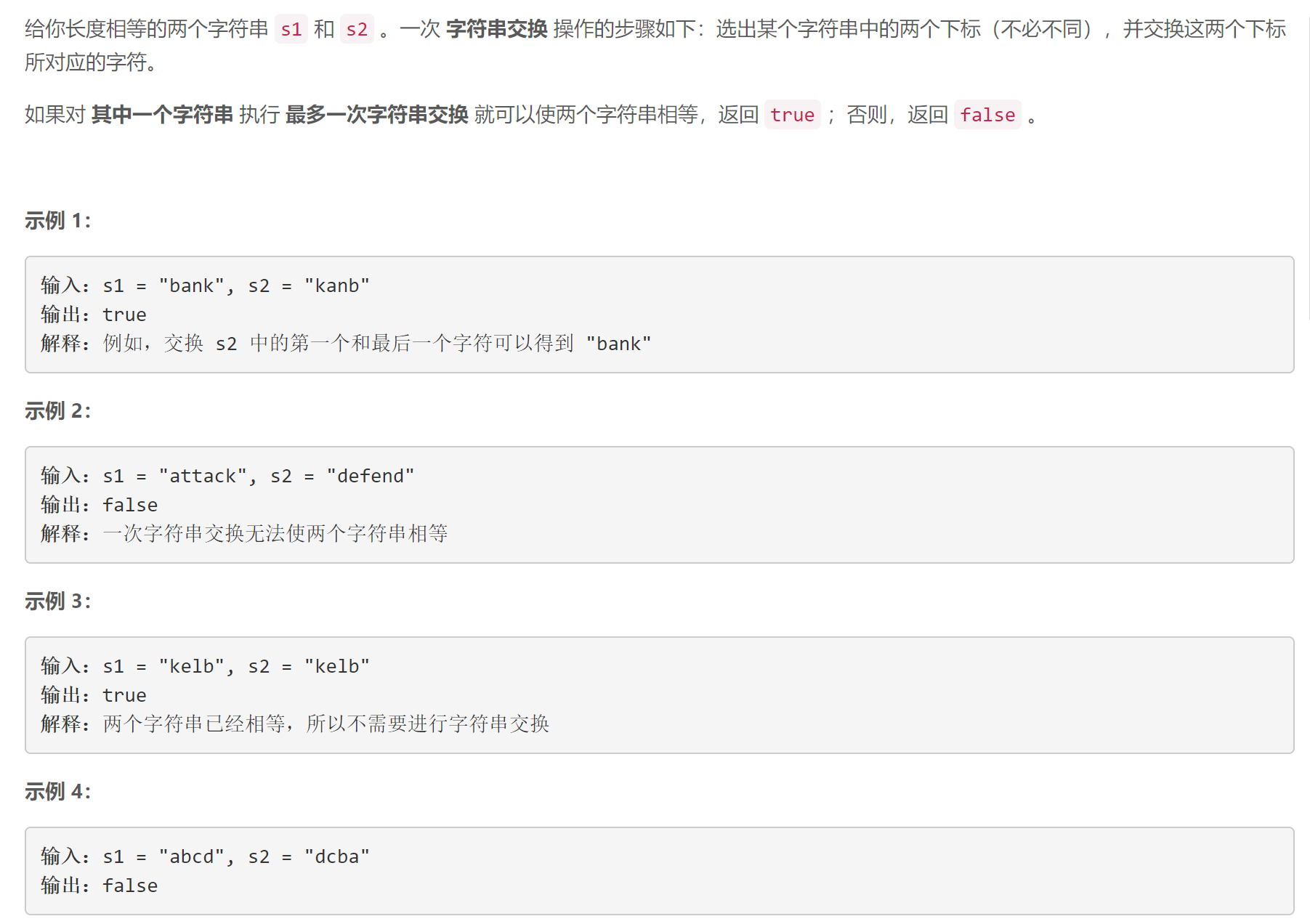
相对来说比较简单，基本上就是需要注意字符串相等的情况即可，基本上定义一个数组保存一下第n个不同的位置，然后判断如果不为2或0就是不符合要求，如果是2，则需要交换相同才可，否则不满足要求

class Solution {
public:
    bool areAlmostEqual(string s1, string s2) {
        //存储字符串不相同的位置
        vector<int> flag(s1.length(),0);
        int count = 0,len = s1.length();
        for(int i = 0;i<len;i++)
            if(s1[i]!=s2[i])
                flag[count++] = i;
        if(count == 0)  return true;
        if(count == 1 || count >= 3)    return false;
        if(count == 2)
            if(s1[flag[0]] == s2[flag[1]] && s1[flag[1]] == s2[flag[0]])
                return true;
        return false;
    }
};

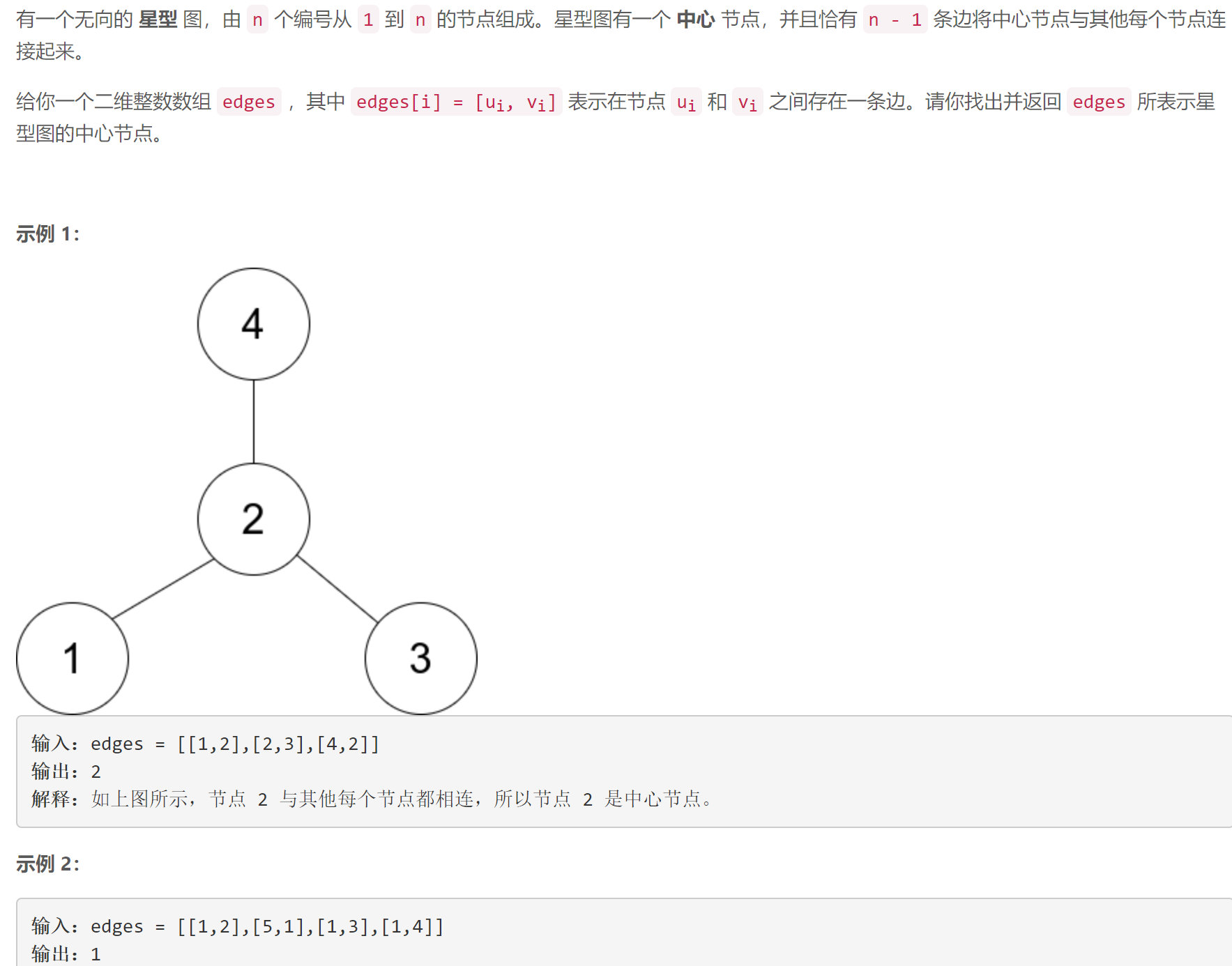
找出星型图的中心节点

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int p1=edges[0][0],p2=edges[0][1],p3=edges[1][0],p4=edges[1][1];
        if(p1==p3 || p1==p4)    return p1;
        if(p2==p3 || p2==p4)    return p2;
        return p1;
    }
};

emmm，题目相对来说可能有点打反向思维，因为无论如何任意两个边都是有一个公共点，就是正中心的那个点，因此只需要取前两个边的四个点，返回两个相同值的点即可

最大平均通过率

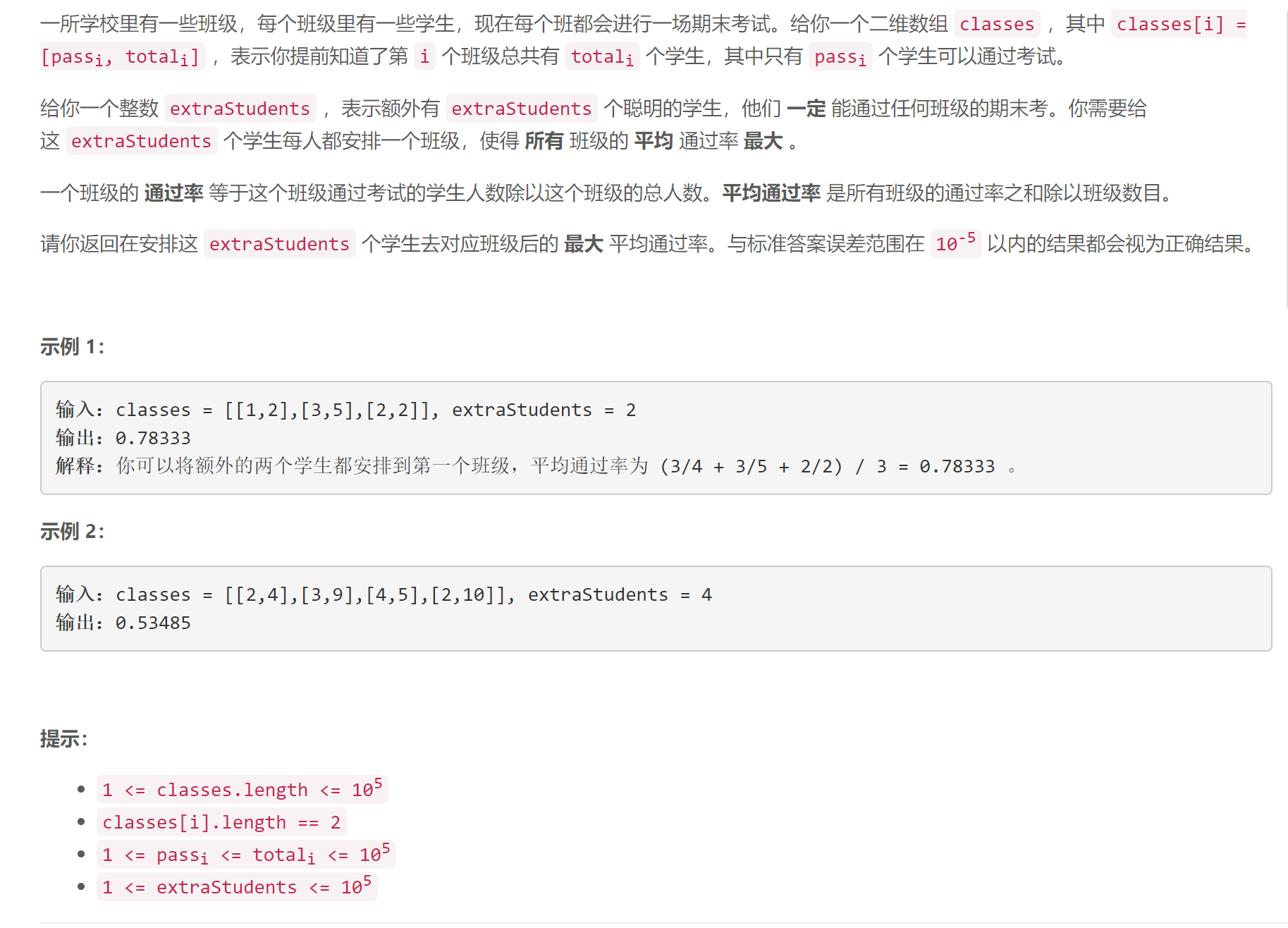
整体思路大概就是因为我们如果想要平均率的最大化，应该是优先以提高人数较少的班级为目标(理论上，可以用极限来证明)，但是基本上可以认为是常识，人数越多，相对来说人的班级来一个优等生，班级平均分也不会提高很多，但是反而只有俩人的班级，来一个优等生，班级平均分会显著提高，然后以一个数组保存当前所有班级的人数，将当前最少的班级的人数加上去

class Solution {
public:
    //increase返回当前人数增加一人后班级通过率增长的幅度
    double increase(int x,int y){
        return double(x+1) / double(y+1) - double(x) / double(y); 
    }
    double maxAverageRatio(vector<vector<int>>& classes, int extraStudents) {
        //优先队列自动排序increase最大的班级
        priority_queue<tuple<double,int,int>> q;
        int len = classes.size();
        double res = 0.0;
        for(int i = 0;i<len;i++){
            res += double(classes[i][0]) / double(classes[i][1]);
            q.emplace(increase(classes[i][0],classes[i][1]),classes[i][0],classes[i][1]);
        }
        for(int i = 0;i<extraStudents;i++){
            double d;int x,y;
            //tie解包tuple
            tie(d,x,y) = q.top();
            q.pop();
            res += increase(x,y);
            q.emplace(increase(x+1,y+1),x+1,y+1);
        }
        return res / len;
    }
};

好子数组的最大分数

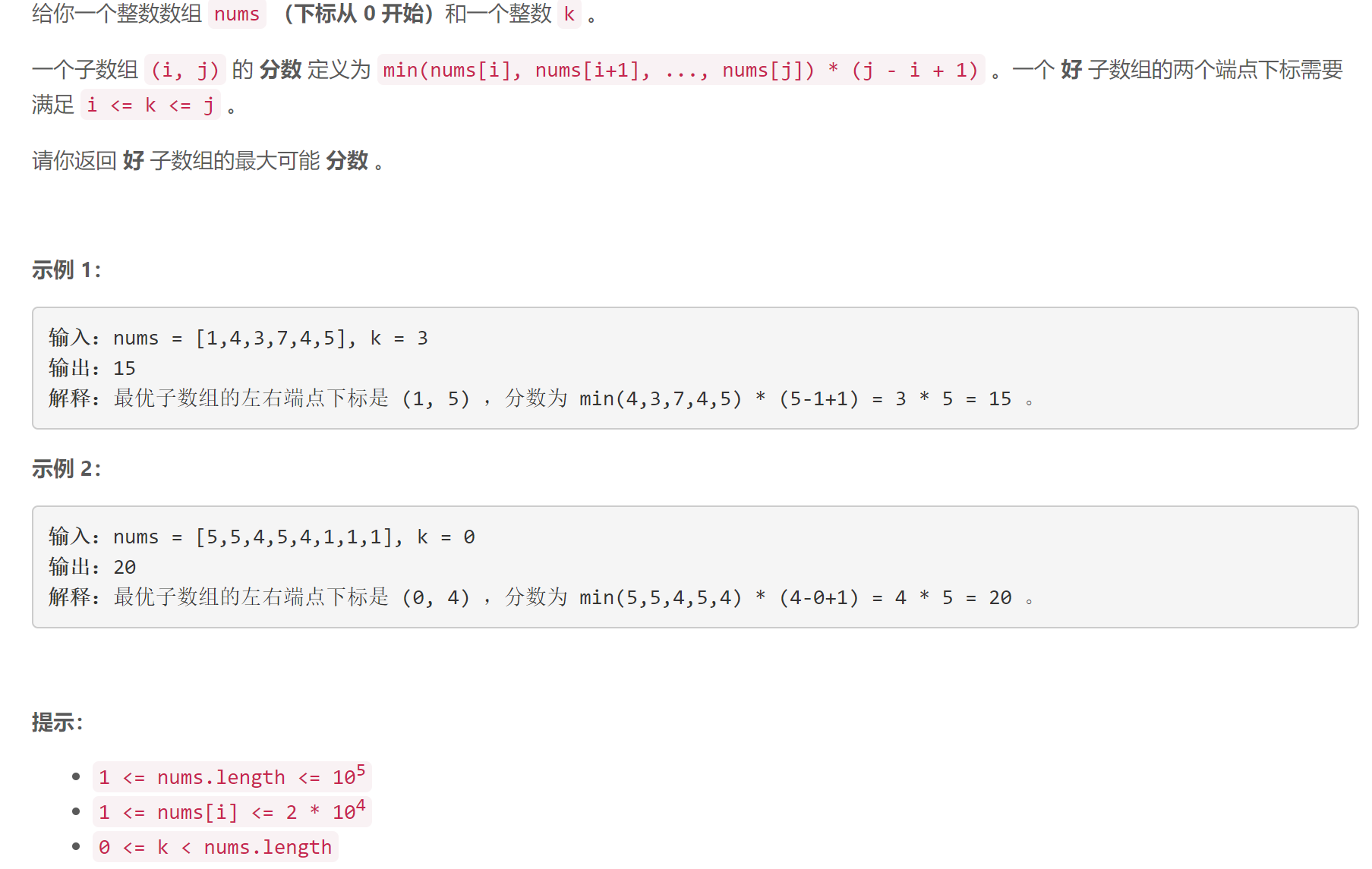
hard题，开始想了半天没想出来，后来看了一眼题解瞬间顿悟（还是做题少

思路就是左右两个指针从k位置开始去遍历，找最大的分数

class Solution {
public:
    int maximumScore(vector<int>& nums, int k) {
        int l = k,r = k,res = -1,n = nums.size();
        while(true){
            //从k的左右开始循环找，直到找到第一个比当前nums[k]小的停止 作为以当前nums[k]为核心的子数组的最大分数
            while(r < n && nums[r] >= nums[k])  r++;
            while(l >= 0 && nums[l] >= nums[k]) l--;
            //判断分数大小
            res = max(res,(r-l-1) * nums[k]);
            if(l < 0 && r >= n)  break;
            //主要是为了杜绝出现 3 5 3 3 3 3 3 3 3 3 3 3 初始k为5的位置，这样如果不匹配边上更小的情况可能不合理
            //防治两边出现数字小但是相对长度更大的情况
            if(l >= 0 && r < n) nums[k] = max(nums[l],nums[r]);
            else if(l < 0)  nums[k] = nums[r];
            else    nums[k] = nums[l];
        }
        return res;
    }
};