题解：CF997A Convert to Ones

题意

给定一个长度为 \(n\) 的01字符串，有以下两种操作：

1. 将一个子串翻转，花费 \(X\)
2. 将一个子串进行取反，花费 \(Y\)

求把原字符串变为全是 \(1\) 的字符串的最小代价。

思路

只有 \(2\) 操作的情况下

贪心策略。考虑到任意范围取反的花费相同，我们可以将相同的部分合并，如下图

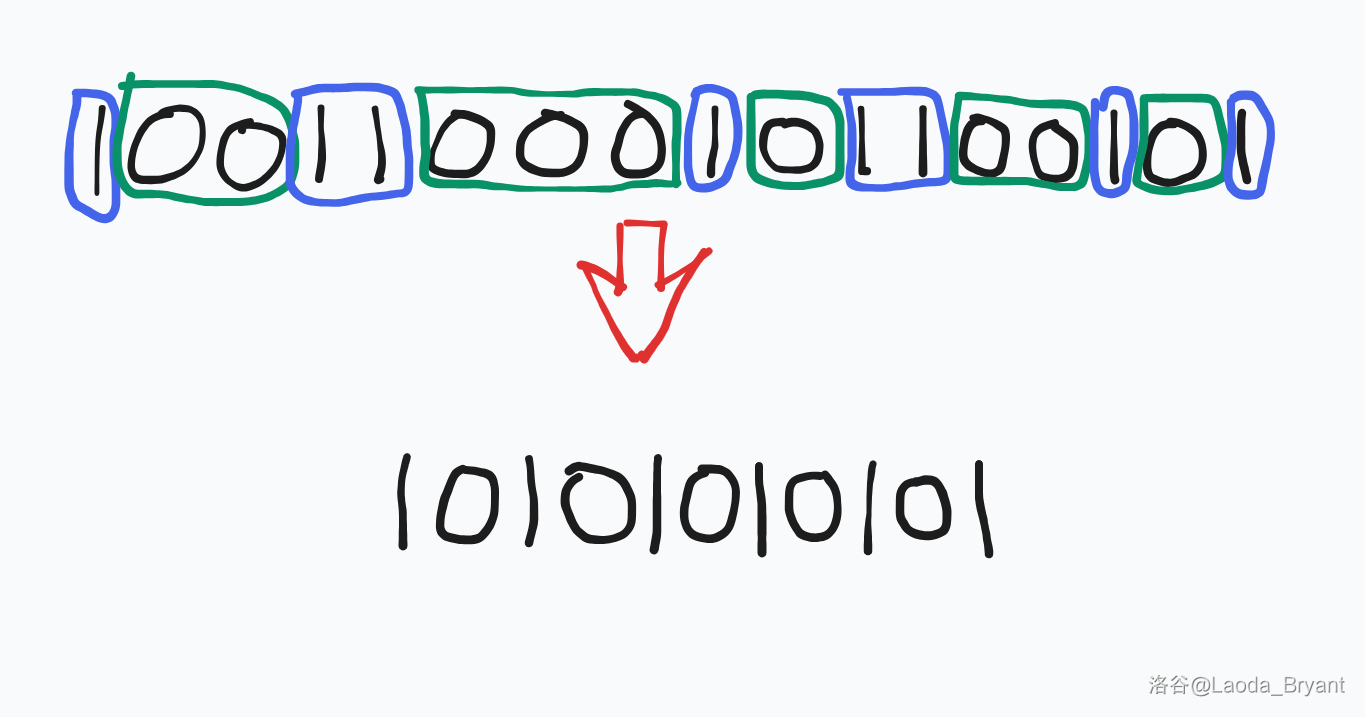
合并以后，会形成一个如 \(101010\dots\) 一样的字符串，每个 \(0\) 和 \(1\) 代表一个区间。此时，每个 \(0\) 代表一次操作。如果有 \(K\) 个 \(0\),那么总共花费为 \(K \times Y\)。

有 \(1\) 操作

刚刚的方法并不能保证是最小花费。
执行 \(1\) 操作，将其中的一个 \(1\) 和 \(0\) 进行翻转后，如下图

把相同的合并

就在刚刚的操作中减少了一个 \(0\)，这相当于把一个 \(0\) 直接取反

所以，一个 \(1\) 操作和一个 \(2\) 操作本质上是相同的。
当然，执行到最后只剩下一个 \(0\) 时，必须使用一次 \(2\) 操作，使原字符串全部为 \(1\)。
得本题的答案为
设：原字符串中有 \(k\) 段 \(0\)，\(A\) 和 \(B\) 代表操作 \(1\) 和 \(2\)

\[\min(A,B)\times(k-1)+B \]

AC code

#include<bits/stdc++.h>
using namespace std;
string s;
long long n,x,y,sum=0;
int main(){
	cin>>n>>x>>y;
	cin>>s;
	s[n]='1';
	for(int i=0;i<n;i++){
		if(s[i]=='0'&&s[i+1]=='1') sum++;
	}
	if(sum==0) cout<<0;
	else cout<<(sum-1)*min(x,y)+y;
	return 0;
}

注意

要开 long long，如果没有原字符串中没有 \(0\)，则直接输出 \(0\)。