BUAA_OO 第一单元总结

BUAA_OO 第一单元总结

一、程序结构

1. 第一次作业

作业任务：

• 识别多项式函数，并将其求导

• 不需进行格式检查

• 性能分由输出长度决定

代码思路：

　　在完成第一次作业时，由于对 java 面向对象的思想还不够了解，采用的代码架构还是类似于面向过程的编程 —— 通过正则表达式严格的依照给定的格式进行匹配。

度量分析：

　　程序类图如下：

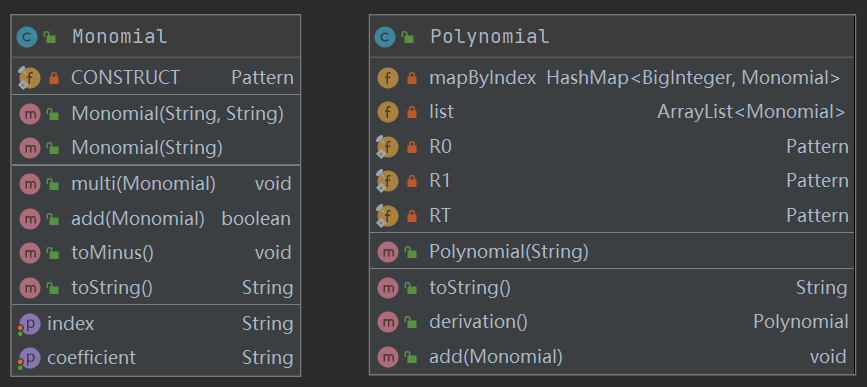
　　由于多项式的组成较为简单，所以我只构造了两个类，项（Monomial）和 多项式（Polynomial）

　　其中 Monomial 为多项式中的一个项，其中包括了相乘，相加，乘负一和 toString 方法.

　　Polynomial 为整个多项式，其中使用一个 HashMap 来存放各个项，包含了 加法、求导和 toString 方法。

　　使用 Metrics Reload 工具对代码进行分析得到：

　　注意到，本次作业的代码中，`Monomial 和 Polynomial 两个类的构造方法的各种复杂度都较高，这是由于其中大量使用了正则表达式对输入的字符来进行判断，采用了大量循环和判断语句。

这样的操作十分不利于代码的可拓展性，我也在进行第二次作业时对代码进行了重构 (重写)

2. 第二次作业

作业要求：

• 识别带有 三角函数因子、幂函数因子、表达式因子、常量因子 的多项式

• 不需进行格式检查

• 性能分由输出长度决定

代码思路：

　　吸取了上次的教训，这次的作业，我采用了 递归下降语法分析 来架构我的代码，通过 Parser 类来统一生产表达式，减少了各个类构造函数的复杂度。

度量分析：

　　程序类图如下：

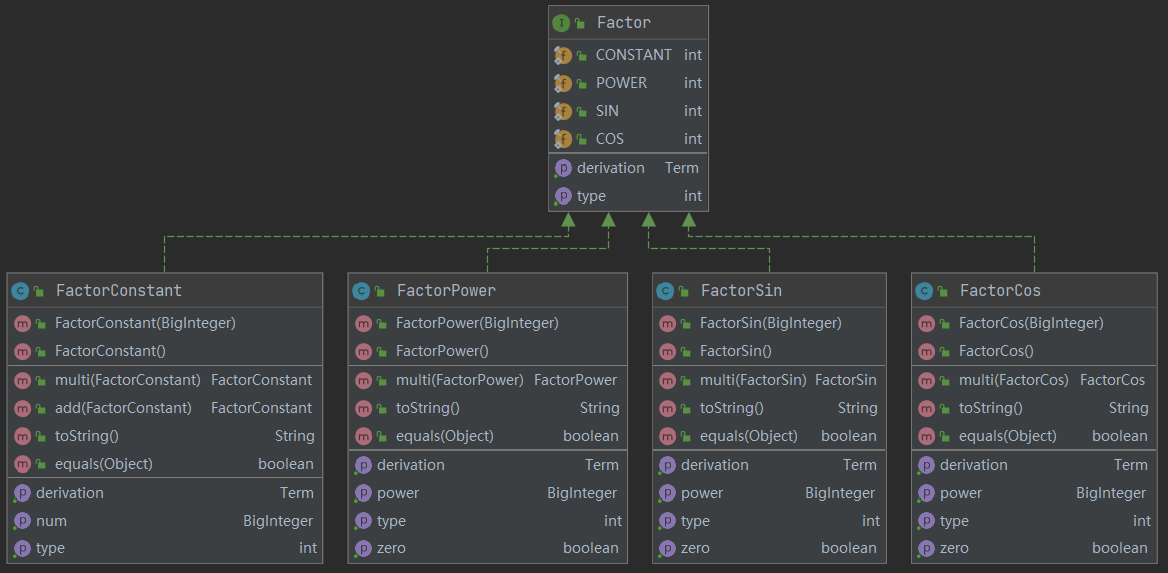
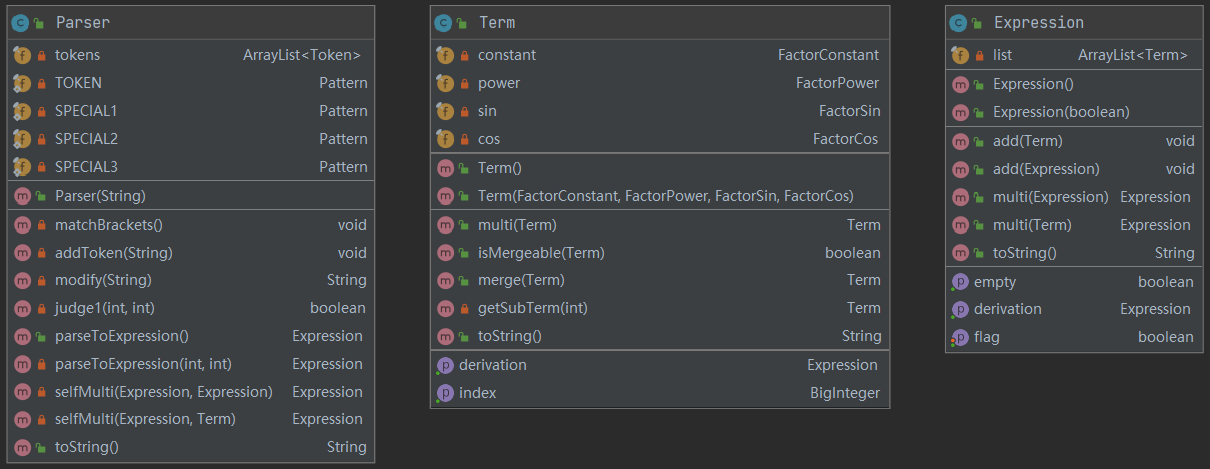
　　其中，常数因子、幂函数因子、两种三角函数因子都实现了 Factor 接口。这样设计的初衷是希望在 Term 类中可以统一的管理各个因子。但是后来，由于化简表达式的需要，我还是将各种因子分立的存放于 Term 类中了。

　　各个因子都有 相乘和 toString , equals 方法，Term 中还新增了“合并”方法。

　　最后在 Parser 类中，主要通过 构造函数 对输入进行了词法分析，在通过 parseToExpression 来对表达式进行解析。

　　使用 Metrics Reload 工具对代码进行分析得到：

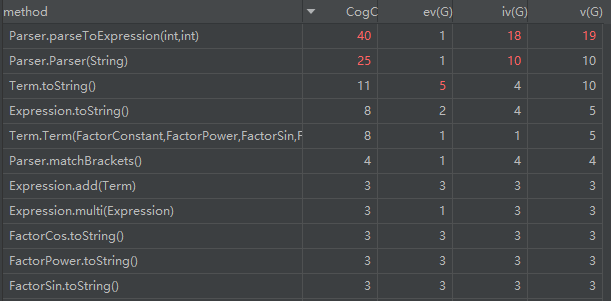
　　注意到，上述的方法中，Parser 的构造方法和 parserToExpression 方法的各项复杂度都很高，这是由于在构造函数中我多余的对括号的匹配与否进行了检查，而 parserToExpression 方法则以一己之力实现了本应由多个函数来实现的功能。

　　这些问题都在第三次作业中得到了修正。

3. 第三次作业

作业要求：

• 本次作业在上次的基础上增加了三角函数中可以嵌套其他因子的规则

• 本次作业 需要 进行格式检查，如果格式不正确，输出 “Wrong Format!”

• 性能分由输出长度决定

代码思路：

　　本次作业中，我将建立了 Derivable 接口，所有用来构建表达式的类全部实现了该接口，使得各个类可以被统一管理。

　　此外，本次的 解析器 中，不再通过一个方法来进行全部表达式的解析，而是对每个层次分别构造解析函数，降低了每个方法的复杂度，增加了代码的可读性。

度量分析：

　　程序类图如下：

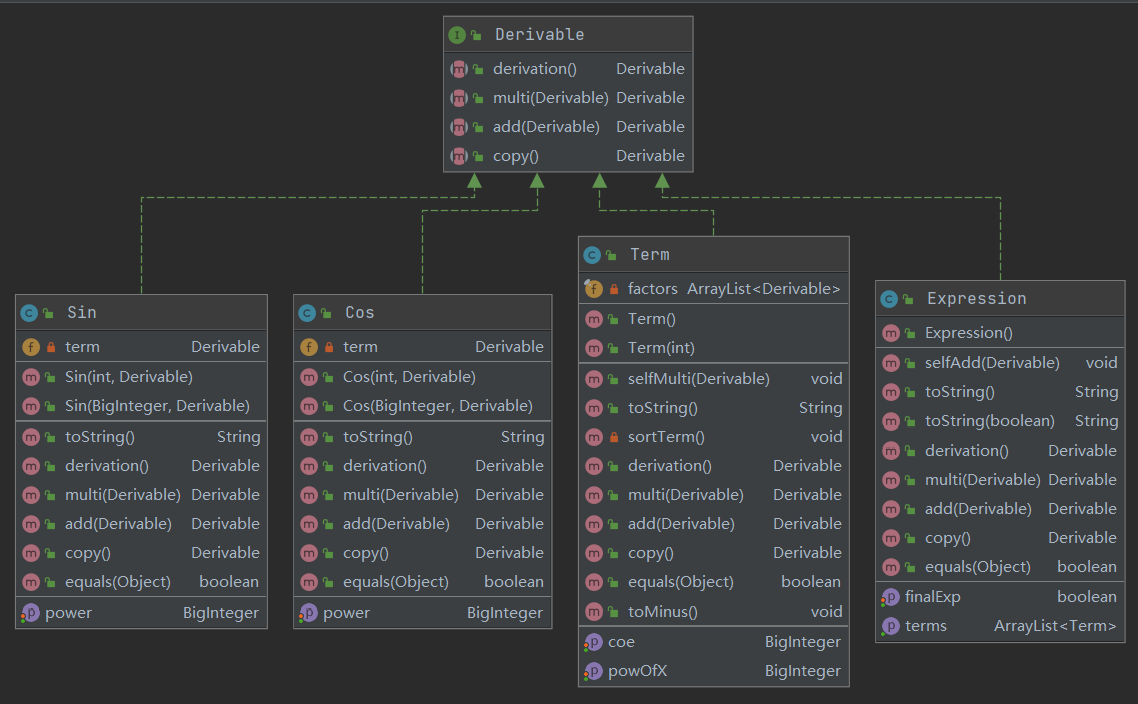
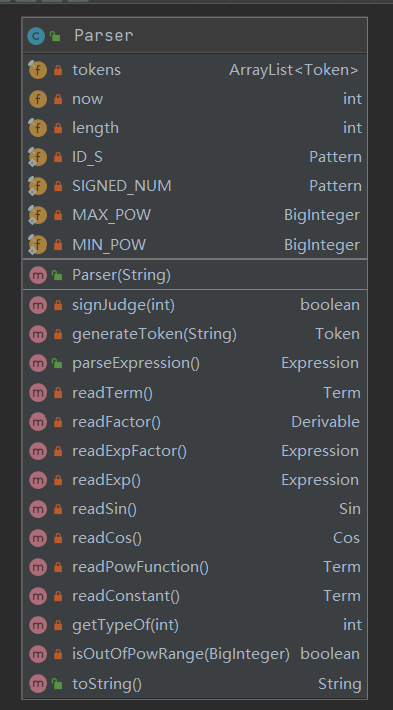
　　如上图所示，我分别建立了 sin, cos, term, expression 这4个类，并且将幂函数和常数因子合并到了 term 类中，便于合并同类项的处理。

　　而解析器中，依据层次的划分，分别建立了 readExp(), readTerm(), readFactor()三个解析函数，其中 readFactor() 方法又会根据当前标示符来选择调用 readSin(), readCos(), readConstant(), readPowFunction(), readExpFactor() 中的一个，或抛出 WrongFormatException

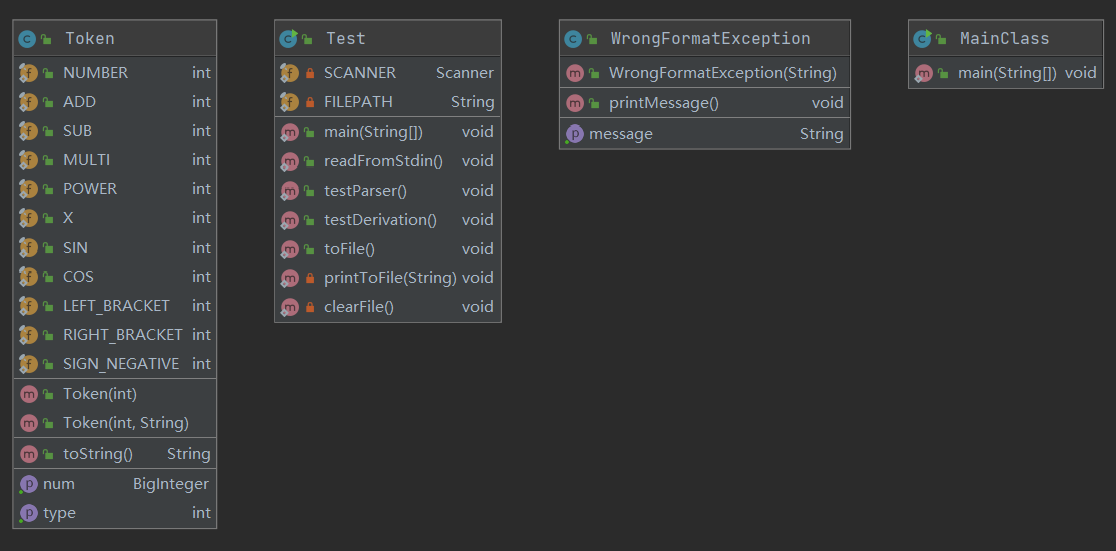
　　以上类均为辅助类或测试类，对功能的实现影响不大。

　　使用 Metrics Reload 工具对代码进行分析得到：

　　可以看到，此次作业中解析器中的函数的各项复杂度较为均衡，不想上次作业中某两个方法复杂度其高，而其他的较低。

　　较为复杂的方法还有 Term 类中的 toString() 方法，和 selfMulti() 方法。我认为主要原因是 Term 类中包含的因子种类众多，在转化为字符串时，需要进行多种优化，而在进行乘法时，需要判断传入的类的具体类型，均使用了大量的判断语句，造成了复杂度很高。

二、Bug 分析

1. 第二次作业

bug 成因：

　　在第二次作业中，我在互测阶段被 hack 出了一个 bug：

　　在建立新的 Expression 实例 e 后，e 为空，应该为零。

　　但是在读入时，我希望能将第一项乘在 e 上，故我设定当 e 为空时，将新的项加到 e 而不是乘到 e 上。

　　这导致如果发生 e 乘 0 或 在 e 合并同类项后为 0 ，则 e 也变为空，使下一次乘法被判定为加法。

　　这会导致将 (x - x) * x 被识别为 x 而不是 0

修改方式：

　　在创建 expression 时，添加一个 标志位，在刚刚创建时，标志位为 true ，在对该 expression 进行一次修改后，将标志位置为 false

2. 第三次作业

bug 成因：

　　在此次作业中，我被 hack 出了一个很愚蠢的 bug：

　　在词法分析时，只处理了标识符前的空白符，导致如果在行末存在任何空白符，都会导致词法分析器抛出 WrongFormatException

修改方式

　　对输入的字符串 line 调用 trim 方法，去掉行末的空白符。

三、测试策略

　　本次作业中我没有能成果 hack 到别人。

　　我测试别人和自己代码的方式主要是通过搭建的自动测评机来生成随机样例来进行测试。

　　而据我观察，房间中被人找出的 bug 绝大多数都是在进行 合并同类项、三角化简时出现的。实际上，随机生成的样例对这些情况的检查能力不强。在下次作业的互测过程中，我会尽量通过手动构造样例来覆盖更多的可能情况。

四、重构经历

　　本次作业中，我经历了两次重构。

第一次重构

　　本次重构中是将原本基于正则表达式的输入解析转化为了基于递归下降分析的输入解析。

　　对比两次的度量分析：

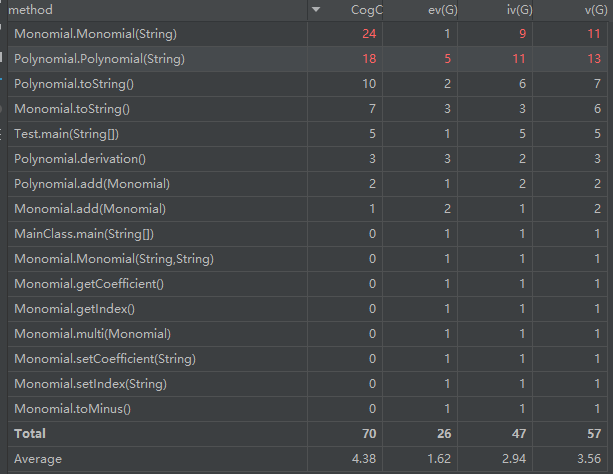
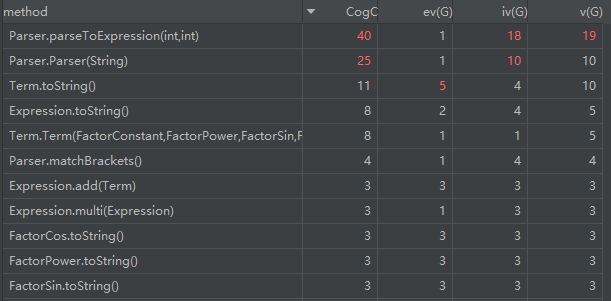
　　我们可以注意到，在第二次作业中，各种方法的复杂度不仅没有下降，反而还上升了，这种现象在当时没有引起我的注意，但是它对代码可拓展性造成了很大的影响，直接导致了第二次重构。

第二次重构

　　本次重构我主要进行了如下优化：

• 建立了 Derivable 接口来统一管理所有盛放了表达式的类

• 将常数因子和幂函数因子合并到了 项 中，因为这两个因子只有指数位是有信息的，如此处理可以便于合并同类项的化简。

• 将解析输入的函数按照我构造的数据结构的层次来进行了划分，将原本复杂的解析函数化简为了若干个简短、功能单一的函数，极大的增强了可拓展性（但是不会有下次作业了）

  对比重构前后的度量分析：

  

  

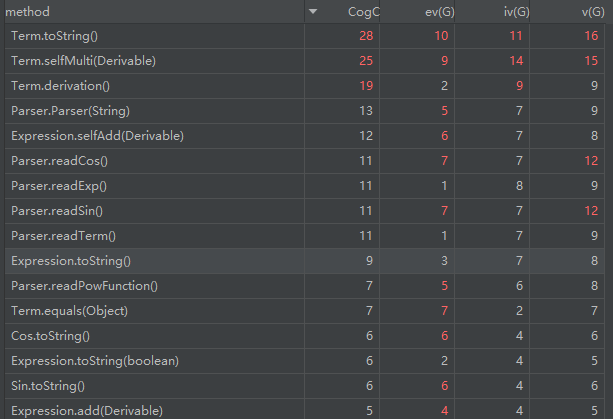
  可以发现虽然由于第三次作业对功能的要求变高导致了代码的整体复杂度上升了，但是单个函数的复杂度却下降了很多，尤其是解析表达式的 parserToExpression() 方法从顶部下降到了看不到的地方。

五、心得体会

　　通过本单元的学习，我学习到了如下几点：

• 对于有相似功能的几个类，建立接口来进行统一管理很有必要。

• 终日而思，不如须臾之所学。不要闭门造车，应该多关注课程平台的讨论区可以从各位 dalao 哪里学习到很多。本次作业中采用的 递归下降语法分析 就是从评论区的助教和 dalao 那里学习而来的。

• 先动脑再动手，在最初下手前，要给之后的自己留下充分的改进空间，千万不要前面挖坑，后面重构（或者甚至重写）

• 尽量减小每个方法的复杂度，最好每个方法完成且仅完成一个完整的功能。