网络流
P3376 【模板】网络最大流
思路
最大流,通过搜索在残量网络上找到增广路实现,同时要建反边,进行反悔操作。
重点说明建反边和反悔操作,反边的权值为容量减去正边的权值,所以找到这条反边存在的增广路相当于退流操作。
有两种实现方式:EK 和 Dinic。
代码
EK
点击查看代码
#include<iostream>
#include<cstring>
#include<climits>
#define int long long
using namespace std;
inline int read(){register int x = 0, f = 1;register char c = getchar();while (c < '0' || c > '9'){if (c == '-') f = -1;c = getchar();}while (c >= '0' && c <= '9'){x = (x << 1) + (x << 3) + (c ^ 48);c = getchar();}return x * f;}
inline void write(int x){if (x < 0) putchar('-'), x = -x;if (x > 9) write(x / 10);putchar(x % 10 + '0');}
int n, m, s, t, ans;
const int N = 210, M = 5e3 + 10;
int val[N][N];
struct edge{
int v, nxt, w;
}e[M << 1];
int head[N], cnt = 1;
void add(int u, int v, int w){
e[++cnt] = (edge){v, head[u], w};
head[u] = cnt;
}
bool vis[N];
int q[N], pre[N], g[N];
bool bfs(){
memset(vis, 0, sizeof vis);
memset(q, 0, sizeof q);
int h = 0, tail = 1;
q[1] = s;
vis[s] = 1;
g[s] = LLONG_MAX;
while (h <= tail){
h++;
for (int i = head[q[h]]; i; i = e[i].nxt){
int v = e[i].v;
if (vis[v] || e[i].w == 0) continue;
q[++tail] = v;
vis[v] = 1;
g[v] = min(g[q[h]], e[i].w);
pre[v] = i;
if (v == t) return 1;
}
}
return 0;
}
void update(){
int x = t;
while (x != s){
int l = pre[x];
e[l].w -= g[t];
e[l ^ 1].w += g[t];
x = e[l ^ 1].v;
}
ans += g[t];
}
signed main(){
n = read(), m = read(), s = read(), t = read();
for (int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
val[u][v] += w;
}
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++){
if (val[i][j]) add(i, j, val[i][j]), add(j, i, 0);
}
}
while (bfs()) update();
cout << ans;
return 0;
}
Dinic
点击查看代码
#include<iostream>
#include<climits>
#include<queue>
#define int long long
using namespace std;
inline int read(){register int x = 0, f = 1;register char c = getchar();while (c < '0' || c > '9'){if (c == '-') f = -1;c = getchar();}while (c >= '0' && c <= '9'){x = (x << 1) + (x << 3) + (c ^ 48);c = getchar();}return x * f;}
inline void write(int x){if (x < 0) putchar('-'), x = -x;if (x > 9) write(x / 10);putchar(x % 10 + '0');}
const int N = 1e3 + 10, M = 5e3 + 10, INF = LONG_LONG_MAX;
int n, m, s, t, ans;
struct edge{
int v, w, nxt;
}e[M << 1];
int head[N], cur[N], cnt = 1;
void add(int u, int v, int w){
e[++cnt] = (edge){v, w, head[u]};
head[u] = cnt;
}
int dep[N];
bool bfs(){
queue<int> q;
for (int i = 1; i <= n; i++){
dep[i] = INF;
}
q.push(s);
dep[s] = 0;
while (!q.empty()){
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt){
int v = e[i].v;
if (dep[v] != INF || e[i].w <= 0) continue;
q.push(v);
dep[v] = dep[u] + 1;
if (v == t) return 1;
}
}
return 0;
}
int dfs(int u, int sum){
if (u == t) return sum;
int res = 0;
for (int i = cur[u]; i; i = e[i].nxt){
cur[u] = i;
int v = e[i].v;
if (dep[v] != dep[u] + 1 || e[i].w <= 0) continue;
int s = dfs(v, min(sum, e[i].w));
e[i].w -= s;
e[i ^ 1].w += s;
res += s;
sum -= s;
if (sum == 0) return res;
}
return res;
}
signed main(){
n = read(), m = read(), s = read(), t = read();
for (int i = 1; i <= m; i++){
int u = read(), v = read(), w = read();
add(u, v, w), add(v, u, 0);
}
while (bfs()){
for (int i = 1; i <= n; i++) cur[i] = head[i];
ans += dfs(s, INF);
}
cout << ans;
return 0;
}
P1402 酒店之王
思路
一眼网络流,但是难点在建图,显然,可以每个房间向人连,每个人向菜连,但是,一个点没有权,可能会走很多次,数量不对,这是将人这个点拆开,分成两个点,中间边权为 \(1\),这样就可以避免一个人被走很多次。
代码
点击查看代码
#include<iostream>
#include<climits>
#include<queue>
#define int long long
using namespace std;
inline int read(){register int x = 0, f = 1;register char c = getchar();while (c < '0' || c > '9'){if (c == '-') f = -1;c = getchar();}while (c >= '0' && c <= '9'){x = (x << 1) + (x << 3) + (c ^ 48);c = getchar();}return x * f;}
inline void write(int x){if (x < 0) putchar('-'), x = -x;if (x > 9) write(x / 10);putchar(x % 10 + '0');}
const int N = 1e3 + 10, M = 1e4 + 10, INF = LONG_LONG_MAX;
int n, p, q, ans;
struct edge{
int v, w, nxt;
}e[M << 1];
int head[N], cur[N], cnt = 1;
void add(int u, int v, int w){
e[++cnt] = (edge){v, w, head[u]};
head[u] = cnt;
}
int dep[N];
bool bfs(){
queue<int> q;
for (int i = 0; i <= 500; i++){
dep[i] = INF;
}
q.push(0);
dep[0] = 0;
while (!q.empty()){
int u = q.front();
q.pop();
for (int i = head[u]; i; i = e[i].nxt){
int v = e[i].v;
if (dep[v] != INF || e[i].w <= 0) continue;
q.push(v);
dep[v] = dep[u] + 1;
if (v == 500) return 1;
}
}
return 0;
}
int dfs(int u, int sum){
if (u == 500) return sum;
int res = 0;
for (int i = cur[u]; i; i = e[i].nxt){
cur[u] = i;
int v = e[i].v;
if (dep[v] != dep[u] + 1 || e[i].w <= 0) continue;
int s = dfs(v, min(sum, e[i].w));
e[i].w -= s;
e[i ^ 1].w += s;
res += s;
sum -= s;
if (sum == 0) return res;
}
return res;
}
signed main(){
n = read(), p = read(), q = read();
for (int i = 1; i <= p; i++) add(0, i + n * 2, 1), add(i + n * 2, 0, 0);
for (int i = 1; i <= n; i++) add(i, i + n, 1), add(i + n, i, 0);
for (int i = 1; i <= q; i++) add(i + n * 2 + p, 500, 1), add(500, i + n * 2 + p, 0);
for (int i = 1; i <= n; i++){
for (int j = 1; j <= p; j++){
bool a = read();
if (a) add(j + n * 2, i, 1), add(i, j + n * 2, 0);
}
}
for (int i = 1; i <= n; i++){
for (int j = 1; j <= q; j++){
bool a = read();
if (a) add(i + n, j + n * 2 + p, 1), add(j + n * 2 + p, i + n, 0);
}
}
while (bfs()){
for (int i = 0; i <= 500; i++) cur[i] = head[i];
ans += dfs(0, INF);
}
cout << ans;
return 0;
}
[ARC125E] Snack
思路
看到这道题,很容易想到最大流,建边也很好想,如下图:
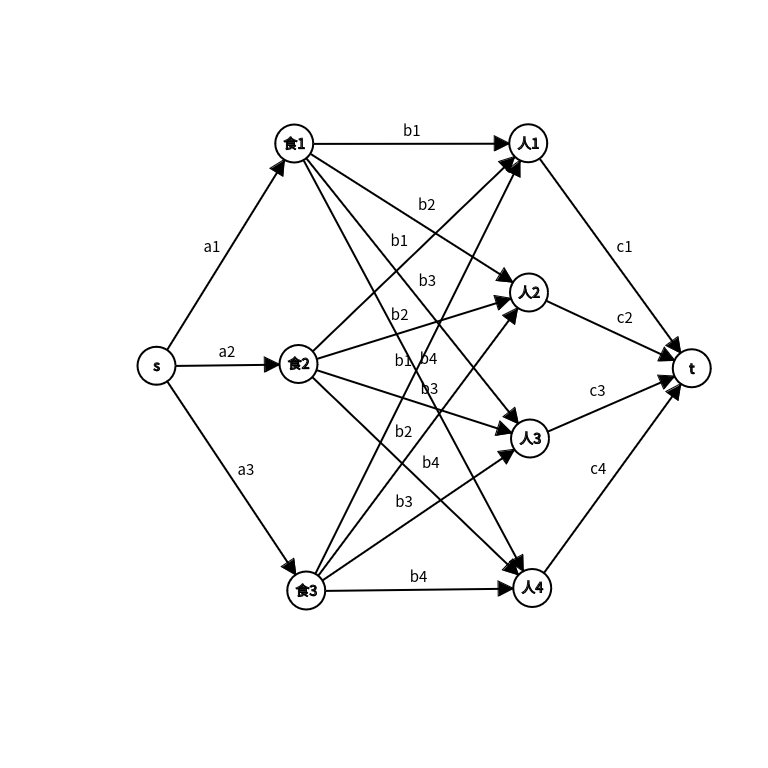
但是,建这么多的边会有问题,就是时间复杂度太高,跑不了网络流,所以我们换一种思路。
有一个重要的结论就是:最大流 \(=\) 最小割
证明可以看这里,这里不证明了。
于是题目就转化为了对于上面这张图求最小割。
我们发现,我们要割掉左边一些零食点集与 \(s\) 的连边,同理割掉右边一些人的点集与 \(t\) 的边,再割掉中间某些 \(b_i\) 的边。
我们可以将这个过程看成删掉左右两边某些点,再删掉中间的某些边,有一个非常妙的性质就是,删掉左右两边的某些点后,必须将没删掉的那些点之间的所有连边全部删除才能保证图不联通,因为对于每一个零食,都对每个人连了边。
设左边零食删去的点集为 \(A\), 右边人删去的点集为 \(c\),那么答案就为下面式子的最小值:
\(|A|\) 表示 \(A\) 集合的大小。
进一步地,我们将式子后面的两坨改一下,变为求下面式子的最小值:
让我们感性理解一下,左边为删掉某些零食点集的贡献,右边为选枚举人的点集中的所有点,要么删掉这个人,要么删掉左边剩余零食点集与这个人的所有 \(b_i\) 的边,由于要求最小割,所以取两者中的最小值保证图不联通。
于是题目就变为快速求上面这个式子。
首先我们枚举 \(A\) 集合的大小,在当前大小下,肯定选择的点是 \(s\) 与之连边 \(a_i\) 最小的几个,于是先对 \(a_i\) 排序。
如何快速求式子右边那一坨,将 \(\frac{c_i}{b_i}\) 求出来,设 \(x_i = \frac{c_i}{b_i}\),这样当 \(n-|A|=x_i\) 时,\(b_i(n-|A|)=c_i\),\(n-|A|<x_i\) 时取 \(b_i(n-|A|)\),\(n-|A|>x_i\) 时取 \(c_i\)(当然 \(x_i\) 可能为小数,可以将 \(x_i+1\) 向下取整,看到后面就明白了)。
接下来思路就很明确了,每次枚举到一个 \(n-|A|\),后面那个式子有些保持不变,有些超过了临界点,改变了数值,所以以 \(x_i\) 为第一关键字从小到大排序,求出 \(b_i\) 与 \(c_i\) 的前缀和,每次二分大于等于 \(n-|A|\) 的 \(x_i\) 的位置,前面的还是 \(b_i(n-|A|)\),后面的是 \(c_i\),利用前缀和统计答案(这时 \(x_i+1\) 就有用了,因为浮点数范围太小,\(x_i+1\) 后二分到这个临界点随便取 \(b_i\) 还是 \(c_i\) 都是同样的结果)。
代码
点击查看代码
#include<iostream>
#include<algorithm>
#include<climits>
#define int long long
using namespace std;
inline int read(){register int x = 0, f = 1;register char c = getchar();while (c < '0' || c > '9'){if (c == '-') f = -1;c = getchar();}while (c >= '0' && c <= '9'){x = (x << 1) + (x << 3) + (c ^ 48);c = getchar();}return x * f;}
inline void write(int x){if (x < 0) putchar('-'), x = -x;if (x > 9) write(x / 10);putchar(x % 10 + '0');}
const int N = 2e5 + 10;
int n, m, sum, ans = LONG_LONG_MAX;
int a[N], qc[N], qb[N];
struct node{
int x, b, c;
bool operator < (const node &w) const{
return x < w.x;
}
}p[N];
signed main(){
n = read(), m = read();
for (int i = 1; i <= n; i++) a[i] = read();
for (int i = 1; i <= m; i++) p[i].b = read();
for (int i = 1; i <= m; i++) p[i].c = read();
for (int i = 1; i <= m; i++) p[i].x = p[i].c / p[i].b + 1;
sort(a + 1, a + n + 1);
sort(p + 1, p + m + 1);
for (int i = 1; i <= m; i++) qc[i] = qc[i - 1] + p[i].c, qb[i] = qb[i - 1] + p[i].b;
for (int i = 0; i <= n; i++){
sum += a[i];
int y = n - i;
int l = 1, r = m;
while (l <= r){
int mid = (l + r) >> 1;
if (y >= p[mid].x){
l = mid + 1;
}else{
r = mid - 1;
}
}
ans = min(ans, sum + qc[r] + (qb[m] - qb[r]) * y);
}
cout << ans;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号