什么是动态规划（Dynamic Programming, DP）

动态规划（DP） 是一种用于最优化问题的算法设计方法，它通过拆解子问题、存储子问题解，避免重复计算，从而提高效率。

动态规划的核心思想

1. 最优子结构（Optimal Substructure）
   • 一个问题的最优解可以由其子问题的最优解推导出来。
2. 重叠子问题（Overlapping Subproblems）
   • 计算同一个子问题时会多次出现相同的计算，DP 通过存储这些子问题的解来避免重复计算。
3. 状态转移方程（Recurrence Relation）
   • 定义一个递推公式，让问题可以从小规模推导到大规模。

区别于贪心算法：

• 贪心算法：每一步选择当前最优，不能回溯，可能得不到全局最优解。
• 动态规划：会记录之前的计算结果，并基于子问题的最优解来构造整体最优解。

C# 示例：使用动态规划求解斐波那契数列

问题描述

计算斐波那契数列 F(n)，其中：

F(n)=F(n−1)+F(n−2)

且

F(0)=0, F(1)=1

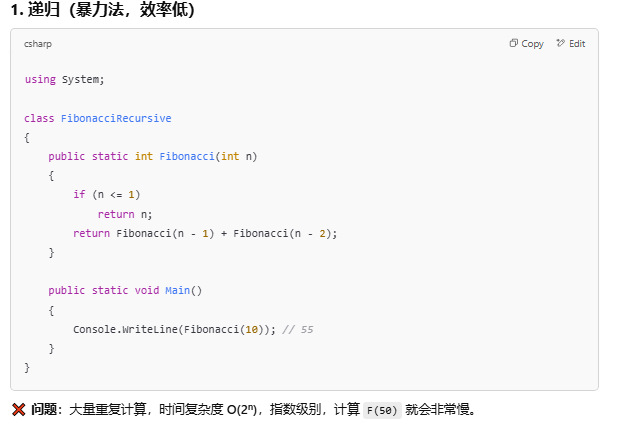
1. 递归（暴力法，效率低）

 

 

 

 

总结

方法	时间复杂度	空间复杂度	适用场景
递归（暴力）	O(2ⁿ)	O(n)	只适合小 n
记忆化搜索	O(n)	O(n)	适合递归场景
动态规划（数组）	O(n)	O(n)	适合 n 较大的情况
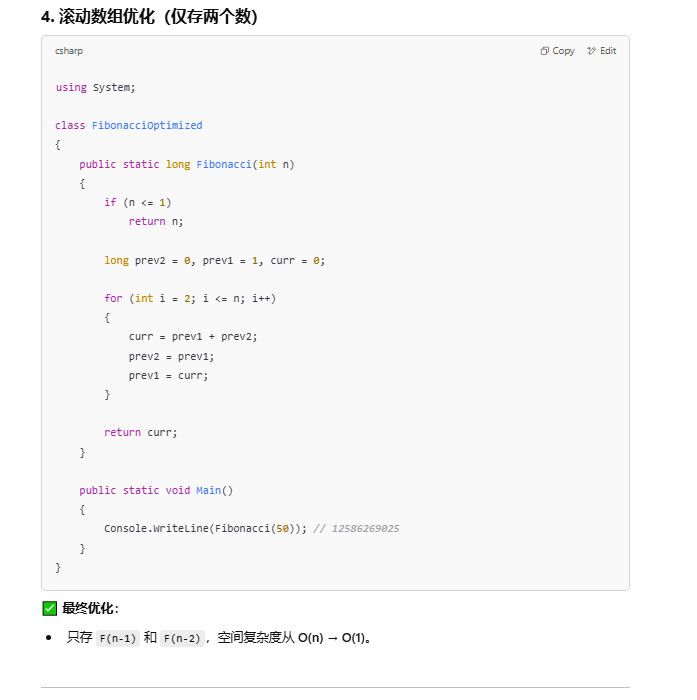
滚动数组优化	O(n)	O(1)	最优解

 

 

🚀 动态规划本质是对递归的优化，避免重复计算，提高效率，适用于最优化问题，如背包问题、最长公共子序列等！