一、二叉搜索树(BSTree)的概念
二叉搜索树又被称为二叉排序树,那么它本身也是一棵二叉树,那么满足以下性质的二叉树就是二叉搜索树:
1、若左子树不为空,则左子树上左右节点的值都小于根节点的值
2、若它的右子树不为空,则它的右子树上所有的节点的值都大于根节点的值
3、它的左右子树也要分别是二叉搜索树
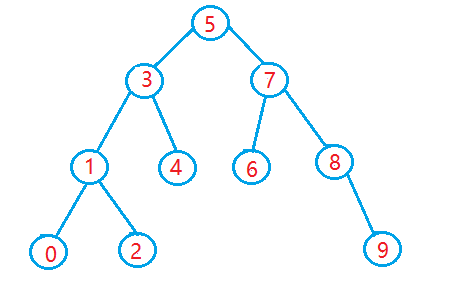
===================================================================
二、二叉搜索树的插入
1、搜索
插入之前我们先来说说它的搜索,像上图这样的一棵二叉搜索树,我们要查找某一个元素是很简单的。因为它的节点分布是有规律的,所以查找一棵元素只需要如下的步骤就可以了:

2、插入
由于二叉搜索树的特殊性质确定了二叉搜索树中每个元素只可能出现一次,所以在插入的过程中如果发现这个元素已经存在于二叉搜索树中,就不进行插入。
否则就查找合适的位置进行插入。
第一种情况:_root为空
直接插入,return true;
第二种情况:要插入的元素已经存在
如上面所说,如果在二叉搜索树中已经存在该元素,则不再进行插入,直接return false;
第三种情况:能够找到合适位置
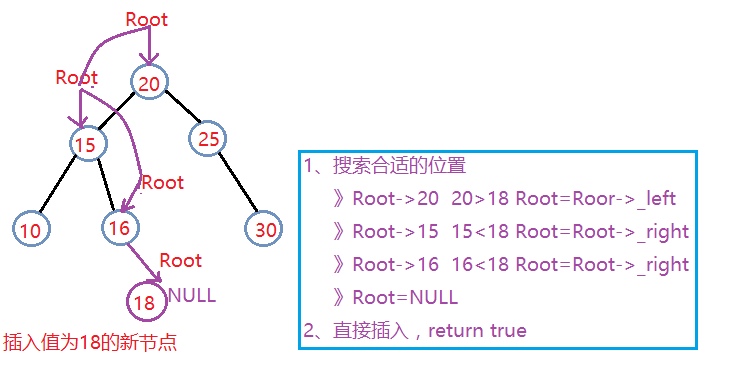
===================================================================
三、二叉搜索树的删除
对于二叉搜索树的删除操作,主要是要理解其中的几种情况,写起来还是比较简单的。
当然一开始还是需要判断要删除的节点是否存在于我们的树中,如果要删除的元素都不在树中,就直接返回false;否则,再分为以下四种情况来进行分析:
》要删除的节点无左右孩子
》要删除的节点只有左孩子
》要删除的节点只有右孩子
》要删除的节点有左、右孩子
删除方法解释:
对于第一种情况,我们完全可以把它归为第二或者第三种情况,就不用再单独写一部分代码进行处理;
》如果要删除的节点只有左孩子,那么就让该节点的父亲结点指向该节点的左孩子,然后删除该节点,返回true;
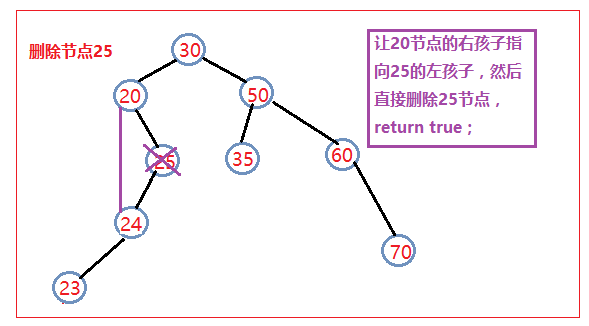
》如果要删除的节点只有右孩子,那么就让该节点的父亲结点指向该节点的右孩子,然后删除该节点,返回true;
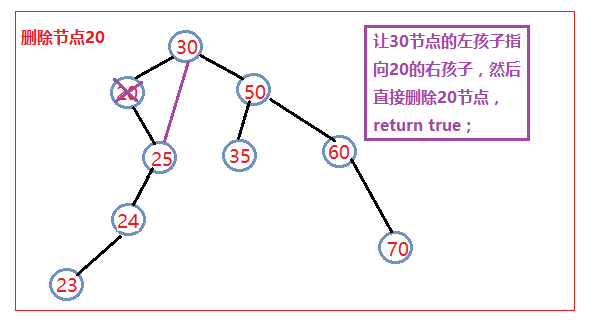
对于上面这两种情况我们还应该在之前进行一个判断,就是判断这个节点是否是根节点,如果是根节点的话,就直接让根节点指向这个节点的左孩子或右孩子,然后删除这个节点。
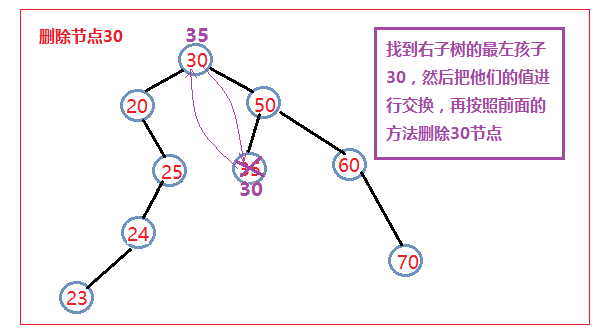
》最后一种也是最麻烦的一种就是要删除的节点的左右孩子都存在。此时我们的删除方法如下:
1、找到该节点的右子树中的最左孩子(也就是右子树中序遍历的第一个节点)
2、把它的值和要删除的节点的值进行交换
3、然后删除这个节点即相当于把我们想删除的节点删除了,返回true;
===================================================================
程序代码:
1、二叉搜索树的插入操作
1 bool Insert(const K& key)
2 {
3 if (_root == NULL)
4 {
5 _root = new Node(key);
6 return true;
7 }
8 Node* parent=NULL;
9 Node* pcur = _root;
10 while (pcur)
11 {
12 if (pcur->_key == key) //有key节点,则不再插入
13 return false;
14 if (pcur->_key > key)
15 {
16 parent = pcur;
17 pcur = pcur->_left;
18 }
19 else if (pcur->_key < key)
20 {
21 parent = pcur;
22 pcur = pcur->_right;
23 }
24 }
25 if (parent->_key < key)
26 parent->_right = new Node(key);
27 else
28 parent->_left = new Node(key);
29 return true;
30 }
2、二叉搜索树的删除操作 bool Remove(const K& key)
1 bool Remove(const K& key)
2 {
3 assert(_root);
4 Node* parent = NULL;
5 Node* pcur = _root;
6 Node* del = pcur;
7 while (pcur != NULL && pcur->_key != key)
8 {
9 if (pcur->_key > key)
10 {
11 parent = pcur;
12 pcur = pcur->_left;
13 }
14 else if (pcur->_key < key)
15 {
16 parent = pcur;
17 pcur = pcur->_right;
18 }
19 }
20 if (pcur == NULL)
21 return false;
22 if (pcur->_left == NULL) //只有右孩子
23 {
24 //如果pcur就是根节点的话,让根节点指向根的右
25 if (pcur == _root)
26 _root = pcur->_right;
27 else if (pcur == parent->_left)
28 {
29 parent->_left = pcur->_right;
30 }
31 else
32 {
33 parent->_right = pcur->_right;
34 }
35 del = pcur;
36 }
37 else if (pcur->_right == NULL) //只有左孩子
38 {
39 //如果是根节点,让根节点指向根的左
40 if (pcur == _root)
41 _root = pcur->_left;
42 else if (parent->_left == pcur)
43 {
44 parent->_left = pcur->_left;
45 }
46 else
47 parent->_right = pcur->_left;
48 del = pcur;
49 }
50 //pcur左右孩子都不为空
51 else
52 {
53 //找到节点右子树的最左节点
54 Node* left = pcur->_right;
55 parent = pcur;
56 while (left->_left)
57 {
58 parent=left;
59 left = left->_left;
60 }
61 del = left;
62 pcur->_key = left->_key; //交换节点的值
63 if (parent->_left == left)
64 {
65 parent->_left = left->_right;
66 }
67 else
68 {
69 parent->_right = left->_right;
70 }
71
72 }
73 delete del;
74 return true;
75 }





 浙公网安备 33010602011771号
浙公网安备 33010602011771号