算法学习-斐波那契数列(C#)

学习斐波那契，是因为面试的时候问起来的，一开始是让我手写一个斐波那契的算法实现，好久没写这玩意了，都忘了，于是在面试之后开始准备补充一点算法知识。

斐波那契的具体数学实现公式还是很简单的，F(n+1)=F(n)+F(n−1), n⩾3。

在学习的过程中参考了好几篇文章，主要是这篇文章对我的影响很大，基本上我都是按照这个文章去实现的。这篇文章的前两个实现斐波那契算法的代码都很简单，不难看懂，我主要是纠结在第三个，第三个牵扯到一个矩阵的数学概念。由于本人是个学渣，数学不行，所以不得不现在赶紧去补充一下知识。下面我简单的说一下研究第三个算法实现的学习过程吧！

首先需要了解矩阵，矩阵到底是用来干嘛的，这个其实很多地方都有说明，实在不行你去维基百科，或者百度百科，总会有你想要的概念。其实在看这些百科里的介绍的时候，我也是很头疼，因为我的数学基础实在是太薄弱了，我学习一个东西的时候，喜欢看一下这个东西的具体用处，然后再去理解它，喜欢从具体的层面去查看。所以我选择了一个最为快捷的办法，看视频，如果大家可以FQ可以从油管去查看，我是看了一个湾湾的大叔介绍的，还是很不错的，具体链接地址，除了这个之外我还看了一下矩阵的乘法，其实自我感觉不是很难，这个也是有很多地方可以搜索到的，我就不赘述了。其他国内的视频网站应该也有这个介绍，应该很多，我没有具体去验证。

如果你简单理解了矩阵，那其实就可以将刚才的数学公式推导成这样一个矩阵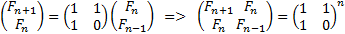，，为防止有同学和我一样不是很理解这个具体怎么推导的，我简单给出如下两个公式吧，大神请轻喷。

F(n+1) = F(n) + F(n-1)；F(n) = F(n)；看到这里怕是有很多人觉得我太笨了，是的，我确实很笨，哈哈哈哈哈。

有了上面的一个推导公式之后，不知道会不会有同学会跟我一开始一样，不知道怎么去实现这个算法，其实我看了一会上面说的第三个算法实现，我也迷茫了一会。但是其实仔细看一下那个矩阵的公式，就可以看出来，F(n)就是我们要的结果。有了这个信息再看看第三个算法的实现其实就一目了然了，第三个方式是使用二维数组来实现这个2阶矩阵。大家有兴趣的可以在自己的机器上敲一敲玩一下，反正代码很少，哈哈哈哈哈。

除此之外就是时间复杂度的一个说明，时间复杂度我之前一直也不是很了解，到底是一个什么概念（也不算完全不懂，只知道大概是一个算法效率时间上的度量方式，不知道对不对，哈哈哈哈）。后面FQ看了一个油管的一系列视频，链接地址，大概理解了，可以这么简单描述一下吧，依然是大神请轻喷。在计算一个算法的效率的时候，会有一系列的公式计算，然后假如有这么几种：

• 2n +3
• 2n^2 + 3
• n^3+n+100
• 2n^2+3n+1

以上几个公式其实可以简化成以下几种：

• n
• n^2
• n^3
• n^2

可能会有同学会问为什么。其实通过上面分享的视频可以知道（哦哦，有的同学可能不能FQ，(╯﹏╰)b），是因为随着n的增长，那些变化率较低的函数公式，例如第四个的3n+1与2n^2相比已经没有可比性了，所以也可以说这个复杂度其实就是将那些影响力最大的函数剥离出来，然后使用O（读作大O。。。。￣□￣｜｜）标记，于是乎便有了O(n)、O(n^2)、O(logN)这些时间复杂度的表示。