剑指offer（专项突击版）

剑指 Offer II 001. 整数除法

给定两个整数 a 和 b ，求它们的除法的商 a/b ，要求不得使用乘号 '*'、除号 '/' 以及求余符号 '%' 。

注意：

整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2
假设我们的环境只能存储 32 位有符号整数，其数值范围是 [−231, 231−1]。本题中，如果除法结果溢出，则返回 231 − 1

不可以使用除法和乘法，则可以使用加法或位运算。
因为限制了只能使用23位有符号整数，所以不能使用long。数的范围为\(-2^{31} 到 2^{31}-1\)。
先考虑特殊情况：
1. 当a为\(-2^{31}\),b为-1，则结果存在int32时的溢出情况，此时应返回\(2^{13}-1\)
2. 当a为0或b为1，则直接返回a
3. 剩余就是正常情况处理了；正常处理的时候，我们往往会先将符号位确定出来，然后全部当做正数去处理。这时候，存在一个陷阱：a为\(-2^{31}\)且b不为-1时，对a取绝对值，在java中存在溢出情况。那么，反之可以将其全部当做负数处理就不存在溢出情况了。
```
public int divide(int a, int b) {
        // 先考虑特殊情况
        // 考虑溢出情况：-2^31 ~ 2^31 -1
        // a=-2^31 b=-1 则出现上溢,返回2^31 -1
        if (a == Integer.MIN_VALUE && b == -1) {
            return Integer.MAX_VALUE;
        }
        // 被除数为0或除数为1
        if (a == 0 || b == 1) {
            return a;
        }

        // 考虑符号
        int flag = (a > 0) ^ (b > 0) ? -1 : 1;
        // 正常处理,有一个陷阱，对-2^31取绝对值存在溢出
        // 所以，反过来求值
        if(a>0) {a=-a;}
        if(b>0) {b=-b;}
        int res = 0;
        while (a<=b){
            a-=b;
            res++;
        }
        return flag*res;
    }
```
显然，这样是最简单的方法，还有优化的空间。那就是采用位运算。如下所示可以加速上边代码的while过程：

a=14 b=-2

Step1：flag = -1

Step2：a=-14 b=-2

Step3:

res = 0

round1：

base=1；dividor=-2；dividor=dividor<<2=-8; base=base<<2=4; a=a-dividor=-6; res=res+4=4;

round2：

base=1；dividor=-2；dividor=dividor<<1=-4; base=base<<1=2; a=a-dividor=-2; res=res+2=6;

round3：

base=1；dividor=-2；（此时while内部循环不执行，base为1） a=a-dividor=0; res=res+base=7;

// 显然divide有更进一步的优化方法
    public int divide1(int a, int b) {
        // 先考虑特殊情况
        // 考虑溢出情况：-2^31 ~ 2^31 -1
        // a=-2^31 b=-1 则出现上溢,返回2^31 -1
        if (a == Integer.MIN_VALUE && b == -1) {
            return Integer.MAX_VALUE;
        }
        // 被除数为0或除数为1
        if (a == 0 || b == 1) {
            return a;
        }

        // 考虑符号
        int flag = (a > 0) ^ (b > 0) ? -1 : 1;
        // 正常处理,有一个陷阱，对-2^31取绝对值存在溢出
        // 所以，反过来求值
        if(a>0) {a=-a;}
        if(b>0) {b=-b;}
        int res = 0;
        // 这里可以使用位运算加速
        while (a<=b){
            int base = 1;
            int dividor = b;
            while (a-dividor<=dividor){
                dividor<<=1;
                base<<=1;
            }
            a-=dividor;
            res+=base;
        }
        return flag*res;
    }

剑指 Offer II 002. 二进制加法

给定两个 01 字符串 a 和 b ，请计算它们的和，并以二进制字符串的形式输出。

输入为非空字符串且只包含数字 1 和 0。

输入: a = "1010", b = "1011"
输出: "10101”

每个字符串仅由字符 '0' 或 '1' 组成。

1 <= a.length, b.length <= 10^4

字符串如果不是 "0" ，就都不含前导零。

因为字符串的长度足够大，所以必须采用字符串解决，而不能将其转为10进制数字后求和再转为2进制处理。

思路1：简单模拟。逆序同步扫描字符，进行累加，后分别对2求余数的商来更新结果。如下,时间复杂度\(O(n)\)，空间复杂度\(O(1)\)。其中\(n=max(a.length(),b.length())\)。

public String addBinary(String a, String b) {
        int carry = 0;
        int n = Math.max(a.length(), b.length());
        StringBuffer stringBuffer = new StringBuffer();
        for (int i = 0; i < n; i++) {
            // 定位导数第i个元素，并累加
            carry += i < a.length() ? (a.charAt(a.length() - i - 1) - '0') : 0;
            carry += i < b.length() ? (b.charAt(b.length() - i - 1) - '0') : 0;
            stringBuffer.append((char) (carry % 2 + '0'));
            carry /= 2;
        }
        if(carry>0){
            stringBuffer.append('1');
        }
        stringBuffer.reverse();
        return stringBuffer.toString();
    }

剑指 Offer II 003. 前 n 个数字二进制中 1 的个数

给定一个非负整数 n ，请计算 0 到 n 之间的每个数字的二进制表示中 1 的个数，并输出一个数组。

输入: n = 2
输出: [0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10

思路1：分别对每一个数字进行位统计。2进制位1的个数，可以采用Brian Kernighan算法，其统计的时间复杂度为\(O(logn)\). 该算法是这样的：

令: \(x=x\&(x-1)\) ,该操作可以将x的二进制位的最后一个1置为0，当x为0的时候，x的二进制位中就没有1了。

该思路整体的时间复杂度为\(O(nlogn)\)。

public int[] countBits(int n) {
    int[] res = new int[n+1];
    for (int i = 0; i <= n; i++) {
        res[i] = getBits1(i);
    }
    return res;
}
private int getBits1(int i) {
    int count = 0;
    while (i>0){
        i = i&(i-1);
        count++;
    }
    return count;
}

思路2：动态规划；dp[i]表示i的二进制中1的个数，则有\(dp[i]=dp[i\&(i-1)]+1\)。该方法时间复杂度为\(O(n)\)。初识dp[0]=0;

public int[] countBits(int n) {
    int[] res = new int[n+1];
    for (int i = 1; i <= n; i++) {
        res[i] = res[i&(i-1)]+1;
    }
    return res;
}

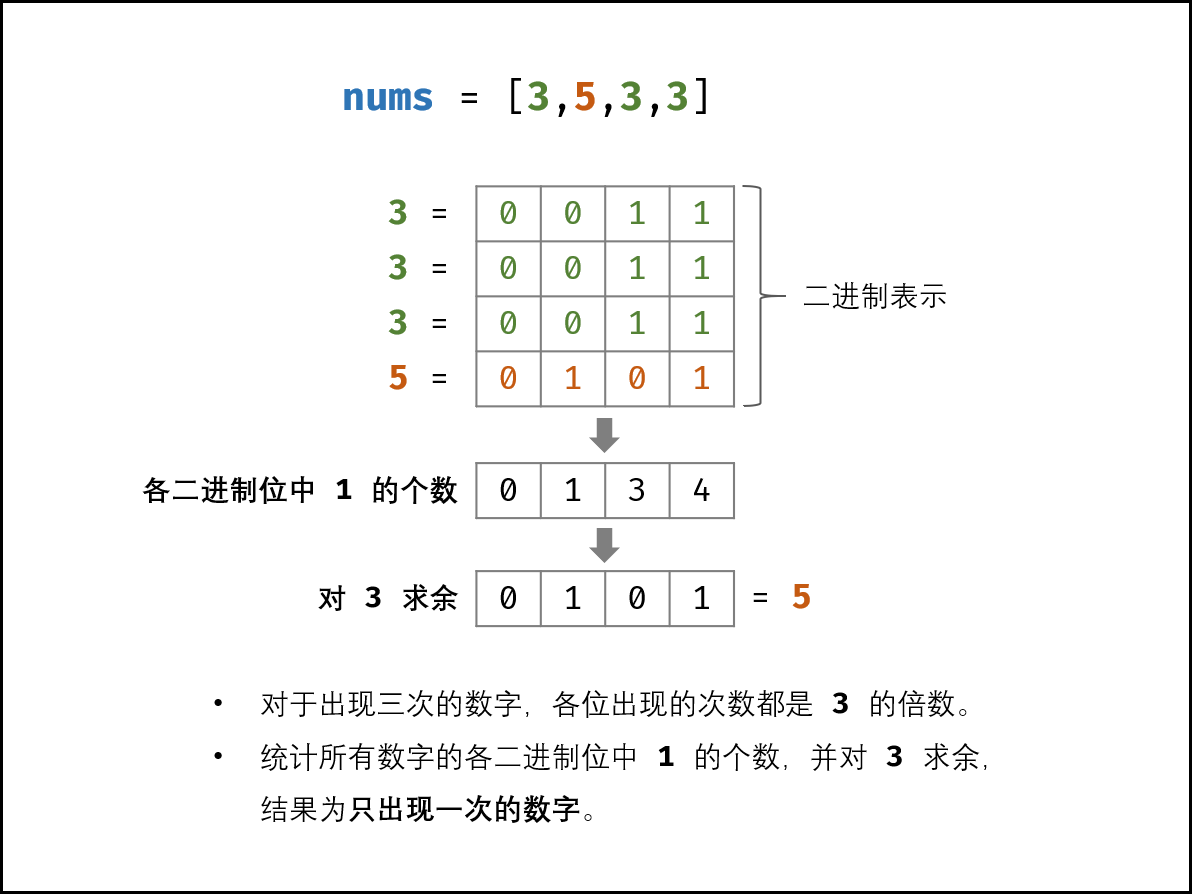
剑指 Offer II 004. 只出现一次的数字

给你一个整数数组 nums ，除某个元素仅出现一次外，其余每个元素都恰出现 三次。请你找出并返回那个只出现了一次的元素。

输入：nums = [2,2,3,2]
输出：3

方法1：显然这是使用位运算。我们可以统计每个数的每个位的情况。若每个数的第i位求和后，对3求余数为0，则目标数的第i位也为0，否则为1。那么这样目标数的二进制位情况便可以统计出来。

public int singleNumber(int[] nums) {
    // int的32位，对应位累加求和对3求余数，余数不为0，则当前位是那个只出现一次的数的对应位
    int res = 0;
    for(int i=0;i<32;i++){
        int total = 0;
        for(int num:nums){
            total+=(num>>i)&1;
        }
        if(total%3!=0){
            res |= (1<<i);
        }
    }
    return res;
}

剑指 Offer II 005. 单词长度的最大乘积

给定一个字符串数组 words，请计算当两个字符串 words[i] 和 words[j] 不包含相同字符时，它们长度的乘积的最大值。假设字符串中只包含英语的小写字母。如果没有不包含相同字符的一对字符串，返回 0。

示例1：

输入: words = ["abcw","baz","foo","bar","fxyz","abcdef"]
输出: 16
解释: 这两个单词为 "abcw", "fxyz"。它们不包含相同字符，且长度的乘积最大。

示例2：

输入: words = ["a","aa","aaa","aaaa"]
输出: 0
解释: 不存在这样的两个单词

思路：将判断两个字符串是否含有相同字符的判断的时间复杂度降为\(O(1)\)，是关键。可以采用位运算。时间复杂度：\(O(L+n^2)\)，L指全部单词的长度之和，n指单词数组的长度。

public int maxProduct(String[] words) {
    // 关键是将判断两个字符串是否含有相同的字符的时间复杂度降到O(1)
    // 可以使用位操作，将一个字符串的字母映射到26个位上，则该二进制所对应的数字可以代表该字符串
    // 采用&操作，可以判断两个字符串是否含有相同的字符
    int[] mask = new int[words.length];
    // 初始化mask数组
    for (int i = 0; i < words.length; i++) {
        for (int j = 0; j < words[i].length(); j++) {
            mask[i] |= 1<<(words[i].charAt(j)-'a');
        }
    }
    int res = 0;
    for (int i = 0; i < words.length-1; i++) {
        for (int j = i+1; j < words.length; j++) {
            // 若没有相同的字母，则更新max
            if((mask[i]&mask[j])==0){
                res = Math.max(res,words[i].length()* words[j].length());
            }
        }
    }
    return res;
}

当然该方法还可以进一步优化，存在两个串其未表示相同，eg：‘a’,’aaaa’，则可以使用一个hashMap来记录，对应mask值得最大字符串长度，然后，更新两串长度乘积最大值得时候，只需变量hashMap的key即可。

public int maxProduct(String[] words) {
    // 关键是将判断两个字符串是否含有相同的字符的时间复杂度降到O(1)
    // 可以使用位操作，将一个字符串的字母映射到26个位上，则该二进制所对应的数字可以代表该字符串
    // 采用&操作，可以判断两个字符串是否含有相同的字符
    HashMap<Integer, Integer> map = new HashMap<>();
    // 初始化mask数组
    for (int i = 0; i < words.length; i++) {
        int mask = 0;
        for (int j = 0; j < words[i].length(); j++) {
            mask |= 1<<(words[i].charAt(j)-'a');
        }
        if(words[i].length()>map.getOrDefault(mask,0)){
            map.put(mask,words[i].length());
        }

    }
    int res = 0;
    Set<Integer> keySet = map.keySet();
    for(Integer mask1:keySet){
        for(Integer mask2:keySet){
            if((mask1&mask2)==0){
                res = Math.max(res,map.get(mask1)*map.get(mask2));
            }
        }
    }
    return res;
}

剑指 Offer II 007. 数组中和为 0 的三个数

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a ，b ，c ，使得 a + b + c = 0 ？请找出所有和为 0 且不重复的三元组。

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

该题目的关键是降低时间复杂度，可以先枚举一个数，寻找另外两个数的和为第一个数的相反数。外层循环枚举第一个数，内层循环采用双指针将问题转换为两数之和的问题。题目要求不重复。则需要先排序，排序的时间复杂度为\(O(logn)\) 。之后可以利用排序后的特点，进行重复情况的排除。

public List<List<Integer>> threeSum(int[] nums) {
    Arrays.sort(nums);
    List<List<Integer>> res = new ArrayList<>();
    for (int i = 0; i < nums.length; i++) {
        // 结果需要不重复，所以此处需要排除重复
        if(i>0 && nums[i]==nums[i-1]){
            continue;
        }
        int target = -nums[i];
        int third = nums.length-1;
        for (int second = i+1; second < nums.length; second++) {
            // 此处排序第二个数的重复情况
            if(second>i+1 && nums[second]==nums[second-1]){
                continue;
            }
            // 寻找第三个数
            while (second<third && nums[second]+nums[third]>target){
                third--;
            }
            if (third==second){
                break;
            }
            // 更新res
            if((nums[second]+nums[third])==target){
                List<Integer> cur = new ArrayList<>();
                cur.add(nums[i]);
                cur.add(nums[second]);
                cur.add(nums[third]);
                res.add(cur);
            }
        }

    }
    return res;
}

posted @ 2022-05-05 13:26 星星点灯er 阅读(93) 评论(0) 收藏举报

刷新页面返回顶部