[本文链接:http://www.cnblogs.com/breezedeus/p/3496819.html,转载请注明出处]
从等式约束的最小化问题说起:
![]()
上面问题的拉格朗日表达式为:
![]()
也就是前面的最小化问题可以写为:
\(
\min\limits_{x} \max\limits_{y} L(x, y)
\) 。
它对应的对偶问题为:
\(
\max\limits_{y} \min\limits_{x} L(x, y)
\) 。
下面是用来求解此对偶问题的对偶上升迭代方法:
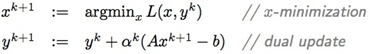
这个方法在满足一些比较强的假设下可以证明收敛。
为了弱化对偶上升方法的强假设性,一些研究者在上世纪60年代提出使用扩展拉格朗日表达式(augmented Lagrangian)代替原来的拉格朗日表达式:
![]()
其中\(\rho > 0\)。对应上面的对偶上升方法,得到下面的乘子法(method of multipliers):
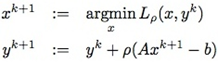
注意,乘子法里把第二个式子里的\(\alpha^k\)改成了扩展拉格朗日表达式中引入的\(\rho\)。这不是一个随意行为,而是有理论依据的。利用\(L(x, y)\)可以导出上面最小化问题对应的原始和对偶可行性条件分别为(\( \frac{\partial L} {\partial y} = 0\),\( \frac{\partial L} {\partial x} = 0\)):
![]()
既然\(x^{k+1}\) 最小化 \( L_{\rho}(x, y^{k})\),有:
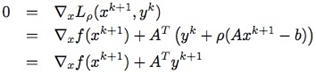
上面最后一个等式就是利用了\( y^{k+1} = y^{k} + \rho(A x^{k+1}-b) \)。从上面可知,这种\(y^{k+1}\)的取法使得\( (x^{k+1}, y^{k+1}) \)满足对偶可行条件\( \frac{\partial L} {\partial x} = 0 \)。而原始可行条件在迭代过程中逐渐成立。
乘子法弱化了对偶上升法的收敛条件,但由于在x-minimization步引入了二次项而导致无法把x分开进行求解(详见[1])。而接下来要讲的Alternating Direction Method of Multipliers (ADMM)就是期望结合乘子法的弱条件的收敛性以及对偶上升法的可分解求解性。ADMM求解以下形式的最小化问题:
![]()
其对应的扩展拉格朗日表达式为:
![]()
ADMM包括以下迭代步骤:
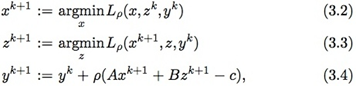
ADMM其实和乘子法很像,只是乘子法里把\(x\)和\(z\)放一块求解,而ADMM是分开求解,类似迭代一步的Gauss-Seidel方法。其中(3.4)中的推导类似于乘子法,只是使用了\(z^{k+1}\)最小化\( L_{\rho}(x^{k+1}, z, y^k) \):
![]()
其中用到了\(z\)对应的对偶可行性式子:
\(
\frac{\partial L} {\partial z} = \nabla g(z) + B^Ty = 0
\)
定义新变量\( u=\frac{1}{\rho}y \),那么(3.2-3.4)中的迭代可以变为以下形式:
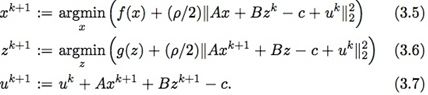
在真正求解时通常会使用所谓的over-relaxation方法,也即在\(z\)和\(u\)中使用下面的表达式代替其中的\( Ax^{k+1} \):
\(
\alpha^k A x^{k+1} - (1-\alpha^k)(B z^k - c)
\),
其中\(\alpha^k\)为relaxation因子。有实验表明\(\alpha^k \in [1.5, 1.8]\)可以改进收敛性([2])。
下面让我们看看ADMM怎么被用来求解大型的机器学习模型。所谓的大型,要不就是样本数太多,或者样本的维数太高。下面我们只考虑第一种情况,关于第二种情况感兴趣的读者可以参见最后的参考文献[1, 2]。样本数太多无法一次全部导入内存,常见的处理方式是使用分布式系统,把样本分块,使得每块样本能导入到一台机器的内存中。当然,我们要的是一个最终模型,它的训练过程利用了所有的样本数据。常见的机器学习模型如下:
\(
\text{minimize }_{x} \sum_{j=1}^{J} f_j(x) + g(x)
\),
其中\(x\)为模型参数,\(f_j(x)\)对应第\(j\)个样本的损失函数,而\(g(x)\)为惩罚系数,如\(g(x) = ||x||_1\)。
假设把\(J\)个样本分成\(N\)份,每份可以导入内存。此时我们把上面的问题重写为下面的形式:
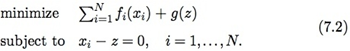
除了把目标函数分成\(N\)块,还额外加了\(N\)个等式约束,使得利用每块样本计算出来的模型参数\(x_i\)都相等。那么,ADMM中的求解步骤(3.2)-(3.4)变为:
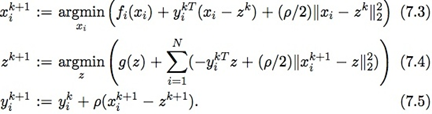
例如求解L1惩罚的LR模型,其迭代步骤如下(\( u=\frac{1}{\rho}y \),\(g(z)=\lambda ||z||_1\)):
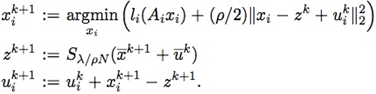
其中\(\bar{x} \doteq \frac1N \sum_{i}^N x_i\),\(\bar{y}\)的定义类似。
在分布式情况下,为了计算方便通常会把\(u\)的更新步骤挪在最前面,这样\(u\)和\(x\)的更新可以放在一块:
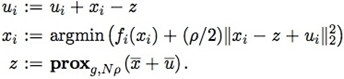
ADMM的框架确实很牛逼,把一个大问题分成可分布式同时求解的多个小问题。理论上,ADMM的框架可以解决大部分实际中的大尺度问题。我自己全部实现了一遍这个框架,主要用于求解LR问题,下面说说我碰到的一些问题:
1. 收敛不够快,往往需要迭代几十步。整体速度主要依赖于\(x_i\)更新时所使用的优化方法,个人建议使用liblinear里算法,但是不能直接拿来就用,需要做一些调整。
2. 停止准则和\(\rho\)的选取:停止准则主要考量的是\(x_i\)和\(z\)之间的差异和它们本身的变动情况,但这些值又受\(\rho\)的取值的影响。它们之间如何权衡并无定法。个人建议使用模型在测试集上的效果来确定是否停止迭代。
3. 不适合MapReduce框架实现:需要保证对数据的分割自始至终都一致;用MPI实现的话相对于其他算法又未必有什么优势(如L-BFGS、OwLQN等)。
4. relaxation步骤要谨慎:\(\alpha\)的取值依赖于具体的问题,很多时候的确可以加快收敛速度,但对有些问题甚至可能带来不收敛的后果。用的时候不论是用x -> z -> u的更新步骤,还是用u -> x -> z的更新步骤,在u步使用的x_hat要和在z步使用的相同(使用旧的z),而不是使用z步刚更新的z重算。
5. warm start 和子问题求解逐渐精确的策略可以降低\(x_i\)更新时的耗时,但也使得算法更加复杂,需要设定的参数也增加了。
[References]
[1] S. Boyd. Alternating Direction Method of Multipliers (Slides).
[2] S. Boyd et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers, 2010.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号