树状数组

acwing - 楼兰图腾

树状数组操作

 

(1)add(x, k)函数表示将序列中第x个数加上k, 同时范围覆盖到x的数也要加上k

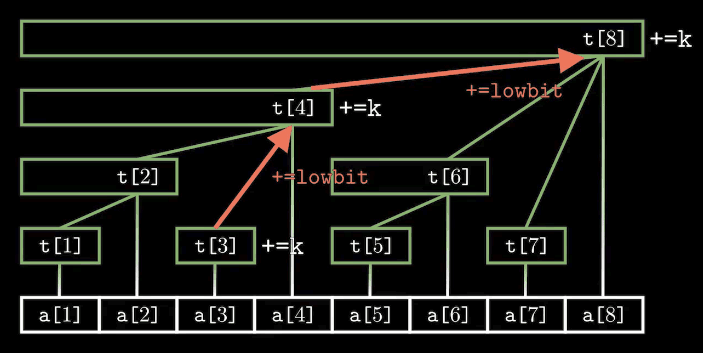
实现：

void add(int x, int k)
{
    for(int i = x; i <= n; i += lowbit(i))
        tr[i] += k;
}

(2)sum(x)函数为查询操作，查询前x个数的和，每次将下标-lowbit(i)之后，所有t[i]的和

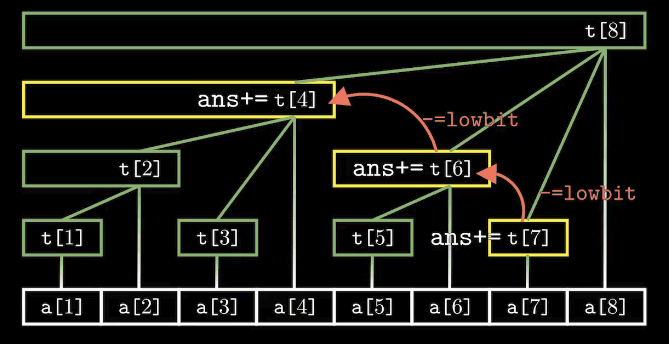
实现：

int sum(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

楼兰图腾

#include <iostream>
#include <cstring>
using namespace std;

const int N = 200010;

typedef long long LL;

int n;
int Greater[N], Lower[N];      
//Greater[i]表示在第i个位置左边，比a[i]大的数的个数
//Lower[i]表示在第i个位置左边，比a[i]小的数的个数

int tr[N];     //tr[i]表示树状数组i覆盖范围内的数的个数和
int a[N];


//返回x的最后一位1
int lowbit(int x)
{
    return x & (-x);
}

/*将x以及所有受x影响的tr[i](即覆盖范围包含x的tr[i])都+c

举个例子感受一下原因：
若add(3,1),即向序列中加入一个数字3，此时tr[3] += 1, tr[4] += 1
sum(5)表示此时树状数组中<=5的数字的个数和，而sum(5) = tr[1] + tr[4]
因此向序列中加入一个3，通过影响tr[4]的值，从而使sum(5) += 1,统计到刚刚加入序列中的3
*/
void add(int x, int c)
{
    for(int i = x; i <= n; i += lowbit(i))
        tr[i] += c;
}

//求所有已经加入树状数组中的<=x的数字的个数和
int sum(int x)
{
    int res = 0;
    for(int i = x; i; i -= lowbit(i))
        res += tr[i];
    return res;
}

int main()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i ++)
        scanf("%d", &a[i]);

    //从左往右开始统计，求出在第i个位置左边，小于或大于a[i]的数的个数
    for(int i = 1; i <= n; i ++)
    {
        int j = a[i];
        Greater[i] = sum(n) - sum(j);  //采用前缀和的思想，用小于等于n的数的个数—小于等于a[i]的数的个数
        Lower[i] = sum(j - 1);
        add(j, 1);
    }

    memset(tr, 0, sizeof tr);    //重置tr数组

    //从右往左开始统计，求出在第i个位置右边，小于或大于a[i]的数的个数
    LL res1 = 0, res2 = 0;
    for(int i = n; i; i --)
    {
        int j = a[i];
        res1 += (LL)Greater[i] * (sum(n) - sum(j));    //乘法原理
        res2 += (LL)Lower[i] * sum(j - 1);
        add(j, 1);
    }
    printf("%lld %lld", res1, res2);
    return 0;
}