焦虑的蚂蚁

一条长度为n的小径上，挤满了m只蚂蚁，每只蚂蚁有一个初始前进方向（向左或是向右），蚂蚁们的前进速度相同且均为1。小径的两端，均放着上了锁的箱子，箱内盛有美味的食物，蚂蚁们争相前进离开小径。不幸的是，小径十分狭窄，当两只蚂蚁相遇时，它们不得不掉头向着相反的方向前进。当所有的蚂蚁都离开小径时，锁才能够打开，蚂蚁们才能获得美味的食物。因此，蚂蚁们十分焦虑，它们想知道，到底花费多少的时间，它们才能够吃到美味的食物。你能够帮助他们解决问题吗？

输入描述:

第一行，2个整数n，m（1≤m<n≤100000，n,m均为整数），分别代表小径的长度，蚂蚁的数量。
接下来m行，每行2个数，分别代表蚂蚁的初始方向（0代表向左，1代表向右），蚂蚁的初始坐标x满足x为整数且0<x<n，蚂蚁走到坐标0或坐标n即代表离开小径。
数据保证每个坐标上最多有1只蚂蚁。数据保证给出的蚂蚁初始坐标为从小到大。

输出描述:

一行，对结果四舍五入，输出1个整数，代表蚂蚁吃到美味的食物的时间。

分析

假设只有一只蚂蚁，那么对于向左的蚂蚁，离开的时间为\(x\)。向右的蚂蚁，时间为\(n-x\)。

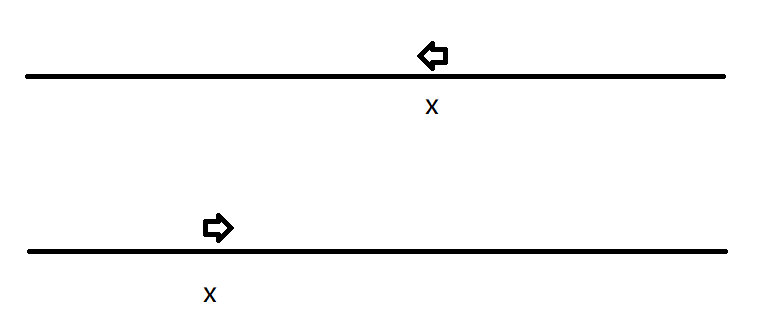
现在有两只蚂蚁，它们的位置有下列情况：

二者是同向的，那么时间为\(max(x1,x2)\)或\(max(n-x1,n-x2)\)（都向右）

背对背，时间为\(max(x1,n-x2)\)

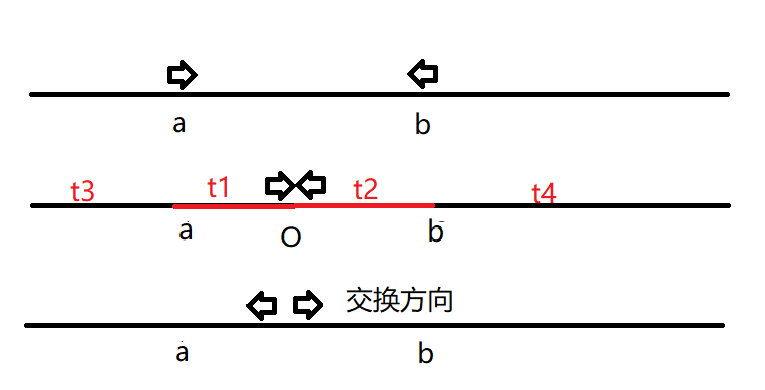
重点分析面对面的情况，假设蚂蚁a走到相遇点使用了\(t_1\)， 蚂蚁b使用了\(t_2\)，此时它们交换方向，蚂蚁a一共走了\(2*t_1+t_3\)到达出口，蚂蚁b走\(2*t_2+t_4\)到达出口。我们可以想象一下，如果它们不交换方向而是穿透继续走的话，蚂蚁a走了\(t_1+t_2+t_4\)到达出口，蚂蚁b走\(t_1+t_2+t_3\)到达出口，无论是否交换方向，它们总花费的时间是一样的，而且\(t_1=t_2\)，因此，每只蚂蚁的时间不受交换方向的影响，是独立的。
通过上述分析，只需算出每只蚂蚁的时间更新最大值即可。

AC

#include <iostream>
using namespace std;
int main()
{
    int n,m;cin>>n>>m;
    int maxx=0;
    while(m--)
    {
        int a,b;cin>>a>>b;
        if(a) maxx=max(maxx,n-b);
        else maxx=max(maxx,b);
    }
    cout<<maxx;
    return 0;
}

链接：https://ac.nowcoder.com/acm/problem/21201
来源：牛客网