支持向量机（SVM）

SVM支持向量机

简述：

给定一个特征空间上的数据集：
$T = $ { \((x_{1}, y_{1}), (x_{2}, y_{2}), ...(x_{N}, y_{N})\) }
其中，\(x_{i} \in \mathrm{R}^n, y_{i} \in\) {\(\mathrm{+1, -1}\) }
假设数据集线性可分，即存在一个分割超平面 \(w^* \cdot x + b^*\), 使得 \(y_{i} = \mathrm{sign}(w^* \cdot x_{i} + b^*), {\forall} i \in [1, n]\)
那么，就可以用分类决策函数 \(f(x) = \mathrm{sign}(w^* \cdot x + b^*)\) 对不在训练样本中的 \(x \in \mathrm{R}^n\) 进行类别的预测。

化简问题

\(\qquad \qquad \max_{w, b} \frac{\widehat{\gamma}}{||w||}\)
\(\qquad \qquad \frac{\widehat{\gamma}}{||w||} = \min_{i = 1}^{N} \frac{y_{i}}{||w||}(w \cdot x_{i} + b)\)

\(\Rightarrow \qquad \max_{w, b} \frac{\widehat{\gamma}}{||w||}\)
\(\qquad \quad \mathrm{s.t.} \qquad y_{i}(w \cdot x_{i} + b) \ge \widehat{\gamma}\)

这个 \(\widehat{\gamma}\) 是给定 \(w,b\) 情况下的最小函数间隔，即 \(\min_{w,b} \quad y_{i}(w \cdot x_{i} + b)\)
在确定 \((w, b)\) 时，显然可知 \((\alpha w, \alpha b)\) 表示的和原 \((w,b)\) 是同一个解。
设 \(\widehat{\gamma}\) 是 \((w,b)\) 下的最小函数间隔，求出对应的最小几何间隔是 \(\frac{\widehat{\gamma}}{||w||}\)，那么显然同时将 \(w,b\) 乘以一个倍数可以改变 \(\widehat{\gamma}\) 但肯定不会改变 \(\frac{\widehat{\gamma}}{||w||}\)。
那么，为了简化问题，我们不妨让 \(\widehat{\gamma}\) 等于 1.
原问题即可化为易于学习的问题：

\(\qquad \qquad \max_{w, b} \frac{1}{||w||}\)
\(\qquad \qquad y_{i}(w \cdot x_{i} + b) \ge 1\)

\(\Rightarrow\)
\(\qquad \qquad \max_{w, b} \frac{1}{||w||}\)
\(\qquad \qquad y_{i}(w \cdot x_{i} + b) -1 \ge 0\)

\(\Rightarrow\)
\(\qquad \qquad \min_{w, b} \frac{1}{2}||w||^2\)
\(\qquad \qquad y_{i}(w \cdot x_{i} + b) -1 \ge 0, i = 1, 2, 3....N\)

这是一个很标准的有约束优化问题。

前置知识

拉格朗日对偶性

原始问题

原始问题： $\min_{x \in R^n} f(x) $
\(\mathrm{s.t}\):
\(c_{i}(x) \leqslant 0, i = 1, 2,...k\)
\(h_{j}(x) = 0, j = 1,2...l\)

引进拉格朗日函数： \(L(x,\alpha, \beta)=f(x)+\sum_{i = 1}^{k} \alpha_{i}c_{i}(x)+\sum_{j=1}^{l} \beta_{j}h_{j}(x)\)
考虑原始问题：\(\theta_{P}(x)=\max_{\alpha, \beta: \alpha_{i} \ge 0} L(x,\alpha, \beta)\)
\(\theta_{P}(x) = \begin{cases} & \text{ } +\infty, \qquad 不满足约束 \\ & \text{ } f(x), \qquad 满足约束 \end{cases}\)
显然，若 \(x\) 不符合约束，则 \(\theta_{P}(x)=+\infty\), 否则 \(\theta_{P}(x)\) 的值会等于 \(f(x)\).
令 \(p^* = \min_{x} \theta_{P}(x) = \min_{x} \max_{\alpha, \beta: \alpha_{i} \ge 0}L(x, \alpha, \beta)\), 则 \(p^*\) 为原始问题的最优值.

对偶问题

定义： \(\theta_{D}(\alpha, \beta) = \min_{x} L(x,\alpha, \beta)\)
则问题 \(\max_{\alpha, \beta: \alpha \ge 0} \theta_{D}(\alpha, \beta) = \max_{\alpha, \beta: \alpha \ge 0} \min_{x} L(x, \alpha, \beta)\) 称为广义拉格朗日函数的极大极小问题.
定义对偶问题的最优解为 \(d^*\)

原始问题与对偶问题的关系

\(d^* \leqslant p^*\)

证明：

对任意 \(\alpha, \beta\) 和 \(x\) 有：
\(\theta_{D}(\alpha, \beta) = \min_{x} L(x, \alpha, \beta) \leqslant L(x, \alpha, \beta) \leqslant \max_{\alpha, \beta}L(x, \alpha, \beta) = \theta_{P}(x)\)
这意味着对于任意 \(\alpha, \beta, x\), 对偶问题的解都要小于等于原问题的解，即：
\(d^* \leqslant p^*\)

定理 1：假设 \(f(x)\) 和 \(c_{i}(x)\) 是凸函数，\(h_{j}(x)\) 是仿射函数；并且假设不等式约束 \(c_{i}(x)\) 是严格可执行的（存在 \(x\)，满足 \(c_{i}(x)<0\), \(i=1,2....k\))，则存在 \(x^*, \alpha^*, \beta^*\) ，使 \(x^*\) 是原始问题的解，\(\alpha^*, \beta^*\) 是对偶问题的解，且 \(p^*=d^*=L(x^*, \alpha^*, \beta^*)\)

定理 2： 若满足定理 1 中的条件，则 \(x^*, \alpha^*, \beta^*\) 分别是原始和对偶问题的解的充分必要条件是 \(x^*, \alpha^*, \beta^*\) 满足如下的 \(KKT\) 条件：

\(\nabla_{x}L(x^*, \alpha^*, \beta^*)=0\)
\(\alpha_{i}^*c_{i}(x^*)=0,i=1,2....k\)
\(c_{i}(x^*) \leqslant 0, i=1,2....k\)
\(\alpha_{i}^* \ge 0, i=1,2....k\)
\(h_{j}(x^*)=0,j=1,2....l\)

解释：KKT 条件给出了在满足强对偶性情况下原始问题的解 \(x^*\) 和对偶问题的解 \(\alpha^*, \beta^*\) 的关系。 这就意味着 KKT 条件具有如下重要性质：

1. 强对偶性成立时，对于任意优化问题，\(\mathrm{KKT}\) 条件是最优解的必要条件，即主问题最优解和对偶问题最优解一定满足 \(\mathrm{KKT}\) 条件。
2. 对于凸优化问题，\(\mathrm{KKT}\) 条件是充分条件，即满足 \(\mathrm{KKT}\) 条件的解一定是最优解。
3. 对于强对偶性成立的凸优化问题，\(\mathrm{KKT}\) 条件是充要条件，即 \(x^*\) 是主问题的最优解当且仅当存在 \(\mathrm{\alpha^*, \beta^*}\) 满足 \(\mathrm{KKT}\) 条件。

这几点非常重要，这意味着对于任意一个原始问题的解 \(x^*\) 和对偶问题的解 \(\alpha^*, \beta^*\), 他们一定要满足 \(\mathrm{KKT}\) 条件：求出一个 \(\alpha^*, \beta^*\), 就可以推出相应的 \(x^*\)。

SVM 学习的对偶算法

\(\mathrm{SVM}\) 问题的原始表达式：

\(\min_{w,b} \frac{1}{2}||w||^2\)
\(s.t\)
\(c_{i}(w)=y_{i}(w\cdot x_{i}+b) - 1 \leqslant 0,i=1,2...N\)
显然 \(c_{i}(w)\) 是关于 \(w\) 的凸函数，那么根据非负加权和的保凸性，广义拉格朗日函数 \(L(w,b,\alpha)\) 也是凸函数。
根据拉格朗日对偶性，考虑求解该问题的极大极小问题：\(\max_{\alpha_{i} \ge 0} \min_{w,b} L(w,b,\alpha)\)

(1) 求 \(\min_{w,b} L(w,b,\alpha)\)

此时将 \(\alpha\) 看作是常数，又因为 \(L(w,b,\alpha)\) 是凸函数，故可以直接对 \(w,b\) 求偏导来得到 \(w,b\) 关于 \(\alpha\) 的表达式。

\(\nabla_{w} L(w,b,\alpha)=w-\sum_{i=1}^{N}\alpha_{i}y_{i}x_{i}=0\)
\(\nabla_{b} L(w,b,\alpha)=-\sum_{i=1}^{N} \alpha_{i}y_{i}=0\)

由此可得：

\(w=\sum_{i=1}^{N} \alpha_{i}y_{i}x_{i}\)
\(\sum_{i=1}^{N} \alpha_{i}y_{i}=0\)

将求偏导得到的式子带回广义拉格朗日函数，可得：
\(\max_{w,b} L(w,b,\alpha)=-\frac{1}{2}\sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j}y_{i}y_{j}(x_{i} \cdot x_{j})+\sum_{i=1}^{N} \alpha_{i}\)

(2) 求 \(\min_{w,b}L(w,b,\alpha)\) 对 \(\alpha\) 的极大：

\(\max_{\alpha} -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j}y_{i}y_{j}(x_{i} \cdot x_{j})+\sum_{i=1}^{N} \alpha_{i}\)
\(\mathrm{s.t.}\)
\(\sum_{i=1}^{N} \alpha_{i} y_{i}=0\)
\(\alpha_{i} \ge 0, i=1,2,....N\)

求对 \(\alpha\) 的极大可以看作是取负数后的极小：
\(\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - \sum_{i=1}^{N} \alpha_{i}\)
\(\mathrm{s.t}\)：
\(\sum_{i=1}^{N} \alpha_{i} y_{i}=0\)
\(\alpha_{i} \ge 0, i=1,2,....N\)

显然，由于数据保证一定有正类和负类且数据线性可分，原始问题一定满足前置知识中的定理1，故对偶问题的解等于原始问题的解。

显然，\(\alpha^* = (\alpha_{1}^*, \alpha_{2}^*,......\alpha_{N}^*)^T\) 可求，而原问题的解也一定存在。

根据 \(\mathrm{KKT}\) 条件，因原问题和对偶问题的解 \(\alpha^*, w^*, b^*\) 都存在，故他们应该满足以下关系：

\((1)\) \(\nabla_{w} L(w^*, b^*, \alpha^*)=w^* - \sum_{i=1}^{N} \alpha_{i}^*y_{i}x_{i}=0\)
\((2)\) \(\nabla_{b} L(w^*, b^*, \alpha^*)=-\sum_{i=1}^{N} \alpha_{i}^*y_{i}=0\)
\((3)\) \(\alpha_{i}^*(y_{i}(w \cdot x_{i}+b))=0, i=1,2...N\)
\((4)\) \(c_{i}(w) = 1 - y_{i}(w^* \cdot x_{i}+b) \leqslant 0,i=1,2...N\)
\((5)\) \(\alpha_{i}^* \ge 0, i=1,2...N\)

显然，因为 \(w^*\) 不能全 \(0\)，故存在 \(a_{j}^*>0\)，由 \(\mathrm{KKT}\) 条件可知：\(y_{j}(w \cdot x_{j}+b)-1=0\)。
那么:

\(b^*=\frac{1}{y_{j}} -w^*x_{j}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^*y_{i}(x_{i} \cdot x_{j})\)
\(w^* = \sum_{i=1}^{N} \alpha_{i}^*y_{i}x_{i}\)

总结：

先将原问题转换成极大极小的对偶问题并求出 \(\alpha^*\).
根据 \(\alpha^*\), 可计算出：

\(w^* = \sum_{i=1}^{N} \alpha_{i}^*y_{i}x_{i}\)
\(b^*=y_{j}-\sum_{i=1}^{N} \alpha_{i}^*y_{i}(x_{i} \cdot x_{j})\)

分类决策函数可以写成：\(f(x)=\mathrm{sign}(w^* \cdot x + b^*)\)

核技巧

当数据严格线性可分时，可以使用 \(\mathrm{SVM}\) 进行求解。
当数据不能直接线性分类时，就要构造映射，将输入从 \(\mathrm{R}^n\) 空间映射到特征空间；在特征空间中就可以使用 \(\mathrm{SVM}\) 了。

核函数

设 $\chi $ 为输入空间（例如常见的 \(\mathrm{R}^n\) 空间），\(H\) 为特征空间，如果存在一个从 \(\chi\) 到 \(H\) 的映射：

\(\phi(x): \chi \rightarrow H\)

使得对于所有的 \(x,z \in \chi\), 函数 \(K(x,z)\) 满足条件：

\(K(x,z) = \phi(x) \cdot \phi(z)\)

则称 \(K(x,z)\) 为核函数，\(\phi(x)\) 为映射函数，式子中 \(\phi(x) \cdot \phi(z)\) 为 \(H\) 特征空间中的内积。

最直观的想法是，在输入样本时就对每个样本进行 \(x \rightarrow \phi(x)\) 的映射操作。

根据推导，发现最后的式子中 \(x_{i}\) 的操作仅仅有 \(x_{i} \cdot x_{j}\)，那么就可以定义 \(K(x,z)=\phi(x) \cdot \phi(z)\)。

这样做的好处就是不用显式定义出 \(x \rightarrow \phi(x)\)， 可以将 \(x\) 投射到一个维数很大很大的空间（甚至是无穷维）

例：设输入空间是 \(\mathrm{R}^2\), 核函数是 \(K(x,z) = (x \cdot z) ^2\)，那么有:

\(K(x,z)=(x^{(1)}z^{(1)})^2+2x^{(1)}z^{(1)}x^{(2)}z^{(2)}+(x^{(2)}z^{(2)})^2\)

而对于该核函数，一个合法的映射 \(\phi(x)\) 是：

\(\phi(x)=((x^{(1)})^2, \sqrt 2x^{(1)}x^{(2)}, (x^{(2)})^2)^T\)

这意味着，使用了核函数 \(K(x,z)\) 意味着在输入阶段就将 \(x\) 映射为 \(\phi(x)\).
显然，在更高维度会更有可能满足线性可分，而在实际操作中却没有显示地增加输入样本 \(x\) 的维度。

使用核技巧后，优化目标和表达式分别为：

\(W(\alpha)= \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j}y_{i}y_{j}K(x_{i}, x_{j})-\sum_{i=1}^{N} \alpha_{i}\)

\(f(x)=\mathrm{sign}(\sum_{i=1}^{N} \alpha_{i}^*y_{i}K(x_{i},x)+b^*)\)

常用核函数

构造出新的核函数比较困难，而且需要验证。
事实上，在实际问题中往往会应用已有的核函数，下面给出常用的核函数。

\(\mathrm{1.}\) 多项式核函数

\(K(x,z) = (x \cdot z + 1)^p\)

\(\mathrm{2.}\) 高斯核函数

\(K(x,z) = \exp(-\frac{||x-z||^2}{2 \sigma^2})\)

\(\mathrm{3.}\) 字符串核函数

序列最小最优化算法

\(\mathrm{SMO}\) 算法要解如下凸二次规划的对偶问题：

\(\min_{\alpha} \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j}y_{i}y_{j}K(x_{i}, x_{j}) - \sum_{i=1}^{N} \alpha_{i}\)

\(\mathrm{s.t.}\)
\(\sum_{i=1}^{N} \alpha_{i}y_{i}=0\)
\(0\leqslant \alpha_{i} \leqslant C\), \(i=1,2,...N\)

在推出 \(\alpha^*\) 之后，可以反推出 \(w^*, b^*\)：

\(w^* = \sum_{i=1}^{N} \alpha_{i}^*y_{i}x_{i}\)
\(b^*=y_{j}-\sum_{i=1}^{N} \alpha_{i}^*y_{i}K(x_{i} ,x_{j})\)

\(\mathrm{SMO}\) 算法的基本思路：

1. 如果所有变量的解（通过 \(\alpha\) 的解可以直接算出 \(x\) 的解）都满足此最优化问题的 \(\mathrm{KKT}\) 条件，那么这个最优化问题的解就得到了。
2. 如果所有变量的解不满足 \(\mathrm{KKT}\) 条件，那么选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题。
3. (2) 中的子问题有两个变量，一个是违反 \(\mathrm{KKT}\) 条件最严重的一个，另一个由约束条件自动确定。

\(\mathrm{SMO}\) 算法包括两个部分：求解两个变量二次规划的解析方法和选择变量的启发式方法。

\(\min_{\alpha_{1}, \alpha_{2}} W(\alpha_{1}, \alpha_{2}) = \frac{1}{2} K_{11}\alpha_{1}^2 + \frac{1}{2}K_{22}\alpha_{2}^2 + y_{1}y_{2} K_{12}\alpha_{1}\alpha_{2} - (\alpha_{1} + \alpha_{2}) + y_{1}\alpha_{1}\sum_{i=3}^{N} y_{i}\alpha_{i}K_{i1} + y_{2}\alpha_{2}\sum_{i=3}^{N} y_{i}\alpha_{i}K_{i2}\)
$\mathrm{s.t.} $
\(\qquad \qquad y_{1}\alpha_{1} + y_{2}\alpha_{2} = -\sum_{i = 3}^{N} y_{i} \alpha_{i}\)
\(\qquad \qquad 0\leqslant \alpha_{i} \leqslant C, \qquad i = 1, 2\)

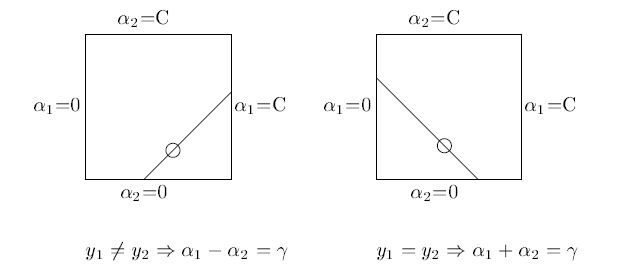
两个变量二次规划问题的求解

设 \(g(x) = \sum_{i=1}^{N} \alpha_{i} y_{i} K(x_{i}, x) + b\)

令：\(E_{i} = g(x_{i})-y_{i} = (\sum_{j=1}^{N} \alpha_{j}y_{j}K(x_{j}, x) + b) - y_{i}, \quad i = 1, 2\)
即 \(i = 1, 2\) 时，\(E_{i}\) 为函数 \(g(x)\) 对输入 \(x_{i}\) 的预测值与真实输出 \(y_{i}\) 之差。

定理：最优化问题沿着约束方向未经剪辑时的解是：

\(\qquad \qquad \alpha^{new}_{2} = \alpha^{old}_{2} + \frac{y_{2}(E_{1} - E_{2})}{\eta }\)

其中，
\(\qquad \qquad \eta = K_{11} + K_{22} - 2K_{12}\)

经过边界 \([L,H]\) 的剪辑后 \(\alpha_{2}\) 的解是：

\(\alpha_{2}^{new} = \begin{cases} & \text{ }H \qquad \alpha^{new}_{2} > H \\ & \text{ } \alpha^{new}_{2} \qquad L \leqslant \alpha^{new}_{2} \leqslant H \\ & \text{ } L \qquad \alpha_{2}^{new} < L \end{cases}\)

可由 \(\alpha_{2}^{new}\) 求得 \(\alpha_{1}^{new}\):
$\qquad \qquad \alpha_{1}^{new} = \alpha_{1}^{old} + y_{1}y_{2}(\alpha_{2}^{old} - \alpha_{2}^{new}) $

变量的选择方法

第一个变量：违反 \(\mathrm{KKT}\) 条件最严重的样本点。
第二个变量：依次遍历每一个 \(\alpha_{i}\)，与第一个点一起尝试进行更新。若更新幅度不大，则再换 \(\alpha_{2}\).

\(\mathrm{SMO}\) 算法流程：

（1）选初值 \(\alpha^{(0)} = 0, \qquad k = 0\)
（2）选取优化变量 \(\alpha_{1}^{(k)}, \alpha_{2}^{(k)}\)，按照上面的更新方式进行更新，得到 \(\alpha_{1}^{(k + 1)},\alpha_{2}^{(k + 1)}\).
（3）若在精度范围内满足约束条件，就停止；否则转到 （2）

最后求得 \(\alpha^*\)，可以推得 \(w^*, b^*\)，得到支持向量机：

\(\qquad \qquad f(x) = \mathrm{sign}(\sum_{i = 1}^{N} \alpha_{i} ^*y_{i}K(x_{i}, x_{j}) + b^*)\)