segment tree beats

1.线段树维护历史最值

例题：洛谷P4314 CPU监控

令 $(x,y)$ 标记表示将线段树当前区间所有数字变成 $\mathrm{max(a[i]+x, y)}$

通过 $(x,y)$ 标记可以实现区间赋值，区间加法，以及 $\mathrm{max(a[i]+x, y)}$

在处理线段树标记的时候，要考虑标记如何结合在一起.

对于标记 $(x,y)$ 与 $(x', y')$，按照顺序结合后的结果就是 $\mathrm{(x+x', max(y+x', y')}$.

两个标记的结合是 $O(1)$ 的，故这种方法可以采用 pushdown 的方式进行下传.

考虑如何处理历史最值.

令历史最值标记 $(x,y)$ 表示可以令常数 $a$ 最大化的 $(x,y)$ 标记.

父区间的标记被打上的时间显然晚于子区间标记被打上的时间，否则父区间的标记就被清空了.

假设子区间的当前最大值为 $\mathrm{nmax}$，当前标记为 $(x,y)$，父区间的历史最值标记为 $(x',y')$

新的最优历史最值标记显然可以是 $(x,y)$ 与 $(x',y')$ 的结合.

对于常数 $a$ 的 $(x,y)$ 操作我们只会用到 $x,y$ 其中一个，所以历史最值标记中 $x,y$ 分别越大越好.

故上文子区间的历史最值标记就是原来的历史最值标记与新结合成的最值标记取 $\mathrm{max}$ 的结果.

在下传标记的时候一定先下传历史最值标记，因为历史最值在下传时需要用到子节点的当前标记.

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm> 
#define N 100007 
#define ll long long 
#define ls now<<1 
#define rs now<<1|1
#define setIO(s) freopen(s".in","r",stdin) 
using namespace std; 
int n,Q;  
const int inf=(1<<30)-1;  
struct data {
    int x,y;  
    data(int a=0,int b=-inf) { x=a,y=b;}   
    data operator+(const data b) const {
        return data(max(-inf, x+b.x), max(y+b.x, b.y));  
    }
    data operator*(const data b) const {
        return data(max(x, b.x), max(y, b.y));  
    }
}ntag[N<<2],ptag[N<<2];  
int nmax[N<<2],pmax[N<<2];  
void pushup(int now) {
    nmax[now]=max(nmax[ls], nmax[rs]); 
    pmax[now]=max(pmax[ls], pmax[rs]);  
}
void build(int l,int r,int now) {
    ntag[now]=ptag[now]=data();  
    if(l==r) {
        scanf("%d",&nmax[now]); 
        pmax[now]=nmax[now];  
        return ;       
    }
    int mid=(l+r)>>1;  
    build(l, mid, ls); 
    build(mid+1, r, rs);  
    pushup(now);   
}
// 打当前标记.  
void markn(int now, data v) {
    ntag[now]=ntag[now]+v;      
    nmax[now]=max(nmax[now]+v.x, v.y);    
}     
void markp(int now, data v) {
    pmax[now]=max(pmax[now], max(nmax[now]+v.x, v.y));   
    ptag[now]=ptag[now]*(ntag[now]+v);   
}
void pushdown(int now) {
    markp(ls, ptag[now]); 
    markp(rs, ptag[now]); 
    markn(ls, ntag[now]); 
    markn(rs, ntag[now]); 
    ntag[now]=ptag[now]=data(); 
}
void update(int l,int r,int now,int L,int R,data v) {         
    if(l>=L&&r<=R) {    
        markp(now, v);   
        markn(now, v);  
        return ; 
    }
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid)  update(l, mid, ls, L, R, v); 
    if(R>mid)   update(mid+1, r, rs, L, R, v); 
    pushup(now);
}
int queryn(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) return nmax[now]; 
    pushdown(now); 
    int mid=(l+r)>>1; 
    if(L<=mid&&R>mid) return max(queryn(l,mid,ls,L,R),queryn(mid+1,r,rs,L,R));  
    else if(L<=mid) return queryn(l,mid,ls,L,R); 
    else return queryn(mid+1,r,rs,L,R); 
}
int queryp(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) return pmax[now]; 
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid&&R>mid) return max(queryp(l,mid,ls,L,R),queryp(mid+1,r,rs,L,R));  
    else if(L<=mid) return queryp(l,mid,ls,L,R); 
    else return queryp(mid+1,r,rs,L,R);  
}
int main() {
    // setIO("input");   
    scanf("%d",&n);  
    build(1, n, 1);  
    scanf("%d",&Q); 
    for(int i=1;i<=Q;++i) {    
        char op[2];  
        int l,r,z; 
        scanf("%s",op); 
        scanf("%d%d",&l,&r); 
        if(op[0]=='Q') printf("%d\n",queryn(1,n,1,l,r)); 
        if(op[0]=='A') printf("%d\n",queryp(1,n,1,l,r)); 
        if(op[0]=='P') scanf("%d",&z),update(1,n,1,l,r,data(z, -inf));  
        if(op[0]=='C') scanf("%d",&z),update(1,n,1,l,r,data(-inf, z));     
    }
    return 0; 
}

2.区间取 min/max

例题：HDU5306 Gorgeous Sequence

区间取 min 最基本的一道题.

对于线段树上每个区间，维护最大值，次大值，最大值出现次数.

在更新时，对于线段树的一个区间 $\mathrm{now}$，分 3 种情况讨论.

1. $\mathrm{mx[now]} \leqslant v$，直接返回.

2. $\mathrm{se[now]+1} \leqslant v \leqslant \mathrm{mx[now]-1}$，直接修改.

3. $v \leqslant \mathrm{se[now]}$，继续递归.

在分析复杂度时瓶颈在于第 3 种操作，经证明整体复杂度为 $O(n \log n)$.

证明：

对于线段树上的每个节点 $\mathrm{u}$，我们设 $\mathrm{p[u]}$ 代表 $u$ 的势能.

定义线段树每个节点的势能为所维护区间中不同数字种类.

初始情况，$\sum \mathrm{p[u]} \leqslant n \log n$.

每进行上述情况 3 的递归时，至少最大值和次大值会变成 $v$，故所访问到的点的势能会减小.

初始情况的势能为 $O( n \log n)$，遇到一次情况 3 势能至少减小 $1$，故情况 3 最多遇到 $O(n \log n)$ 次.

那么相比正常线段树多出来 $O(n \log n)$ 的复杂度，故总复杂度为 $O(n \log n)$.

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm> 
#define N  1000009 
#define ll long long 
#define ls now<<1 
#define rs now<<1|1
#define setIO(s) freopen(s".in","r",stdin) 
using namespace std;   
const int inf=(1<<30);  
ll sum[N<<2];         
int mx[N<<2],se[N<<2],cn[N<<2],len[N<<2];  
void pushup(int now) { 
    if(mx[ls]>mx[rs]){        
        mx[now]=mx[ls]; 
        cn[now]=cn[ls]; 
        se[now]=max(se[ls],mx[rs]);  
    }
    else if(mx[rs]>mx[ls]) {
        mx[now]=mx[rs]; 
        cn[now]=cn[rs]; 
        se[now]=max(se[rs],mx[ls]); 
    }
    else {
        mx[now]=mx[ls]; 
        cn[now]=cn[ls]+cn[rs]; 
        se[now]=max(se[ls],se[rs]);   
    }
    sum[now]=sum[ls]+sum[rs];  
}
void build(int l,int r,int now) {
    len[now]=r-l+1; 
    mx[now]=se[now]=-inf;  
    cn[now]=0,sum[now]=0;   
    if(l==r) {
        scanf("%d",&mx[now]);    
        cn[now]=1; 
        sum[now]=mx[now];   
        return ; 
    }   
    int mid=(l+r)>>1;
    build(l,mid,ls); 
    build(mid+1,r,rs); 
    pushup(now); 
}
// 与 v 取 min.  
void mark(int now, int v) {
    if(v<mx[now]) {
        sum[now]-=1ll*cn[now]*(mx[now]-v);    
        mx[now]=v;            
    } 
}
void pushdown(int now) {
    mark(ls, mx[now]); 
    mark(rs, mx[now]); 
}
void update(int l,int r,int now,int L,int R,int v) {
    if(v>=mx[now]) return ;   
    if(l>=L&&r<=R&&v>se[now]) {
        mark(now, v);  
        return ; 
    }
    pushdown(now); 
    int mid=(l+r)>>1; 
    if(L<=mid) update(l,mid,ls,L,R,v); 
    if(R>mid)  update(mid+1,r,rs,L,R,v); 
    pushup(now); 
}   
ll qsum(int l, int r, int now, int L, int R) {
    if(l>=L&&r<=R) return sum[now]; 
    pushdown(now);  
    ll re=0; 
    int mid=(l+r)>>1;  
    if(L<=mid)  re+=qsum(l,mid,ls,L,R); 
    if(R>mid)   re+=qsum(mid+1,r,rs,L,R); 
    return re; 
}
int qmax(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) return mx[now]; 
    pushdown(now); 
    int mid=(l+r)>>1; 
    if(L<=mid&&R>mid) return max(qmax(l,mid,ls,L,R),qmax(mid+1,r,rs,L,R));  
    else if(L<=mid) return qmax(l,mid,ls,L,R); 
    else return qmax(mid+1,r,rs,L,R);  
}   
void solve() {
    int n,m; 
    scanf("%d%d",&n,&m); 
    build(1,n,1);      
    for(int i=1;i<=m;++i) {
        int op,l,r,z; 
        scanf("%d%d%d",&op,&l,&r);  
        if(op==0) scanf("%d",&z),update(1,n,1,l,r,z);  
        if(op==1) printf("%d\n",qmax(1,n,1,l,r)); 
        if(op==2) printf("%lld\n",qsum(1,n,1,l,r));  
    }
}
int main() { 
    // setIO("input");  
    int T; 
    scanf("%d",&T); 
    while(T--) solve(); 
    return 0; 
}

例题：bzoj4695 最假女选手

在取 $\mathrm{min/max}$ 的基础上多了一个区间加.

在下传标记的时候先下传加法标记，后下传 $\mathrm{min/max}$ 标记.

整体时间复杂度是 $O(n \log^2 n)$ 的.

这里给一下证明：

假设只有加法和区间取 $\mathrm{min}$.

如果线段树上一个点左右儿子的最大值不同，就将这个点设为标记点.

在初始时刻，标记点为 $O(n)$ 个.

考虑区间取 $\mathrm{min}$ 操作会访问哪些节点：

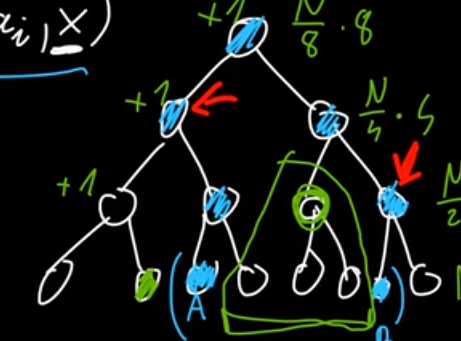
（摘自 errichto 大佬的视频截图）

假设线段树上的蓝点是我们正常要更新的区间.

在正常的线段树上，我们只会遍历蓝点，有 $O(\log n) $ 个.

因为我们要进行区间取 $\mathrm{min}$, 所以会遍历到一些绿点.

假设从一个蓝点进入绿点, 且每次只遍历绿点的一个子树, 那么复杂度是 $O(\log n)$ 的.

最坏情况是所遍历到的点中，只有最后一个点从被标记变为不被标记.

这等于说用了 $O(\log n)$ 次操作修改一个标记点.

如果在遍历一个绿点时会遍历绿点的左右儿子,则该绿点一定变为非标记点.

这就意味着多遍历一个儿子多一个 $O(\log n)$ 的复杂度，但是多消除了一个标记点.

所以，我们可以知道，消除一个标记点最多需要 $O(\log n)$ 的复杂度.

再考虑区间加法，显然只有蓝点可能变为标记点.

1.最开始的标记点有 $\mathrm{O(n)}$ 个.

2.加法操作最多增加 $O(Q \log n)$ 个标记点.

故消除标记点最多需要 $O((n+Q\log n) \log n)$, 整体复杂度为 $O(n \log^2 n)$.

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>   
#define N  500009 
#define ll long long 
#define ls now<<1 
#define rs now<<1|1   
#define setIO(s) freopen(s".in","r",stdin) 
using namespace std;   
const int inf=300000000; 
ll sum[N<<2];
int mx[N<<2],se[N<<2],mn[N<<2],m2[N<<2],c1[N<<2],c2[N<<2],len[N<<2],add[N<<2];  
void pushup(int now) {
    if(mx[ls]>mx[rs]) 
        mx[now]=mx[ls],se[now]=max(se[ls],mx[rs]),c1[now]=c1[ls];  
    else if(mx[rs]>mx[ls])  
        mx[now]=mx[rs],se[now]=max(mx[ls],se[rs]),c1[now]=c1[rs];  
    else mx[now]=mx[ls],se[now]=max(se[ls],se[rs]),c1[now]=c1[ls]+c1[rs];  
    if(mn[ls]<mn[rs])  
        mn[now]=mn[ls],m2[now]=min(m2[ls],mn[rs]),c2[now]=c2[ls];  
    else if(mn[rs]<mn[ls]) 
        mn[now]=mn[rs],m2[now]=min(m2[rs],mn[ls]),c2[now]=c2[rs];  
    else mn[now]=mn[ls],m2[now]=min(m2[ls],m2[rs]),c2[now]=c2[ls]+c2[rs];  
    sum[now]=sum[ls]+sum[rs];  
}
void mark_add(int now,int v) { 
    sum[now]+=1ll*len[now]*v;  
    mx[now]+=v,se[now]+=v;   
    mn[now]+=v,m2[now]+=v,add[now]+=v;  
}
// 最小值.       
void mark_min(int now,int v) {
    if(v>mn[now]) {
        sum[now]+=1ll*c2[now]*(v-mn[now]);   
        if(mx[now]==mn[now]) mx[now]=v;  
        if(se[now]==mn[now]) se[now]=v;  
        mn[now]=v;   
    }
}
// 最大值.  
void mark_max(int now,int v) {
    if(v<mx[now]) {
        sum[now]-=1ll*c1[now]*(mx[now]-v);   
        if(mn[now]==mx[now]) mn[now]=v;  
        if(m2[now]==mx[now]) m2[now]=v;  
        mx[now]=v;  
    }
}
void build(int l,int r,int now) {
    se[now]=-inf; 
    m2[now]=inf;  
    len[now]=r-l+1;  
    if(l==r) {
        scanf("%d",&mx[now]); 
        mn[now]=sum[now]=mx[now];   
        c1[now]=c2[now]=1;  
        return ;    
    }
    int mid=(l+r)>>1; 
    build(l,mid,ls); 
    build(mid+1,r,rs); 
    pushup(now); 
}  
void pushdown(int now) {
    if(add[now]) {
        mark_add(ls, add[now]); 
        mark_add(rs, add[now]);  
        add[now]=0;
    }
    mark_min(ls, mn[now]),mark_min(rs, mn[now]); 
    mark_max(ls, mx[now]),mark_max(rs, mx[now]);  
}
void ADD(int l,int r,int now,int L,int R,int v) {
    if(l>=L&&r<=R) {
        mark_add(now, v); 
        return ;  
    } 
    pushdown(now);
    int mid=(l+r)>>1;  
    if(L<=mid)  ADD(l,mid,ls,L,R,v); 
    if(R>mid)   ADD(mid+1,r,rs,L,R,v);  
    pushup(now);    
}
// 区间取 min
void upmin(int l,int r,int now,int L,int R,int v) {
    if(v>=mx[now]) return ;  
    if(l>=L&&r<=R&&v>se[now]) {
        mark_max(now, v);  
        return ;  
    }   
    pushdown(now);  
    int mid=(l+r)>>1; 
    if(L<=mid)  upmin(l,mid,ls,L,R,v); 
    if(R>mid)   upmin(mid+1,r,rs,L,R,v); 
    pushup(now);  
}  
void upmax(int l,int r,int now,int L,int R,int v) {
    if(v<=mn[now]) return ;  
    if(l>=L&&r<=R&&v<m2[now]) {
        mark_min(now, v); 
        return ;  
    }   
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid)  upmax(l,mid,ls,L,R,v); 
    if(R>mid)   upmax(mid+1,r,rs,L,R,v);  
    pushup(now);   
}
ll qsum(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) return sum[now];  
    pushdown(now); 
    int mid=(l+r)>>1;  
    ll re=0; 
    if(L<=mid)  re+=qsum(l,mid,ls,L,R); 
    if(R>mid)   re+=qsum(mid+1,r,rs,L,R); 
    return re; 
} 
int qmax(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) return mx[now]; 
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid&&R>mid) return max(qmax(l,mid,ls,L,R), qmax(mid+1,r,rs,L,R));  
    else if(L<=mid) return qmax(l,mid,ls,L,R); 
    else return qmax(mid+1,r,rs,L,R);  
}
int qmin(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) return mn[now];  
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid&&R>mid) return min(qmin(l,mid,ls,L,R), qmin(mid+1,r,rs,L,R)); 
    else if(L<=mid) return qmin(l,mid,ls,L,R);  
    else return qmin(mid+1,r,rs,L,R);  
}
int main() {
    // setIO("input");
    int n,m; 
    scanf("%d",&n); 
    build(1,n,1);  
    scanf("%d",&m); 
    for(int i=1;i<=m;++i) {
        int op,l,r,z; 
        scanf("%d%d%d",&op,&l,&r);  
        if(op==1) scanf("%d",&z),ADD(1,n,1,l,r,z);
        if(op==2) scanf("%d",&z),upmax(1,n,1,l,r,z);
        if(op==3) scanf("%d",&z),upmin(1,n,1,l,r,z);
        if(op==4) printf("%lld\n",qsum(1,n,1,l,r));
        if(op==5) printf("%d\n",qmax(1,n,1,l,r)); 
        if(op==6) printf("%d\n",qmin(1,n,1,l,r));
    }   
    return 0;   
}

例题：洛谷P6242 【模板】线段树 3

不考虑求区间历史最值，和前面的做法一样.

在前面的问题中，出于简化问题的考虑，只维护了一个加法标记.

而实际上，如果子区间的最大值大于父区间最大值，我们还会减掉一部分.

这其实就是相当于对最大值和非最大值都维护了一个区间加法标记.

在本题中，也采用同样的方法，对最大值和非最大值都维护区间加法标记.

对于历史最值，更新方法还是 $\mathrm{mx=max(mx, mx'+tag')}$.

即历史最值的构成方式就是当前标记+历史最大标记.

#include <cstdio>
#include <cmath> 
#include <set>
#include <cstring>
#include <algorithm>
#define N 500009 
#define ll long long
#define pb push_back
#define ls now<<1 
#define rs now<<1|1  
#define setIO(s) freopen(s".in","r",stdin) 
using namespace std; 
const int inf=(int)1e9;  
ll sum[N<<2];   
int add1[N<<2],add2[N<<2],add3[N<<2],add4[N<<2];  
int mx[N<<2],mxp[N<<2],se[N<<2],cnt[N<<2],A[N],n,m,len[N<<2]; 
void pushup(int now) {
    sum[now]=sum[ls]+sum[rs];   
    mxp[now]=max(mxp[ls], mxp[rs]);  
    if(mx[ls] > mx[rs]) {
        mx[now]=mx[ls], cnt[now]=cnt[ls];  
        se[now]=max(se[ls], mx[rs]);    
    }
    else if(mx[ls] < mx[rs]) {
        mx[now]=mx[rs], cnt[now]=cnt[rs];  
        se[now]=max(se[rs], mx[ls]); 
    }
    else {
        se[now]=max(se[ls], se[rs]);  
        mx[now]=mx[ls]; 
        cnt[now]=cnt[ls]+cnt[rs];  
    }
}  
// k1: 最大值加法
// k2: 历史最大值加法.   
// k3: 其他加法
// k4: 其他最大值加法.
void update(int now,int k1,int k2,int k3,int k4) {
    sum[now]+=1ll*k1*cnt[now]+1ll*(len[now]-cnt[now])*k3;
    mxp[now]=max(mxp[now], mx[now]+k2);
    mx[now]+=k1;
    if(se[now]!=-inf) se[now]+=k3;   
    add2[now]=max(add2[now], add1[now]+k2);
    add1[now]+=k1; 
    add4[now]=max(add4[now], add3[now]+k4); 
    add3[now]+=k3;   
}    
void pushdown(int now) {
    int tmp=max(mx[ls], mx[rs]); 
    if(mx[ls]==tmp) {
        // 左边有最大值.  
        update(ls, add1[now], add2[now], add3[now], add4[now]); 
    }
    else {
        update(ls, add3[now], add4[now], add3[now], add4[now]); 
    }
    if(mx[rs]==tmp) {
        update(rs, add1[now], add2[now], add3[now], add4[now]); 
    }
    else {
        update(rs, add3[now], add4[now], add3[now], add4[now]); 
    }
    add1[now]=add2[now]=add3[now]=add4[now]=0; 
}
// 将 [L, R] += v; 
void update1(int l,int r,int now,int L,int R,int v) {
    if(l >= L && r <= R) {
        update(now, v, v, v, v);   
        return ; 
    }
    int mid=(l+r)>>1;  
    pushdown(now);  
    if(L<=mid)  update1(l,mid,ls,L,R,v); 
    if(R>mid)   update1(mid+1,r,rs,L,R,v);  
    pushup(now); 
}
// 将 [L, R] 与 v 取 min.  
void update2(int l,int r,int now,int L,int R,int v) {
    if(mx[now] <= v) return ;   
    if(l>=L&&r<=R&&v>se[now]) {
        update(now, v-mx[now], v-mx[now], 0, 0);
        return ; 
    }
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid)  update2(l,mid,ls,L,R,v); 
    if(R>mid)   update2(mid+1,r,rs,L,R,v);  
    pushup(now); 
}
ll query3(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) {
        return sum[now]; 
    }
    pushdown(now); 
    ll re = 0ll; 
    int mid=(l+r)>>1; 
    if(L<=mid)  re += query3(l, mid, ls, L, R);  
    if(R>mid)   re += query3(mid+1,r,rs,L,R);  
    return re; 
}
int query4(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) {
        return mx[now]; 
    }
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid&&R>mid)  return max(query4(l,mid,ls,L,R), query4(mid+1,r,rs,L,R));  
    else if(L<=mid)    return query4(l,mid,ls,L,R);  
    else return query4(mid+1,r,rs,L,R);   
}
int query5(int l,int r,int now,int L,int R) {
    if(l>=L&&r<=R) {
        return mxp[now]; 
    }
    pushdown(now); 
    int mid=(l+r)>>1;  
    if(L<=mid&&R>mid)  return max(query5(l,mid,ls,L,R), query5(mid+1,r,rs,L,R));  
    else if(L<=mid)    return query5(l,mid,ls,L,R);  
    else return query5(mid+1,r,rs,L,R);   
}
void build(int l,int r,int now) {
    len[now]=r-l+1;  
    if(l==r) {
        mxp[now]=mx[now]=A[l];   
        sum[now]=A[l], se[now]=-inf, cnt[now]=1;      
        return ; 
    }
    int mid=(l+r)>>1; 
    build(l, mid, ls), build(mid+1, r, rs); 
    pushup(now); 
} 
int main() {
    // setIO("input"); 
    scanf("%d%d",&n,&m); 
    for(int i=1;i<=n;++i) {
        scanf("%d",&A[i]); 
    }
    build(1, n, 1); 
    for(int i=1;i<=m;++i) {
        int op,l,r,z;  
        scanf("%d%d%d",&op,&l,&r); 
        if(op==1) scanf("%d",&z),update1(1,n,1,l,r,z);  
        if(op==2) scanf("%d",&z),update2(1,n,1,l,r,z); 
        if(op==3) printf("%lld\n",query3(1,n,1,l,r));  
        if(op==4) printf("%d\n",query4(1,n,1,l,r));  
        if(op==5) printf("%d\n",query5(1,n,1,l,r)); 
    }
    return 0; 
}

posted @ 2021-09-09 01:59 guangheli 阅读(122) 评论(0) 收藏举报

刷新页面返回顶部

guangheli

segment tree beats