第一次作业，深度学习基础

深度学习

第一周的视频课程主要是对深度学习宏观上的介绍，从一些关键时间节点、代表人物、代表技术、专业术语等方面来介绍深度学习的基本功能、优缺点等。

1、视频学习

1.1

1、人工智能是是一部机器像人一样感知、认知、决策、执行的人工程序或系统。

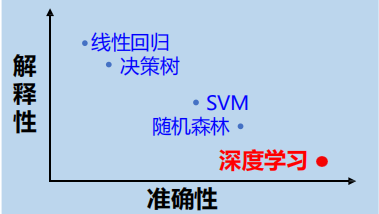
2、人工智能，机器学习，深度学习三者的关系。

1、深度学习的不能

（1）算法不稳定，容易被“攻击”。（2）模型复杂度高，不容易纠错。（3）端到端训练方式对数据依赖性强，模型增量性差。（4）专注于直观感知类问题，对开放型推力问题无能为。

（5）人类知识无法有效引入监督，不可避免的存在偏见与歧视。

2、通过举了一个非常有趣的“狗屎检测”的例子来比较了传统机器学习与深度学习的处理过程，深度学习要效率的多。

3、一切的开始是感知器的提出。感知器是由 Rosenblatt于1957年提出。但是Rosenblatt认为感知器将无所不能，而Minsky则认为感知器的应用是有限的。

4、单层感知器神经网络无法解决不可线性划分的问题，如异或门。

5、辛顿与David Rumelhard合作发表论文，阐述了BP算法及应用：

（1）BP算法通过在神经网络里增加了一个所谓的隐层，解决了异或问题

（2）使用BP算法的神经网络在做如形状识别之类的简单工作时，效率比感知器大大提高。

  从此神经网络开始复苏。

6、Yann lecun使用了“卷积神经网络”的技术。

7、辛顿将“神经网络”改名为“深度学习”。

8、吴恩达等：使用GPU的运算速度和传统双核CPU相比，最快时要快近70倍。

9、SVM：是一类按监督学习方式对数据进行二元分类的广义线性分类器，其决策边界是对学习样本求解的最大边距超平面。

10、Bengio等使用RELU激励函数，对于特定的输入，统计上有一半神经元是没有反应的，保持沉默。RELU函数和别的激励函数模型相比，识别错误率更低，而且其有效性，对于神经网络是否进行“预先训练”过并不敏感。

11、神经网络的三起三落。

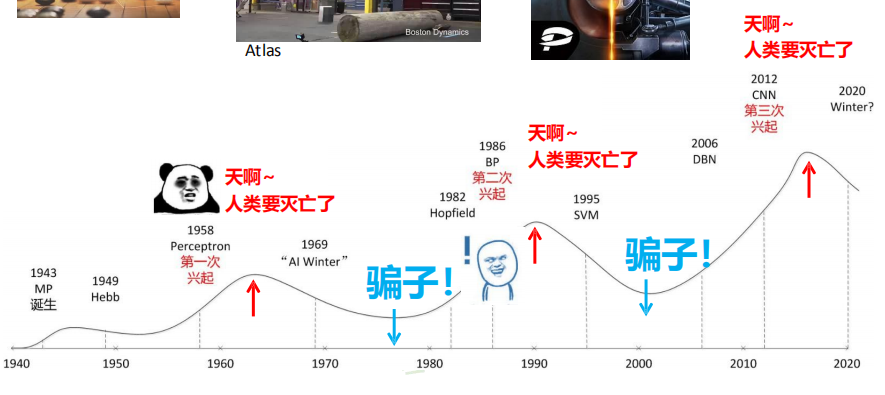
14、

1.2

1、

                                    生物神经元                                                                                                                             M-P神经元

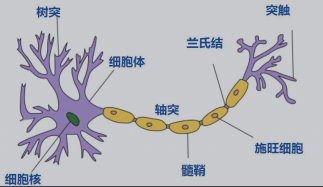
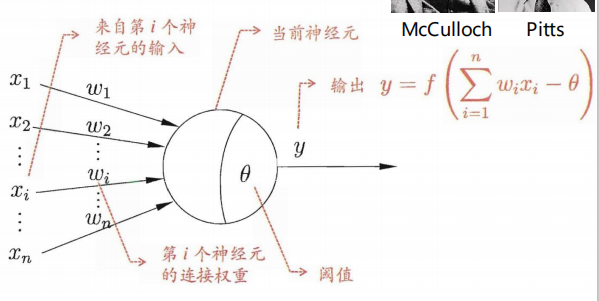
生物神经元	M-P神经元
多输入单输出	多输入信号进行累加∑ixi
空间整合	多输入信号进行累加∑ixi
兴奋性/抑制性输入	权值wi正负模拟兴奋\抑制，大小模拟强度
阈值特性	输入和超过阈值θ，神经元被激活

2、激活函数f:神经元继续传递信息，产生新连接的概率（超过阈值被激活，但不一定传递）

3、激活函数举例：

注：二分类一般采用sigmoid函数。

4、单层感知器是首个可以学习的人工神经网络。

5、单层感知器：非线性激活函数 0 和 1 与或非。

6、多层感知器：三层感知器实现同或。

7、神经网络每一层的作用

每一层数学公式y⃗ =a(W⋅x⃗ +b)

完成输入->输出空间变换

作用 公式参数

升/降维     W·x

放大/缩小 W·x

旋转     W·x

平移 +b

弯曲 a(·)

神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。

增节点数：增加维度，即增加线性转换能力

增加层数：增加激活函数的次数即增加非线性转换次数

8、更深的网络

在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力，产生更多的线性区域。

深度和宽度对函数复杂度的贡献是不同的，深度的共享是指数增长的，而宽度的贡献是线性的。

9、梯度：

多元函数f(x,y)在每个点有多个方向，每个方向都可以计算导数，称为方向导数。

梯度是一个向量：

方向是最大方向导数的方向

模为方向导数的最大值

10、无约束优化：梯度下降

参数沿负梯度方向更新可以使函数值下降。

11、深层神经网络的问题：梯度消失

增加深度会造成梯度消失，误差无法传播，同时多层网络容易陷入局部极值，难以训练。

三层神经网络是主流。

12、深度学习使用两个优化器：Adam和SGD

一般来说Adam效果较好。

13、神经网络的第二次落

 

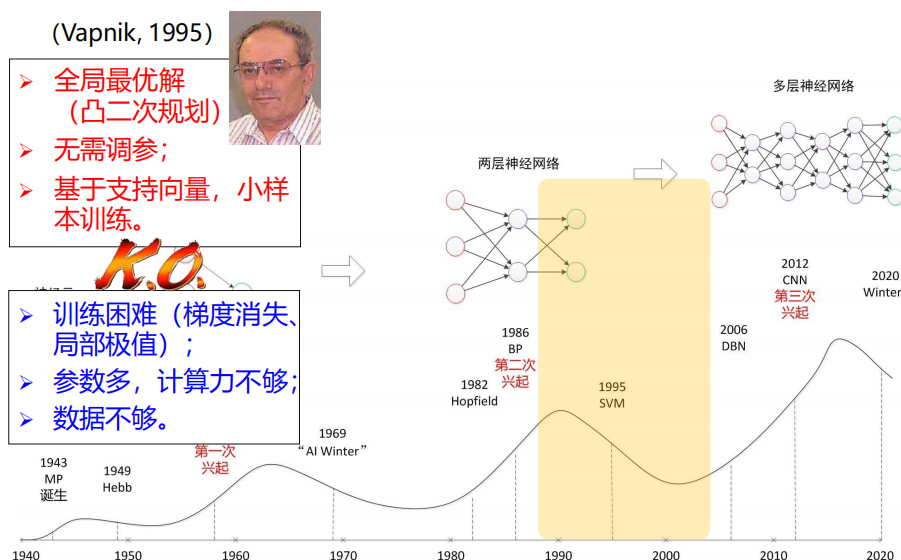
14、神经网络的第三次起

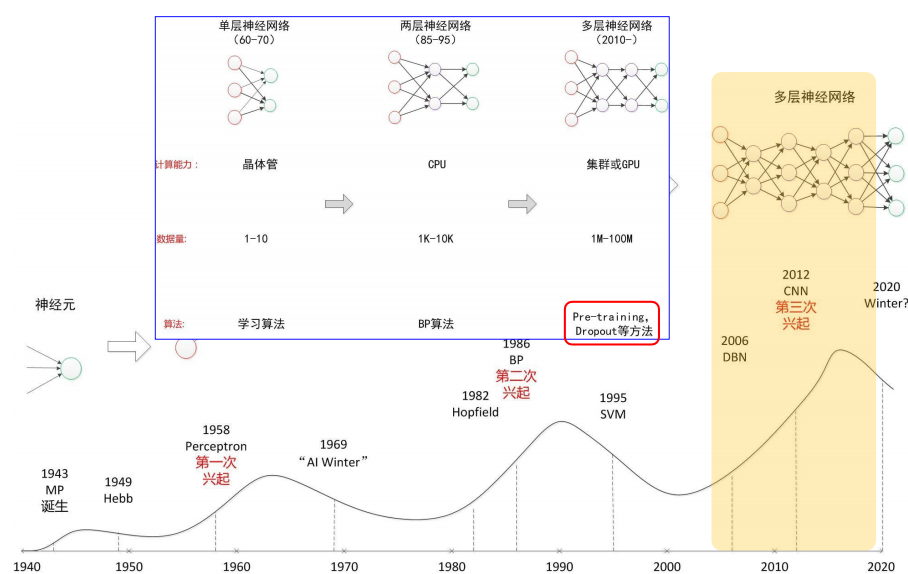
15、自编码器

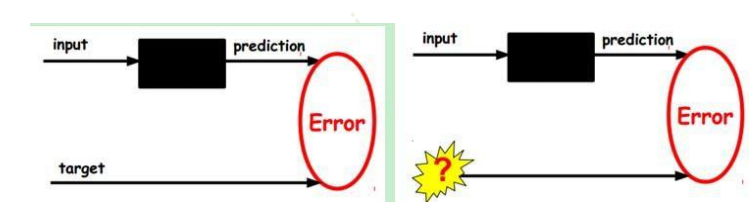
（1）自编码器假设 输出与输入相同，是一种尽可能复现输入信号的神经网络。

将input输入一个encoder编码器，就会得到一个code；加一个decoder解码器输出信息。

通过调整encoder和decoder的参数，使得重构误差最小

没有额外监督信息，无标签数据，误差的来源是直接重构后的信号与原输入相比得到。

（2）自编码器一般是个多层神经网络，最简单是三层：输入层，隐层，输出层。

（1）最初被提出用来降维。

16、堆叠自编码器

将多个自编码器得到的隐层串联

所有顶层预训练完成后，进行基于监督学习的全网络微调

17、解决梯度消失

（1）Layer-wise Pre-train: 2006年Hinton等提出的训练深度网路的方法，用无监督数据作分层预训练，再用有监督数据fine-tume

（2）ReLU:新的激活函数解析性质更好，克服了sigmoid函数和tanh函数的梯度消失问题

（3）辅助损失函数: e.g. GoogLeNet中的两个辅助损失函数，对浅层神经元直接传递梯度

（4）Batch Normalization: 逐层的尺度归一   

2、代码练习

2.1图像处理

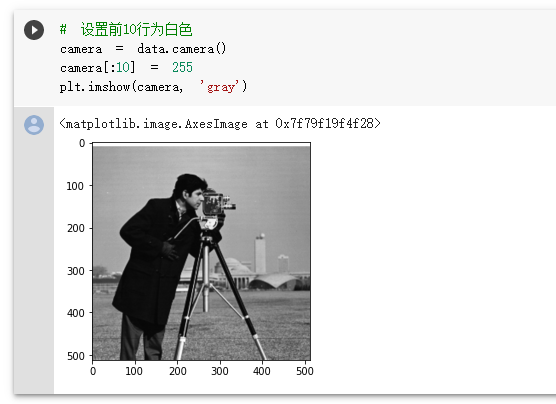
设置一块白色的区域

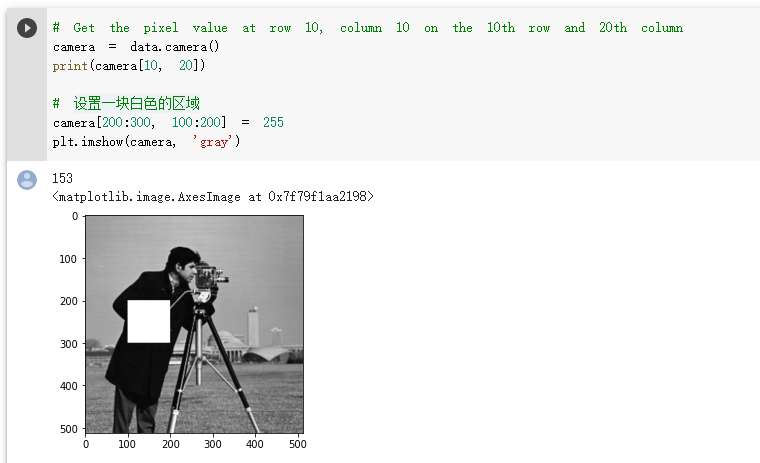
设置前10行为白色

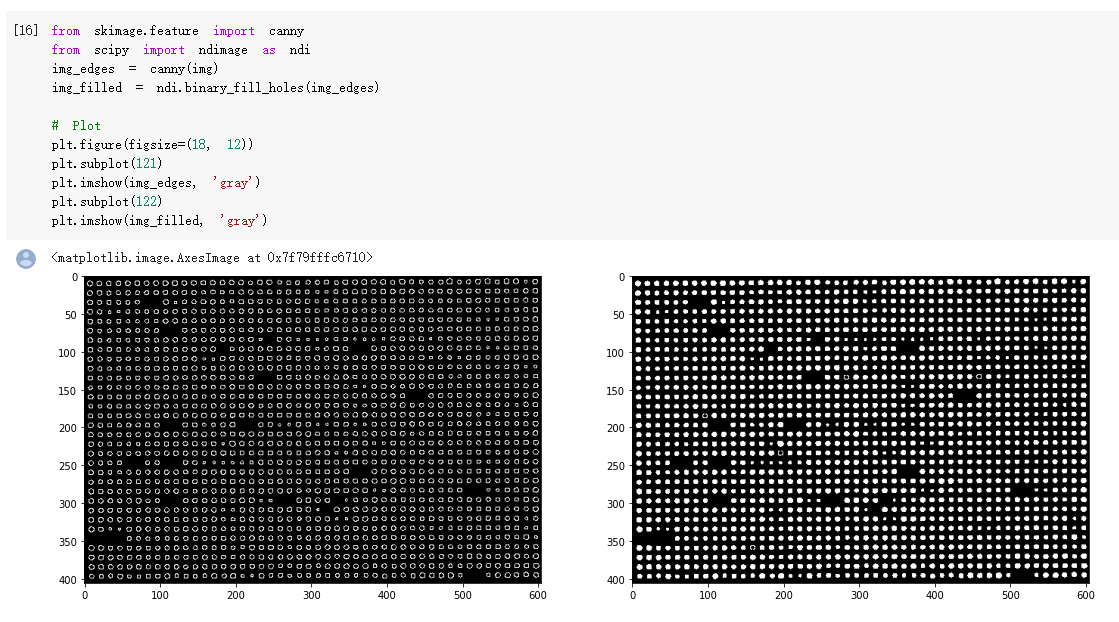
Canny算子用于边缘检测

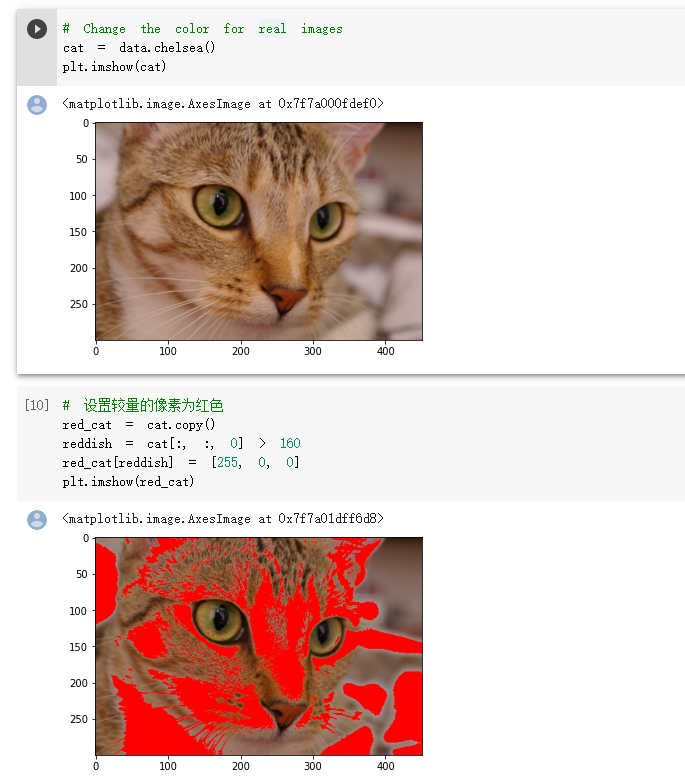
转换图像数据类型

设置较亮的像素为红色

2.2 PyTorch基础

什么是 PyTorch ?

在第三个学习视频中老师也提到过：

PyTorch是一个python库，它主要提供了两个高级功能：1、GPU加速的张量计算

2、构建在反向自动求导系统上的深度神经网络

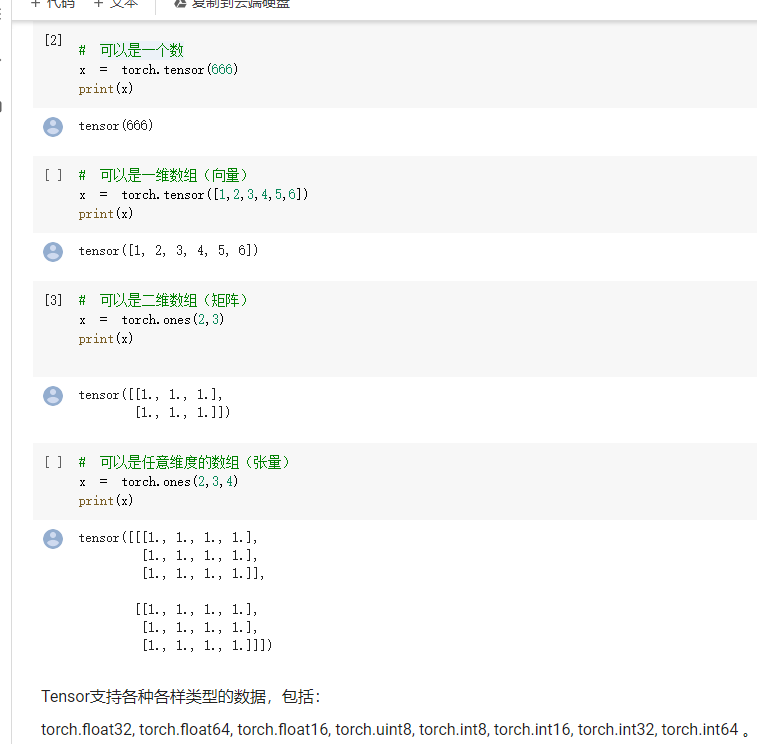
一般定义数据使用torch.Tensor ， tensor的意思是张量，是各种数据的总称

定义数据：张量类 torch.Tensor 任意类型的数据

定义数据操作：函数类 torch.autograd.Function

凡是用torch进行的操作都是Function：基本运算、布尔运算、线性运算等。

Tensor三个重要组成：data（存数据）、grad（存梯度）、grad_fn（用来指向创造自己的Function）

PyTorch里没有一个显式的graph的定义，计算步骤，存在Tensor的grad_fn里沿着Tensor的grad_fn往后走，就是反向传播

2.3 螺旋数据分类

#数据初始化

import random

import torch

from torch import nn, optim

import math

from IPython import display

from plot_lib import plot_data, plot_model, set_default

# 因为colab是支持GPU的，torch 将在 GPU 上运行

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# 初始化随机数种子。神经网络的参数都是随机初始化的，# 不同的初始化参数往往会导致不同的结果，当得到比较好的结果时我们通常希望这个结果是可以复现的，# 因此，在pytorch中，通过设置随机数种子也可以达到这个目的

seed = 12345

random.seed(seed)

torch.manual_seed(seed)

 

N = 1000  # 每类样本的数量

D = 2  # 每个样本的特征维度

C = 3  # 样本的类别

H = 100  # 神经网络里隐层单元的数量

X = torch.zeros(N * C, D).to(device)

Y = torch.zeros(N * C, dtype=torch.long).to(device)

for c in range(C):

    index = 0

    t = torch.linspace(0, 1, N) # 在[0，1]间均匀的取10000个数，赋给t

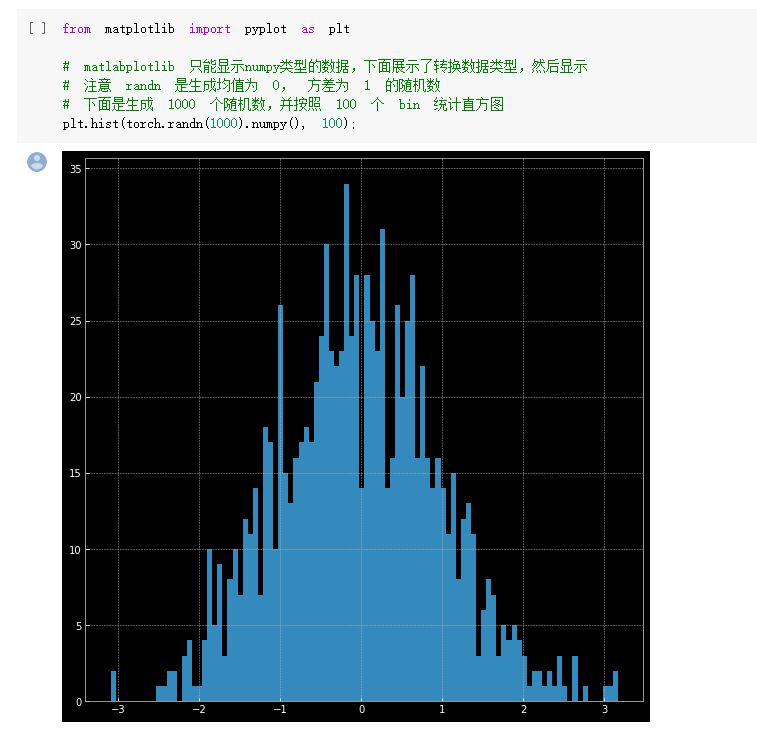
    # 下面的代码不用理解太多，总之是根据公式计算出三类样本（可以构成螺旋形）

    # torch.randn(N) 是得到 N 个均值为0，方差为 1 的一组随机数，注意要和 rand 区分开

    inner_var = torch.linspace( (2*math.pi/C)*c, (2*math.pi/C)*(2+c), N) + torch.randn(N) * 0.2

    

    # 每个样本的(x,y)坐标都保存在 X 里

    # Y 里存储的是样本的类别，分别为 [0, 1, 2]

    for ix in range(N * c, N * (c + 1)):

        X[ix] = t[index] * torch.FloatTensor((math.sin(inner_var[index]), math.cos(inner_var[index])))

        Y[ix] = c

        index += 1

#创建线性模型

learning_rate = 1e-3

lambda_l2 = 1e-5

# nn 包用来创建线性模型# 每一个线性模型都包含 weight 和 bias

model = nn.Sequential(

    nn.Linear(D, H),

    nn.Linear(H, C)

)

model.to(device) # 把模型放到GPU上

# nn 包含多种不同的损失函数，这里使用的是交叉熵（cross entropy loss）损失函数

criterion = torch.nn.CrossEntropyLoss()

# 这里使用 optim 包进行随机梯度下降(stochastic gradient descent)优化

optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate, weight_decay=lambda_l2)

# 开始训练

for t in range(1000):

    # 把数据输入模型，得到预测结果

    y_pred = model(X)

    # 计算损失和准确率

    loss = criterion(y_pred, Y)

    score, predicted = torch.max(y_pred, 1)

    acc = (Y == predicted).sum().float() / len(Y)

    print('[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f' % (t, loss.item(), acc))

    display.clear_output(wait=True)

 

    # 反向传播前把梯度置 0

    optimizer.zero_grad()

    # 反向传播优化

    loss.backward()

    # 更新全部参数

    optimizer.step()

#效果图如下 

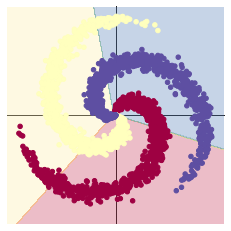
#加入ReLU激活函数

learning_rate = 1e-3

lambda_l2 = 1e-5

# 这里可以看到，和上面模型不同的是，在两层之间加入了一个 ReLU 激活函数

model = nn.Sequential(

    nn.Linear(D, H),

    nn.ReLU(),

    nn.Linear(H, C)

)

model.to(device)

# 下面的代码和之前是完全一样的，这里不过多叙述

criterion = torch.nn.CrossEntropyLoss()

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate, weight_decay=lambda_l2) # built-in L2

# 训练模型，和之前的代码是完全一样的

for t in range(1000):

    y_pred = model(X)

    loss = criterion(y_pred, Y)

    score, predicted = torch.max(y_pred, 1)

    acc = ((Y == predicted).sum().float() / len(Y))

    print("[EPOCH]: %i, [LOSS]: %.6f, [ACCURACY]: %.3f" % (t, loss.item(), acc))

    display.clear_output(wait=True)

    

    optimizer.zero_grad()

    loss.backward()

    optimizer.step()

#效果图如下

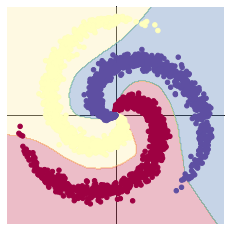
加入ReLU激活函数后，明显比之前分类清晰了许多，使神经网络具备了分层的非线性映射学习能力。

 

2.4 回归分析

 

 

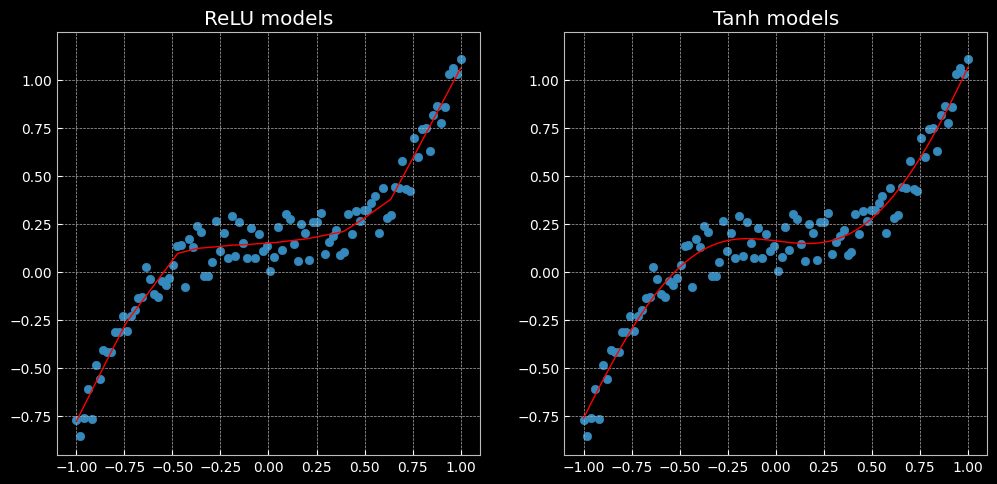
总结：这是以一次接触深度学习，比较吃累，对一切比较陌生，入门较困难，需要再多花时间慢慢的去消化，多向优秀的同学学习。