位操作以及实际应用

位操作是程序设计中对位模式或二进制数的一元和二元操作。

基本的位操作符有  与 & 、或 | 、异或 ^ 、取反 ~ 、左移 << 、右移 >> 这6种。运算规则如下：

 

符号	描述	运算规则
&	与	两个位都为 1 时，结果才为 1
|	或	两个位都为 0 时，结果才为 0
^	异或	两个位相同为 0 ，相异为 1
~	取反	0 变 1 ， 1 变 0
<<	左移	各二进位全部左移若干位，高位丢弃，低位补 0
>>	右移	各二进位全部右移若干位，对无符号数，高位补 0 ，有符号数， 各编译器处理方法不一样，有的补符号位（算术右移），有的补 0 （逻辑右移）

优先级别由高到低：取反 ~ , 与 & , 异或 ^ , 或 |

位操作的简单使用

• 使用取反 ~ 来获取负数：  ~3 + 1
• 使用与&判断奇偶： 16 & 0x1
• 使用异或 ^ 交换两个变量的值：a = a^b;b=a^b;a=a^b;
• 使用或 | 来同时使用多个选项：option1 | option2 | option3
• 使用 << 来向左偏移位, 比如 3 << 0x2 相当于 3 * (2 ^ 2) = 3 * 4 = 12
• 使用 >> 来向右偏移位, 比如 12>> 0x2 相当于 12 / (2 ^ 2) = 12 / 4 = 3

java位运算在程序设计中的使用：位掩码（BitMask）

例如，在一个系统中，用户一般有查询(Select)、新增(Insert)、修改(Update)、删除(Delete)四种权限，四种权限有多种组合方式，也就是有16中不同的权限状态（2的4次方）。

Permission

一般情况下会想到用四个boolean类型变量来保存：

public class Permission{

    //是否允许查询
    private boolean allowSelect;

    //是否允许新增
    private boolean allowInsert;

    //是否允许删除
    private boolean allowDelete;

    //是否允许更新
    private boolean allowUpdate;

    //省略Getter和Setter

}

上面用4个boolean类型变量来保存每种权限状态。

 

NewPermission

下面是另外一种方式，使用位掩码，用一个二进制数即可，每一位来表示一种权限，0 表示无权限 ，1 表示有权限

public class NewPermission {

    // 是否允许查询，二进制第1位，0表示否，1表示是
    public static final int ALLOW_SELECT = 1 << 0; // 0001

    // 是否允许新增，二进制第2位，0表示否，1表示是
    public static final int ALLOW_INSERT = 1 << 1; // 0010

    // 是否允许修改，二进制第3位，0表示否，1表示是
    public static final int ALLOW_UPDATE = 1 << 2; // 0100

    // 是否允许删除，二进制第4位，0表示否，1表示是
    public static final int ALLOW_DELETE = 1 << 3; // 1000

    // 存储目前的权限状态
    private int flag;

    /**
     *  重新设置权限
     */
    public void setPermission(int permission) {
        flag = permission;
    }

    /**
     *  添加一项或多项权限
     */
    public void enable(int permission) {
        flag |= permission;
    }

    /**
     *  删除一项或多项权限
     */
    public void disable(int permission) {
        flag &= ~permission;
    }

    /**
     *  是否拥某些权限
     */
    public boolean isAllow(int permission) {
        return (flag & permission) == permission;
    }

    /**
     *  是否禁用了某些权限
     */
    public boolean isNotAllow(int permission) {
        return (flag & permission) == 0;
    }

    /**
     *  是否仅仅拥有某些权限
     */
    public boolean isOnlyAllow(int permission) {
        return flag == permission;
    }
}

以上代码中，用四个常量表示了每个二进制位代码的权限项。

例如：

ALLOW_SELECT = 1 << 0 转成二进制就是0001，二进制第一位表示Select权限。
ALLOW_INSERT = 1 << 1 转成二进制就是0010，二进制第二位表示Insert权限。

private int flag存储了各种权限的启用和停用状态，相当于代替了Permission中的四个boolean类型的变量。

用flag的四个二进制位来表示四种权限的状态，每一位的0和1代表一项权限的启用和停用，下面列举了部分状态表示的权限：

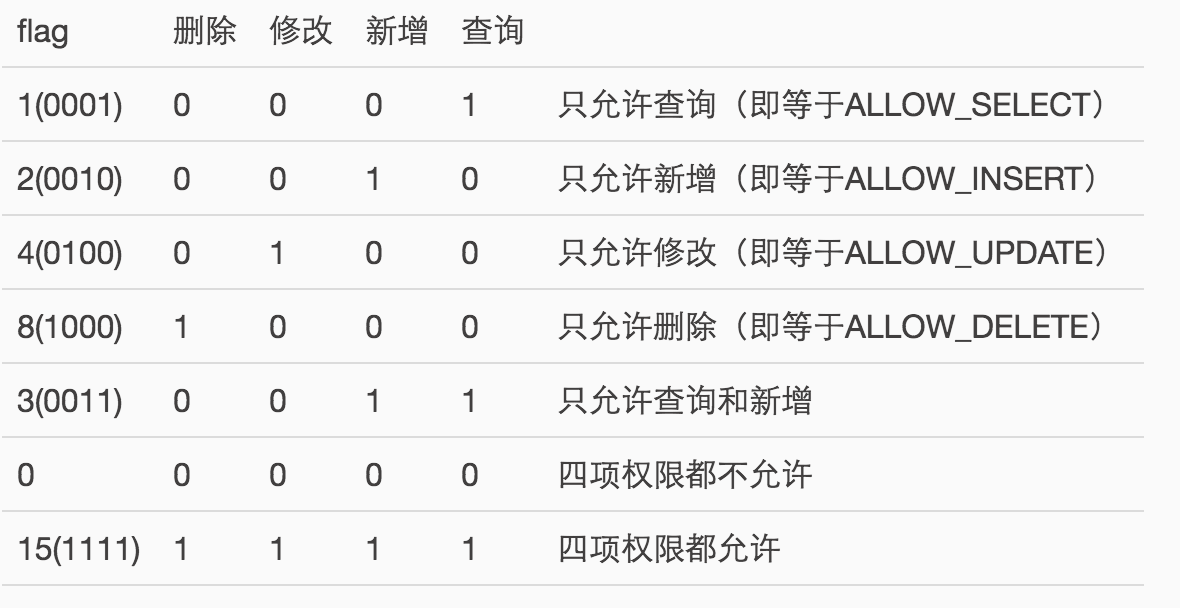
使用位掩码的方式，只需要用一个大于或等于0且小于16的整数即可表示所有的16种权限的状态。

此外，还有很多设置权限和判断权限的方法，需要用到位运算，例如：

public void enable(int permission) {
    flag |= permission; // 相当于flag = flag | permission;
}

调用这个方法可以在现有的权限基础上添加一项或多项权限。

添加一项Update权限：

permission.enable(NewPermission.ALLOW_UPDATE);

假设现有权限只有Select，也就是flag是0001。执行以上代码，flag = 0001 | 0100，也就是0101，便拥有了Select和Update两项权限。

添加Insert、Update、Delete三项权限：

permission.enable(NewPermission.ALLOW_INSERT 
    | NewPermission.ALLOW_UPDATE | NewPermission.ALLOW_DELETE);

NewPermission.ALLOW_INSERT | NewPermission.ALLOW_UPDATE | NewPermission.ALLOW_DELETE运算结果是1110。假设现有权限只有Select，也就是flag是0001。flag = 0001 | 1110，也就是1111，便拥有了这四项权限，相当于添加了三项权限。

上面的设置如果使用最初的Permission类的话，就需要下面三行代码：

permission.setAllowInsert(true);
permission.setAllowUpdate(true);
permission.setAllowDelete(true);

二者对比
设置仅允许Select和Insert权限

Permission

permission.setAllowSelect(true);
permission.setAllowInsert(true);
permission.setAllowUpdate(false);
permission.setAllowDelete(false);

NewPermission

permission.setPermission(NewPermission.ALLOW_SELECT | NewPermission.ALLOW_INSERT);

判断是否允许Select和Insert、Update权限

Permission

if (permission.isAllowSelect() && permission.isAllowInsert() && permission.isAllowUpdate())

NewPermission

if (permission. isAllow (NewPermission.ALLOW_SELECT 
    | NewPermission.ALLOW_INSERT | NewPermission.ALLOW_UPDATE))

判断是只否允许Select和Insert权限

Permission

if (permission.isAllowSelect() && permission.isAllowInsert() 
    && !permission.isAllowUpdate() && !permission.isAllowDelete())

NewPermission

if (permission. isOnlyAllow (NewPermission.ALLOW_SELECT | NewPermission.ALLOW_INSERT))

二者对比可以感受到MyPermission位掩码方式相对于Permission的优势，可以节省很多代码量，位运算是底层运算，效率也非常高，而且理解起来也很简单。

 

一些用到位掩码的源代码
java.lang.reflect.Modifier

在Java反射中，java.lang.reflect.Modifier是用来判断类、成员变量、方法等包含的修饰符。在Modifier的源代码中可以看到：

public static final int PUBLIC           = 0x00000001;
public static final int PRIVATE          = 0x00000002;  
public static final int PROTECTED        = 0x00000004;  
public static final int STATIC           = 0x00000008;  
public static final int FINAL            = 0x00000010;  
public static final int SYNCHRONIZED     = 0x00000020;
// ......
public static boolean isProtected(int mod) {
    return (mod & PROTECTED) != 0;
}
public static boolean isStatic(int mod) {
    return (mod & STATIC) != 0;
}

android.text.util.Linkify

在Android开发中，Linkify可以设置文本中的地址、电话、邮箱等是否支持点击链接：

Linkify.addLinks(textView, Linkify.WEB_URLS | Linkify.EMAIL_ADDRESSES);

android.text.util.Linkify部分源码：

public static final int WEB_URLS = 0x01;
public static final int EMAIL_ADDRESSES = 0x02;
public static final int PHONE_NUMBERS = 0x04;
public static final int MAP_ADDRESSES = 0x08;
public static final int ALL = WEB_URLS | EMAIL_ADDRESSES | PHONE_NUMBERS | MAP_ADDRESSES;

public static final boolean addLinks(Spannable text, int mask) {
    if (mask == 0) {
        return false;
    }

    URLSpan[] old = text.getSpans(0, text.length(), URLSpan.class);

    for (int i = old.length - 1; i >= 0; i--) {
        text.removeSpan(old[i]);
    }

    ArrayList<LinkSpec> links = new ArrayList<LinkSpec>();

    if ((mask & WEB_URLS) != 0) {
        gatherLinks(links, text, Patterns.WEB_URL,
            new String[] { "http://", "https://", "rtsp://" },
            sUrlMatchFilter, null);
    }

    if ((mask & EMAIL_ADDRESSES) != 0) {
        gatherLinks(links, text, Patterns.EMAIL_ADDRESS,
            new String[] { "mailto:" },
            null, null);
    }

    if ((mask & PHONE_NUMBERS) != 0) {
        gatherLinks(links, text, Patterns.PHONE,
            new String[] { "tel:" },
            sPhoneNumberMatchFilter, sPhoneNumberTransformFilter);
    }

    if ((mask & MAP_ADDRESSES) != 0) {
        gatherMapLinks(links, text);
    }

    pruneOverlaps(links);

    if (links.size() == 0) {
        return false;
    }

    for (LinkSpec link: links) {
        applyLink(link.url, link.start, link.end, text);
    }

    return true;
}

 

可以替代位域的更好的方案
在《Effective Java》一书中，更推荐用EnumSet来代替位域：

位域表示法也允许利用位操作，有效的执行像union和intersection这样的集合操作。但位域有着int枚举常量所有的缺点，甚至更多。当位域以数字形式打印时，翻译位域比翻译简单的int枚举常量要困难很多。甚至要遍历位域表示的所有元素也没有很容易的方法。

public class Text {
    public static final int STYLE_BOLD          = 1 << 0;
    public static final int STYLE_ITALIC        = 1 << 1;
    public static final int STYLE_UNDERLINE     = 1 << 2;
    public static final int STYLE_STRIKETHROUGH = 1 << 3;

    public void applyStyles(int styles) {...}
}

调用：

text.applyStyles(STYLE_BOLD | STYLE_ITALIC);

改成EnumSet的写法是：

public class Text {

    public enum Style {
        BOLD, ITALIC, UNDERLINE, STRIKETHROUGH
    }

    public void applyStyles(Set<Style> styles) {
        System.out.println(styles);
    }
}

调用：

text.applyStyles(EnumSet.of(Style.BOLD, Style.ITALIC));

 

位运算面试题

x & (x - 1) 用于消去x最后一位的1

 x = 1100

x - 1 = 1011

x & (x - 1) = 1000

 

 

用 O(1) 时间检测整数 n 是否是 2 的幂次。

思路解析：

N如果是2的幂次，则N满足两个条件。

   1.N >0 

   2.N的二进制表示中只有一个1

因为N的二进制表示中只有一个1，所以使用N & (N - 1)将N唯一的一个1消去，应该返回0。

public class Solution{
    public boolean checkPowerOf2(int n){
        return n>0 && (n&(n-1))==0;  
    }
}

 

 

给出两个32位的整数N和M，以及两个二进制位的位置i和j。写一个方法来使得N中的第i到j位等于M（M会是N中从第i为开始到第j位的子串）。

思路解析：

根据题意，可以有一个想法，将n中第i位到第j位的先置为0，然后，按位或m << i即可。 

现在问题是如何将n中第i位到第j位置为0，可以考虑构造一个数，这个数从第i位到第j位是0，其他位都为1。

这样的数并不是很好构造，所以，我们构造一个数从第i位到第j位都是1，其他位为0的数，然后将这个数取反，就可以得到从第i位到第j位是0，其他位是1的数。

-1的二进制表示是所有位为1，我们以这个数为起点。需要的做的是将高(31-j)位置0，将低i位置0。

将-1先左移(31-j)位，因为高(31-j)位都是不需要的。

然后再将((-1) << (31 -  j))逻辑右移(31 - j + i)位，因为要将低i位置0.

然后再将(((-1) <<(31 - j)) >>> (31 - j + i))左移i位，将1恢复到正确的位置即可。即得到第i位到第j位是1，其他位是0的数。

class Solution{
    public int updateBits(int n,int m, int i , int j){
        return ((~((((-1)<<(31 - j ))>>(31- j + 1))<< i )) & n) | (m << i );
    }
}

 

 

 

给出两个整数a和b, 求他们的和, 但不能使用 + 等数学运算符。

主要利用异或运算来完成，异或运算有一个别名叫做：不进位加法，那么a^b就是a和b相加之后，该进位的地方不进位的结果，然后下面考虑哪些地方要进位，自然是a和b里都是1的地方，a&b就是a和b里都是1的那些位置，a&b<<1就是进位之后的结果。所以a+b=(a^b) + ((a&b)<<1).令a' = a^b,b'=(a&b)<<1可以知道，这个过程是在模拟加法的运算过程，进位不可能一直持续，所以b最终会变为0,。因此重复做上述操作就可以求得a+b的结果。

class Solution{
     public int aplusb(int a, int b){
        while(b != 0){
            int _a = a ^ b;
            int _b = (a & b) << 1;
            a = _a;
            b = _b;
        }
        return a;
    }
}

 

 

 

计算在一个 32 位的整数的二进制表式中有多少个 1。

思路解析：

由x & (x - 1)消去x最后一位的1可知。不断使用 x & (x - 1) 消去x最后一位的1，计算总共消去了多少次即可。

class Solution{
    public int countOnes(int num){
        int count = 0;
        while(num != 0){
            num = num & (num - 1);
            count++;
        }
        return count;
    }
}

 

 

如果要将整数A转换为B，需要改变多少个bit位？

解题思路：

这个应用是上面一个应用的拓展。

思考将整数A转换为B，如果A和B在第i（0<=i<32）个位上相等，则不需要改变这个BIT位，如果在第i位上不相等，则需要改变这个BIT位。所以问题转化为了A和B有多少个BIT位不相同。联想到位运算有一个异或操作，相同为0，相异为1，所以问题转变成了计算A异或B之后这个数中1的个数。

class Solution{
     public int countOnes(int num){
         int count = 0;
         while(num != 0){
             num = num & (num - 1);
             count++;
         }
         return count;
     }
    public int bitSwapRequired(int a , int b){
        return countOnes(a ^ b);
    }
 }

 

 

给定一个含不同整数的集合，返回其所有的子集。

解题思路：

思路就是使用一个正整数二进制表示的第i位是1还是0，代表集合的第i个数取或者不取。

所以从0到2^n-1总共2^n个整数，正好对应集合的2^n个子集。

S = {1,2,3}

N bit Combination
0 000 {}
1 001 {1}
2 010 {2}
3 011 {1,2}
4 100 {3}
5 101 {1,3}
6 110 {2,3}
7 111 {1,2,3}

 

数组中，只有一个数出现一次，剩下都出现两次，找出出现一次的数

思路解析：

因为只有一个数恰好出现一个，剩下的都出现过两次，所以只要将所有的数异或起来，就可以得到唯一的那个数。

 

数组中，只有一个数出现一次，剩下都出现三次，找出出现一次的数

解题思路：

因为数是出现三次的，也就是说，对于每一个二进制位，如果只出现一次的数在该二进制位为1，那么这个二进制位在全部数字中出现次数无法被3整除。

膜3运算只有三种状态：00,01,10，因此我们可以使用两个位来表示当前位%3，对于每一位，我们让Two，One表示当前位的状态，B表示输入数字的对应位，Two+和One+表示输出状态。

0 0 0 0 0

0 0 1 0 1

0 1 0 0 1

0 1 1 1 0

1 0 0 1 0

1 0 1 0 0

One+ = (One ^ B) & (~Two)

Two+ = (~One+) & (Two ^ B)

 

 

数组中，只有两个数出现一次，剩下都出现两次，找出出现一次的数

思路解析：

有了第一题的基本的思路，我们可以将数组分成两个部分，每个部分里只有一个元素出现一次，其余元素都出现两次。那么使用这种方法就可以找出这两个元素了。

不妨假设出现一个的两个元素是x，y，那么最终所有的元素异或的结果就是res = x^y。并且res！=0，那么我们可以找出res二进制表示中的某一位是1。对于原来的数组，我们可以根据这个位置是不是1就可以将数组分成两个部分。x，y在不同的两个子数组中。而且对于其他成对出现的元素，要么在x所在的那个数组，要么在y所在的那个数组。