Tarjan 学习笔记

1.前置知识

• 强联通：若两个点可以互相通达，则称这两个点强联通。

• 强连通图：若图中每两个点都强联通，则称这个图为强连通图。

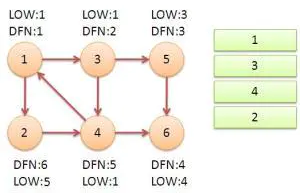
• 强联通分量：若图中有一个子图中每两个点都强连通，则称这个子图为强连通分量。

如图中 \(\{1,2,3,4\}\)、\(\{5\}\)、\(\{6\}\) 即为强连通分量

• 链式前向星

可以阅读https://blog.csdn.net/sugarbliss/article/details/86495945。

2.Tarjan

Tarjan是一种用来求强连通分量的算法。

我们用一个数组 \(dfn\) 来存当前点的编号，用一个数组 \(low\) 来存当前点能到达的点的最小编号，用一个数组 \(vis\) 来表示当前点是否被访问过。

然后进行 \(\texttt{DFS}\)。每遍历到一个点就让它入栈，并且把 \(vis_{i}\) 赋为 \(\texttt{true}\)，表示当前点被遍历过且在栈内。

如果下一个要遍历的点没被遍历过，那么先遍历下一个点，然后把当前的 \(low_{i}\) 更新为 \(\min(low_{i},low_{r[i]})\)。（\(r_{i}\) 表示下一个要遍历的点）

如果下一个要遍历的点被遍历过且还在栈内，那么把当前的 \(low_{i}\) 更新为 \(\min(low_{i},dfn_{r[i]})\)。

举个例子，如图。

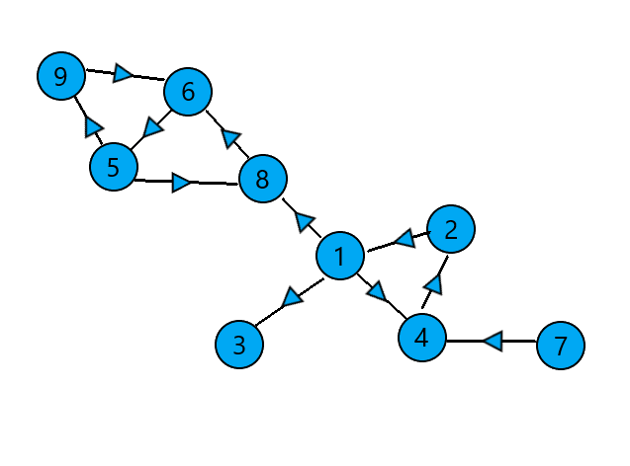
从\(1\)开始 \(\texttt{DFS}\)，将 \(1\) 入栈，\(dfn_{1}=1,low_{1}=1\)。

\(\texttt{DFS}\) \(3\)，未被遍历过，将 \(3\) 入栈，\(dfn_{3}=2,low_{3}=2\)。

\(3\) 不能继续 \(\texttt{DFS}\)，将 \(3\) 出栈。

\(\texttt{DFS}\) \(4\)，未被遍历过，将 \(4\) 入栈，\(dfn_{4}=3,low_{4}=3\)。

\(\texttt{DFS}\) \(2\)，未被遍历过，将 \(2\) 入栈，\(dfn_{2}=4,low_{2}=4\)。

\(\texttt{DFS}\) \(1\)，已被遍历，\(low_{2}=\min(low_{2},dfn_{1})=1\)。

返回 \(4\)，\(low_{4}=1\)。

返回 \(1\)。

\(\texttt{DFS}\) \(8\)，未被遍历过，将 \(8\) 入栈，\(dfn_{8}=5,low_{8}=5\)。

\(\texttt{DFS}\) \(6\)，未被遍历过，将 \(6\) 入栈，\(dfn_{6}=6,low_{6}=6\)。

\(\texttt{DFS}\) \(5\)，未被遍历过，将 \(5\) 入栈，\(dfn_{5}=7,low_{5}=7\)。

\(\texttt{DFS}\) \(9\)，未被遍历过，将 \(9\) 入栈，\(dfn_{9}=8,low_{9}=8\)。

\(\texttt{DFS}\) \(6\)，已被遍历，\(low_{9}=\min(low_{9},dfn_{6})=6\)。

返回 \(5\)。

返回 \(6\)，\(low_{6}=5\)。

返回 \(8\)。

\(9\) 出栈。

\(5\) 出栈。

\(6\) 出栈。

\(8\) 出栈。

\(2\) 出栈。

\(4\) 出栈。

\(1\) 出栈。

\(\texttt{DFS}\) \(7\)，未被遍历过，将 \(7\) 入栈，\(dfn_{7}=9,low_{7}=9\)。

\(7\) 出栈。

\(\texttt{tarjan}\) 结束。

如果不懂，可以结合以下动图食用。

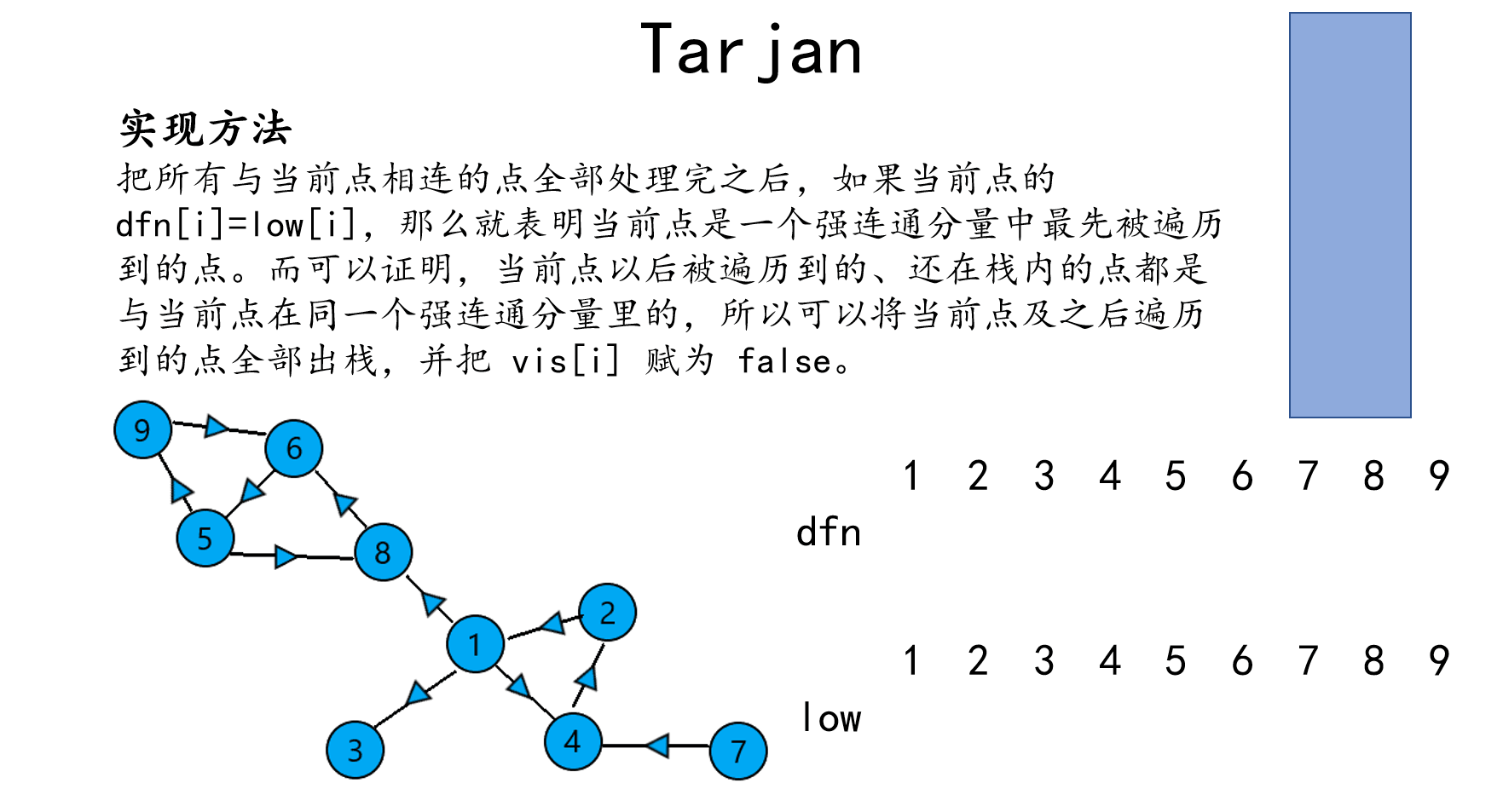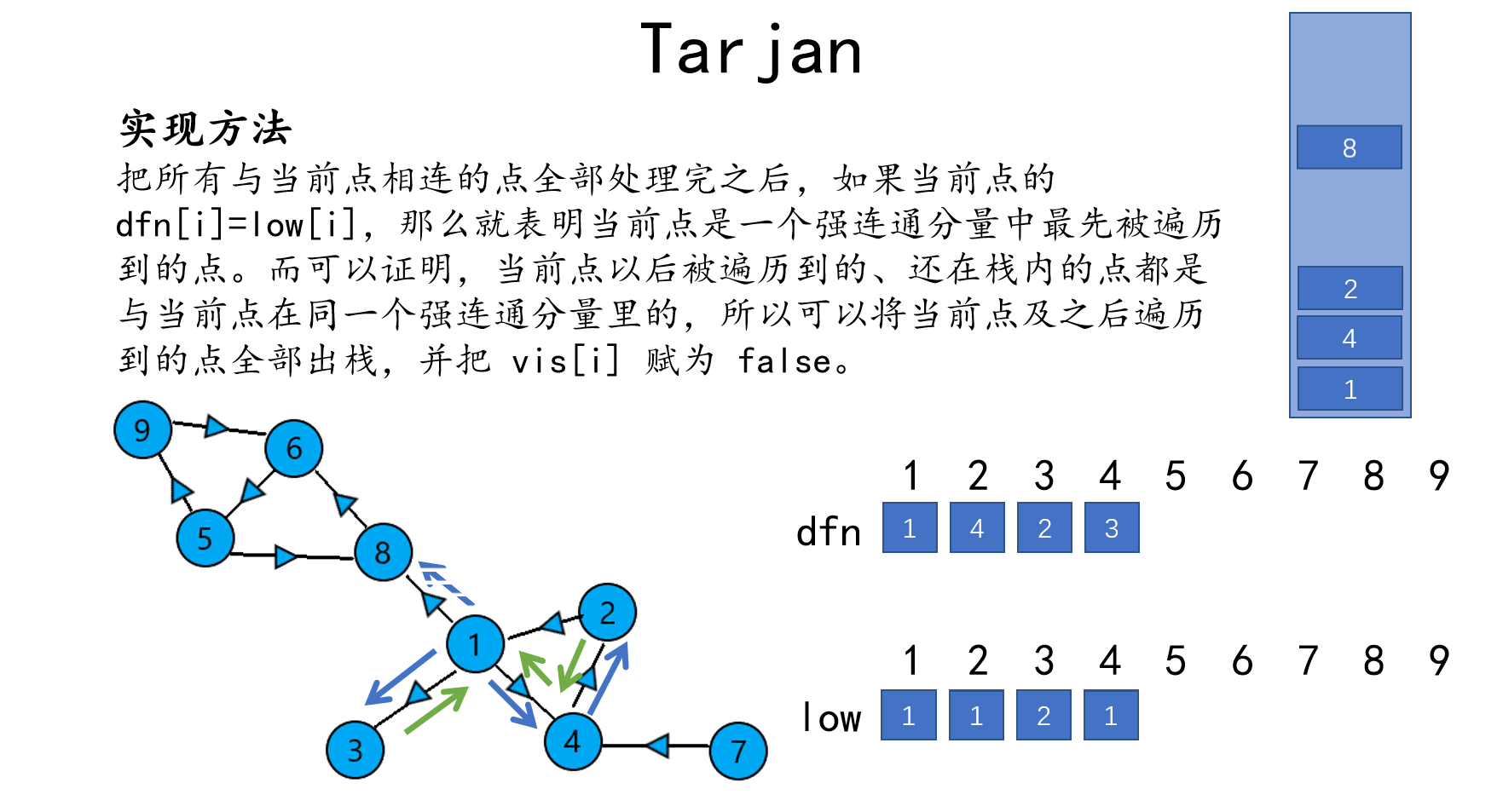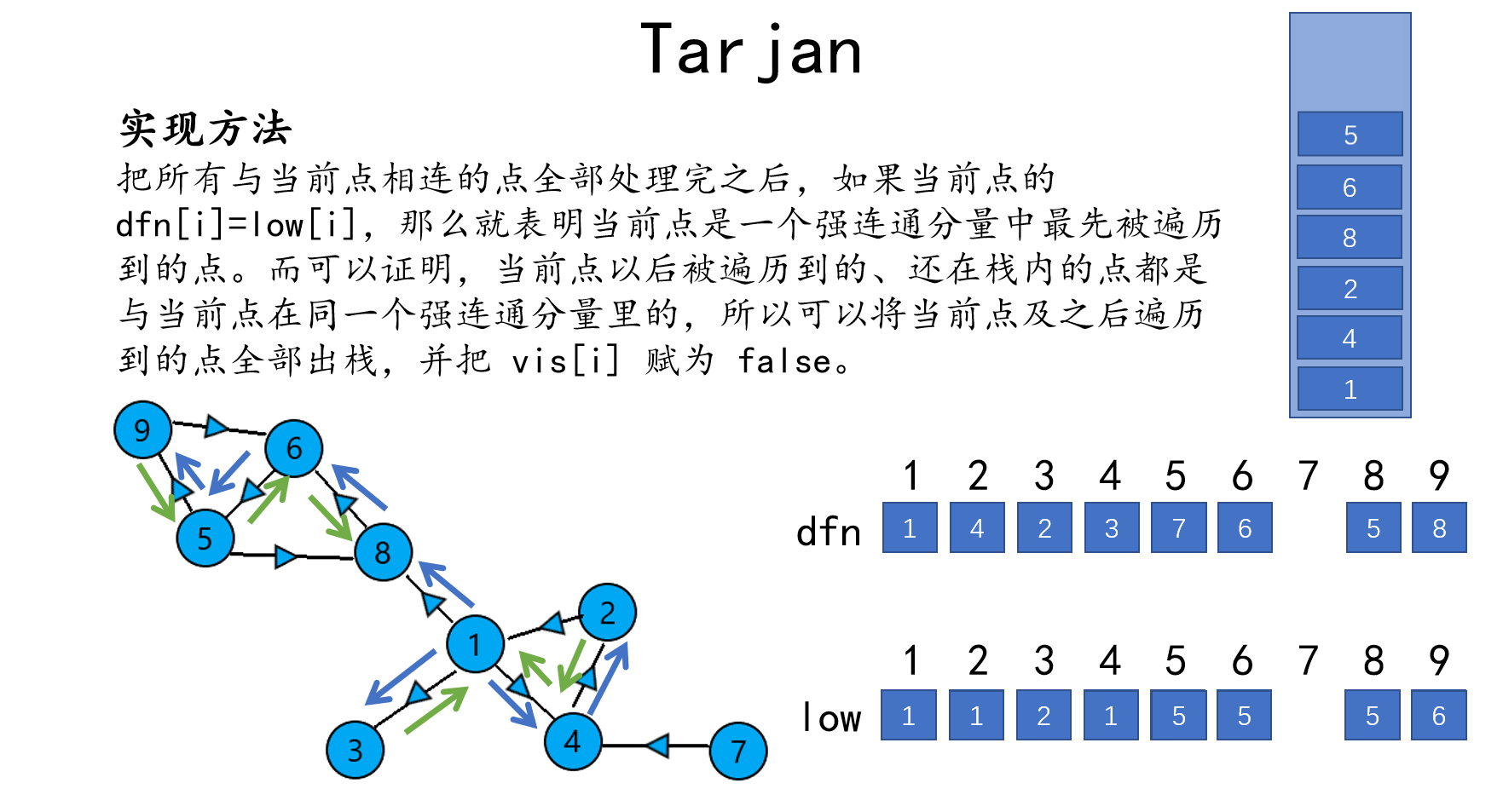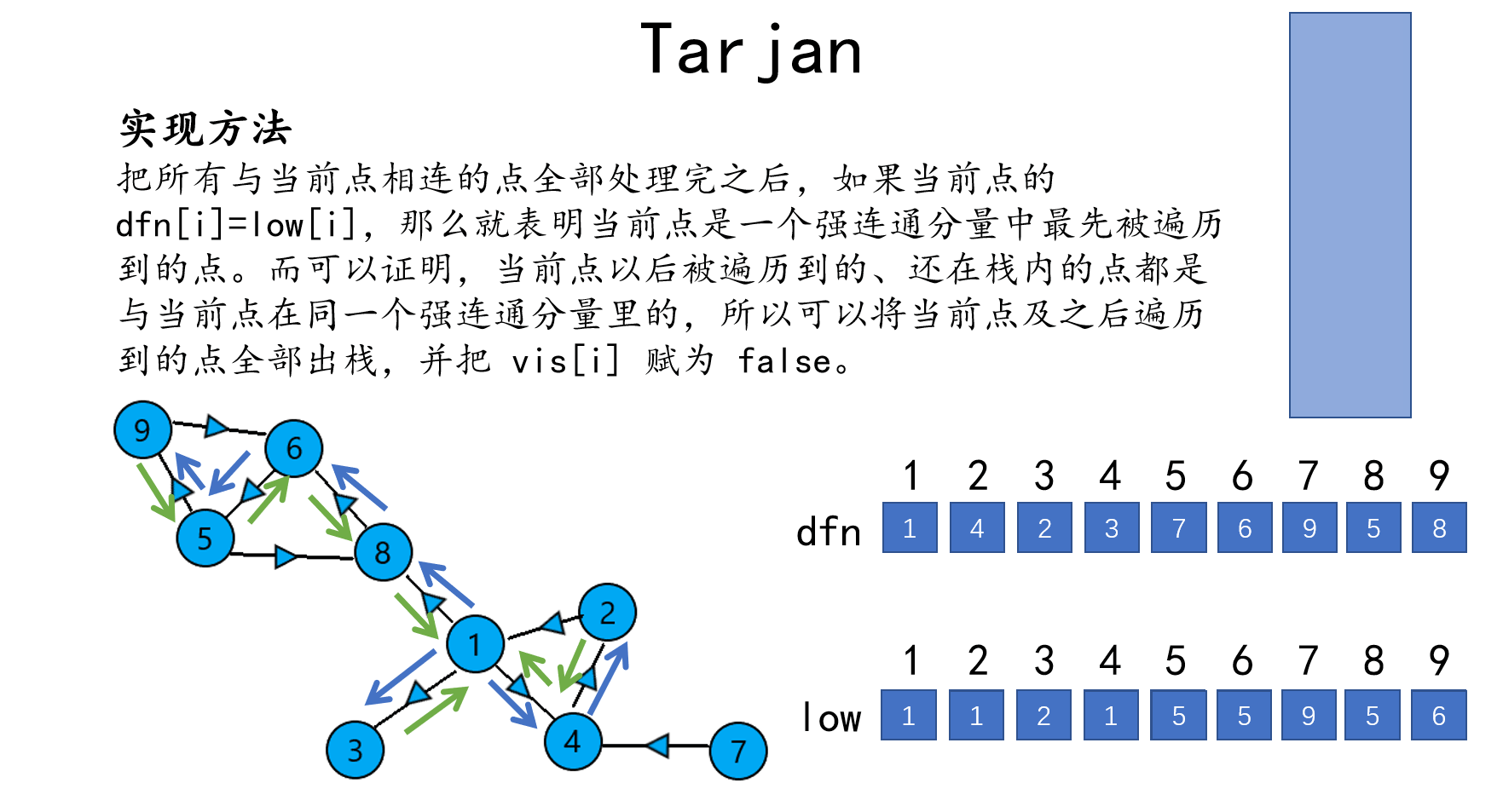
3.总结

例题：P2661。

题意：图中的每一个点都连有一条有向边 \((i,t_{i})\)，求图中最小环。

解答：考虑在 \(\texttt{tarjan}\) 过程中求最小环，如果当前是一个环，则打擂台找最小值，注意排除自环。

#include<bits/stdc++.h>
using namespace std;
int n,ans=0x3ffffff;
int a;
int sta[200002],top;//查询数组
int dfn[200002],low[200002],tot;//tarjan数组
int head[200002],Next[200002],to[200002],cnt;//链式前向星数组
int f[200002];//栈
void addedge(int x,int y)//链式前向星
{
    cnt++;
    Next[cnt]=head[x];
    head[x]=cnt;
    to[cnt]=y;
}
void tarjan(int u)
{
    f[u]=1;//标记为已入栈
    dfn[u]=low[u]=++tot;//记录dfn和low
    sta[++top]=u;//记录，便于查询
    for(int i=head[u];i;i=Next[i])
        if(!dfn[to[i]]) {tarjan(to[i]);low[u]=min(low[u],low[to[i]]);}//如果该点未被访问，则对此点进行tarjan
            else if(f[to[i]]) low[u]=min(low[u],dfn[to[i]]);//否则更新low
    if(low[u]==dfn[u])//如果找到环
    {
        int res=0;
        do
        {
            f[sta[top]]=0;//出栈
            res++;
        }while(sta[top--]!=u);//找出当前环的点数
        if(res!=1) ans=min(ans,res);//寻找最小值
    }
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) {cin>>a;addedge(i,a);}//存图
    for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);//如果该点未被访问，则对此点进行tarjan
    cout<<ans;
    return 0;
}

图论基础。

参考资料：

图论——\(\color{black}O\color{red}RzyzRO\)

https://www.luogu.com.cn/blog/hicc0305/solution-p2661

https://www.jianshu.com/p/346e01244080